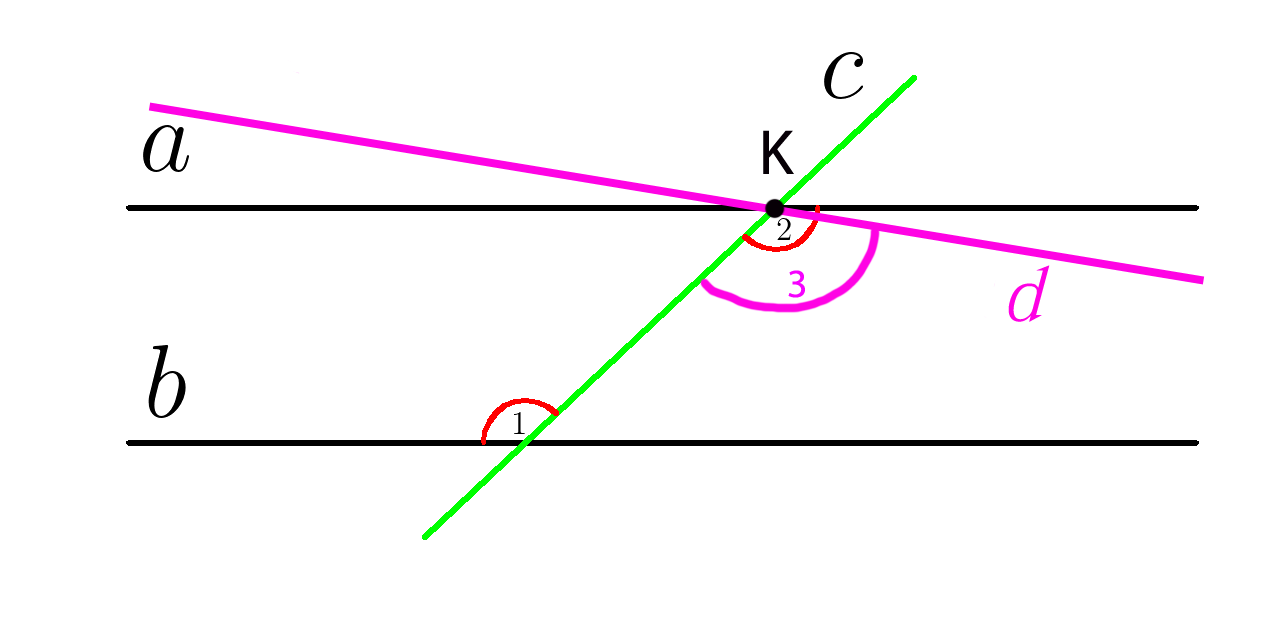
Параллельные прямые и секущая

При пересечении двух параллельных прямых секущей накрест лежащие углы равны
Второй признак равенства треугольников

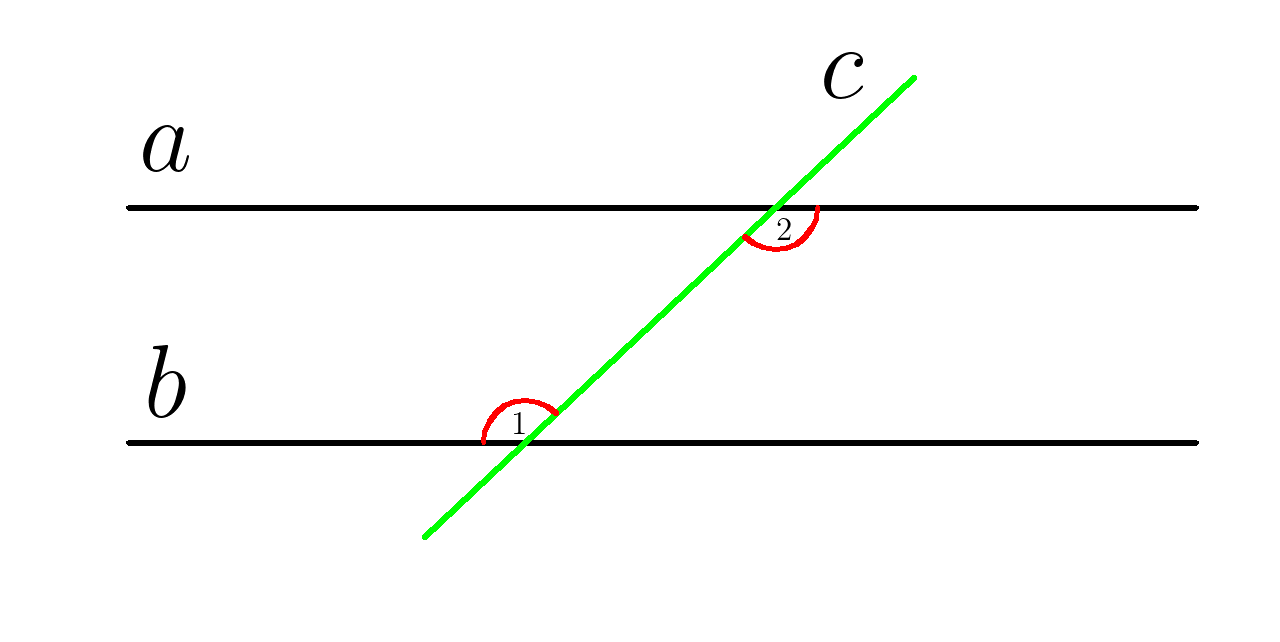
знак \( \left | \right | \) означает параллельность

\( a \; \left | \right | \; b \)

\( \angle 1 = \angle 2 \)

\( \angle 1 и \angle 2 \) - накрест лежащие углы при параллельных прямых \(a и b \) и секущей \(c\)

1. На рисунке \( a \; \left | \right | \; b , \) найти \(\angle 2, \; \)если \( \; \angle 1 = 130^0 \)
Показать ответ Показать решение Видеорешение

Ответ: \(130 \)

\( \angle 2= \angle 1 = 130^0 \) (так как они накрест лежащие при \( a \; \left | \right | \; b \) )

Ответ: 130

ПОЗЖЕ

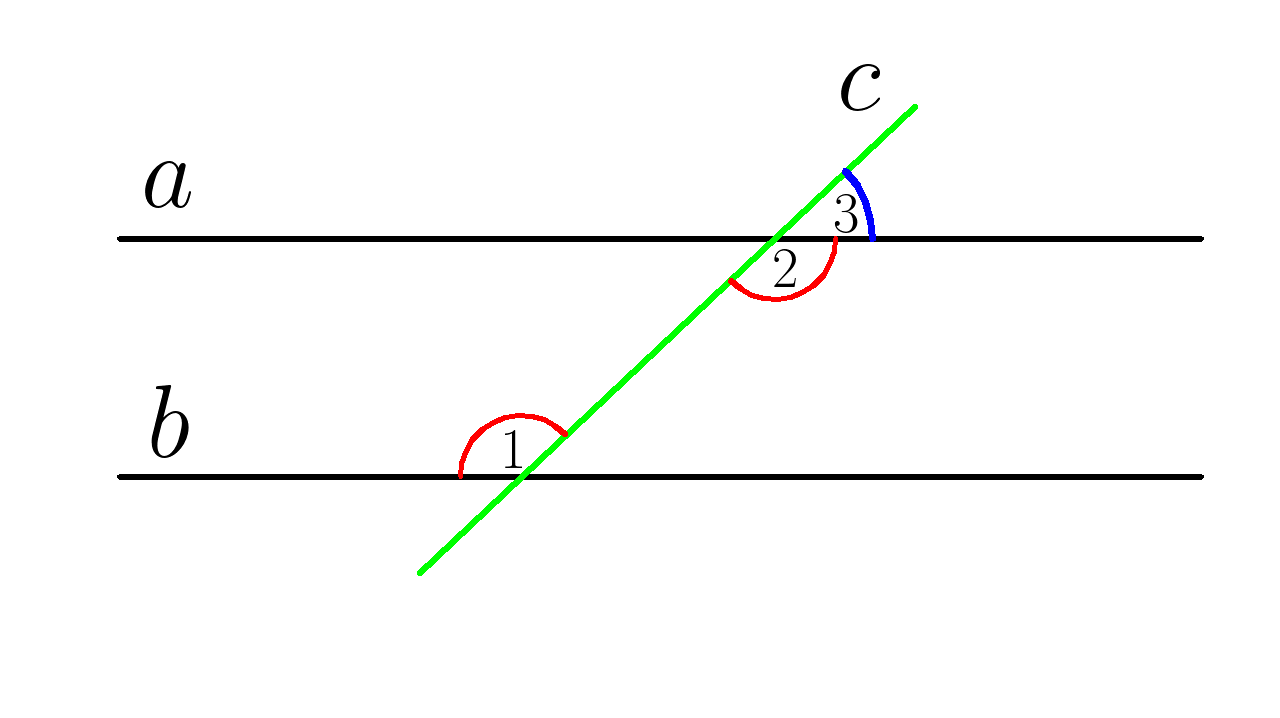
2. На рисунке \( a \; \left | \right | \; b , \) найти \(\angle 3, \; \)если \( \; \angle 1 = 120^0 \)
Показать ответ Показать решение Видеорешение

Ответ: \(60^0 \)

\( \angle 2= \angle 1 = 120^0 \) (так как они накрест лежащие при \( a \; \left | \right | \; b \) )
\( \angle 2 и \angle 3 \) смежные, поэтому:
\( \angle 2 + \angle 3 = 180^0 \)
\( 120^0 + \angle 3 = 180^0 \)
\( \angle 3 = 180^0- 120^0=60^0 \)
Ответ: \( \angle 3 = 60^0 \)

ПОЗЖЕ

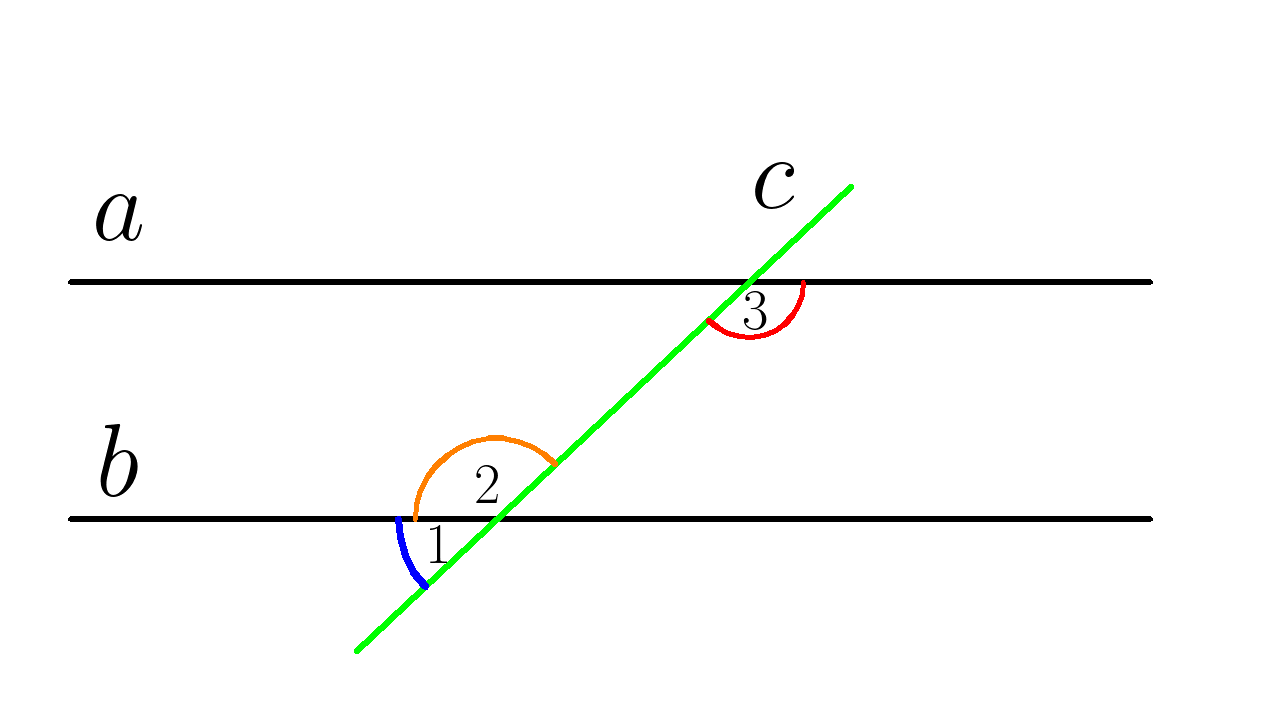
3. На рисунке \( a \; \left | \right | \; b , \) найти \(\angle 3, \; \)если \( \; \angle 1 = 30^0 \)
Показать ответ Показать решение Видеорешение

Ответ: \( \angle 3 = 150^0 \)

\( \angle 1 и \angle 2 \) смежные, поэтому:
\( \angle 1 + \angle 2 = 180^0 \)
\( 30^0 + \angle 2 = 180^0 \)
\( \angle 2 = 180^0- 30^0=150^0 \)
\( \angle 3= \angle 2 = 150^0 \) (так как они накрест лежащие при \( a \; \left | \right | \; b \) )
Ответ: \( \angle 3 = 150^0 \)

ПОЗЖЕ

4. На рисунке \( a \; \left | \right | \; b , \) доказать \(\angle 1= \angle 2 \)
Показать подсказку Показать решение Видеорешение

Доказательство от противного (от противоположного) :
Представим, что \(\angle 1 \neq \angle 2 \)

Дано: \( a \; \left | \right | \; b \ \ \ \ \ \ \ \ c- \) секущая

Доказать: \(\angle 1= \angle 2 \)
Доказательство от противного (от противоположного) :
Представим, что \(\angle 1 \neq \angle 2 \)
Проведем прямую \(d \) так, что \(\angle 1= \angle 3 \)
\(\Rightarrow\) \( b \; \left | \right | \; d \)

Получается, что через точку \( K \) проходят две различные прямые параллельные прямой \( a . \)
А это противоречит аксиоме:
Через точку K , не лежащую на прямой \( b \) можно провести прямую \(a\) , параллельную прямой \( b \), причем только одну. Значит \(\angle 1= \angle 2 \)

ПОЗЖЕ