Сумма углов треугольника

Сумма углов любого треугольника равна \(180^0 \)

  

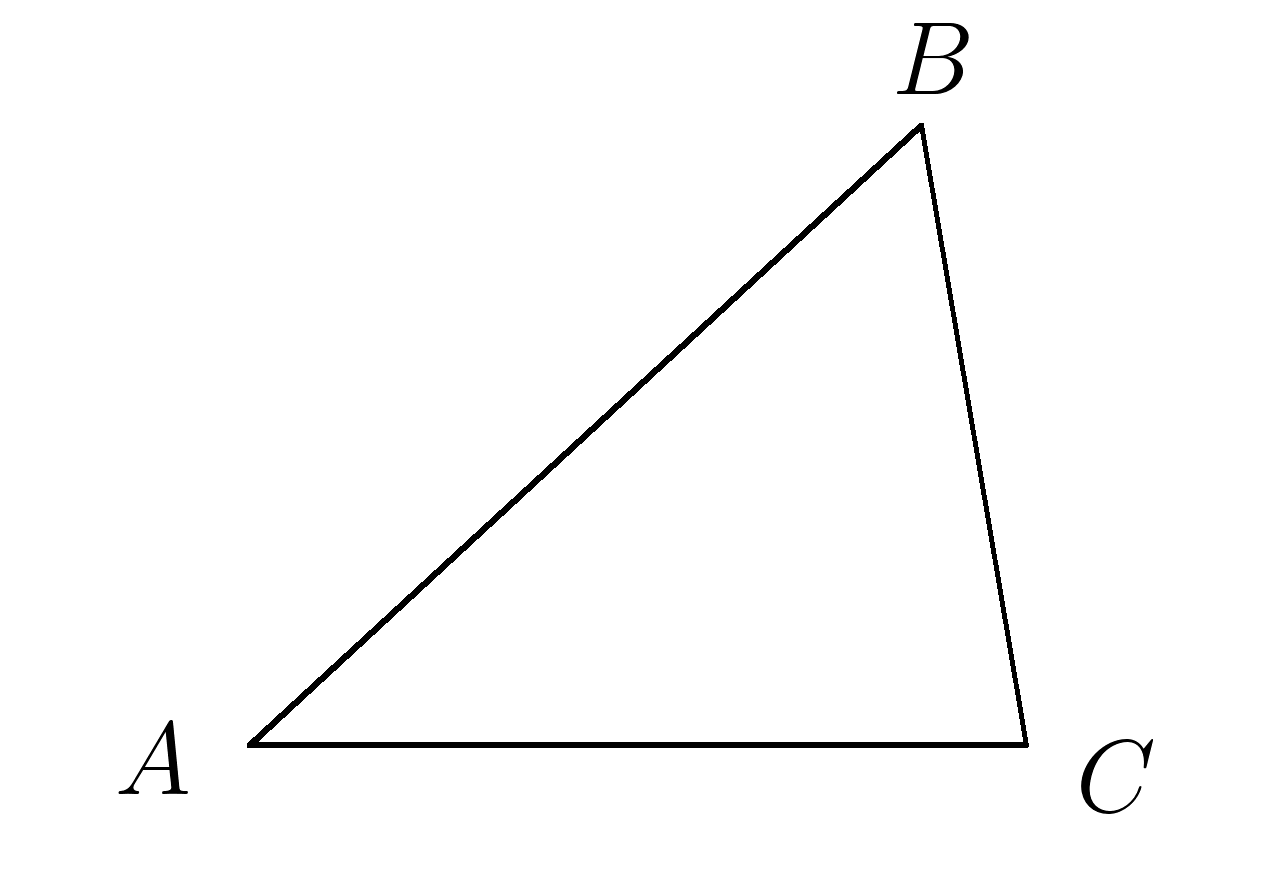
\( \angle A+\angle B+\angle C=180^0 \)

---

Доказательство:

Проведем прямую \( r \) параллельную стороне \(AB \)


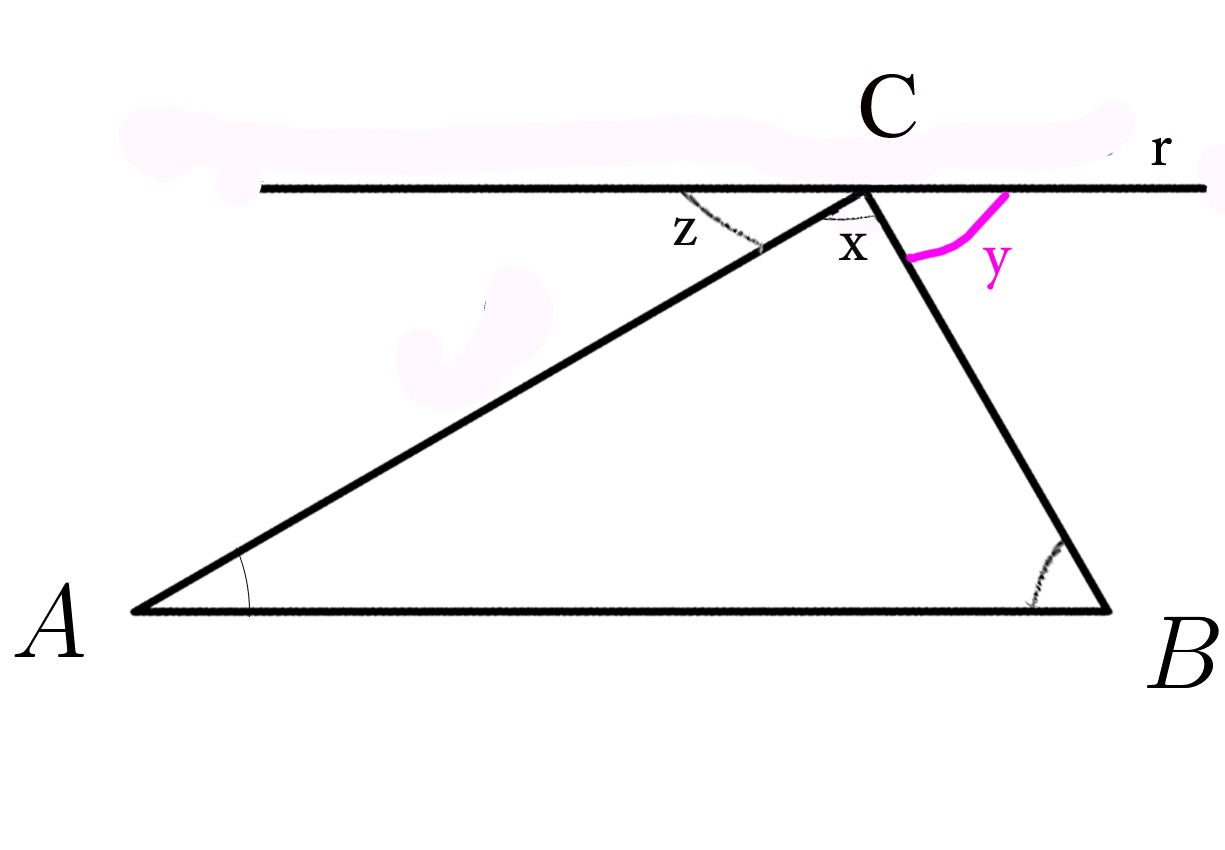
\( \angle z + \angle x + \angle y =180^0 \)

\( \angle z = \angle A \ \ \ \ \ \) (накрест лежащие при \( AB \; \left | \right | \; r \) и секущей AC )

\( \angle y = \angle B \ \ \ \ \ \) (накрест лежащие при \( AB \; \left | \right | \; r \) и секущей CB )

меняем в уравнении \( \angle z \) на \( \angle A \)

меняем в уравнении \( \angle y \) на \( \angle B \)

\( \angle A + \angle x+ \angle B=180^0 \)

\( \angle A + \angle C+ \angle B=180^0 \)

Теорема доказана

---

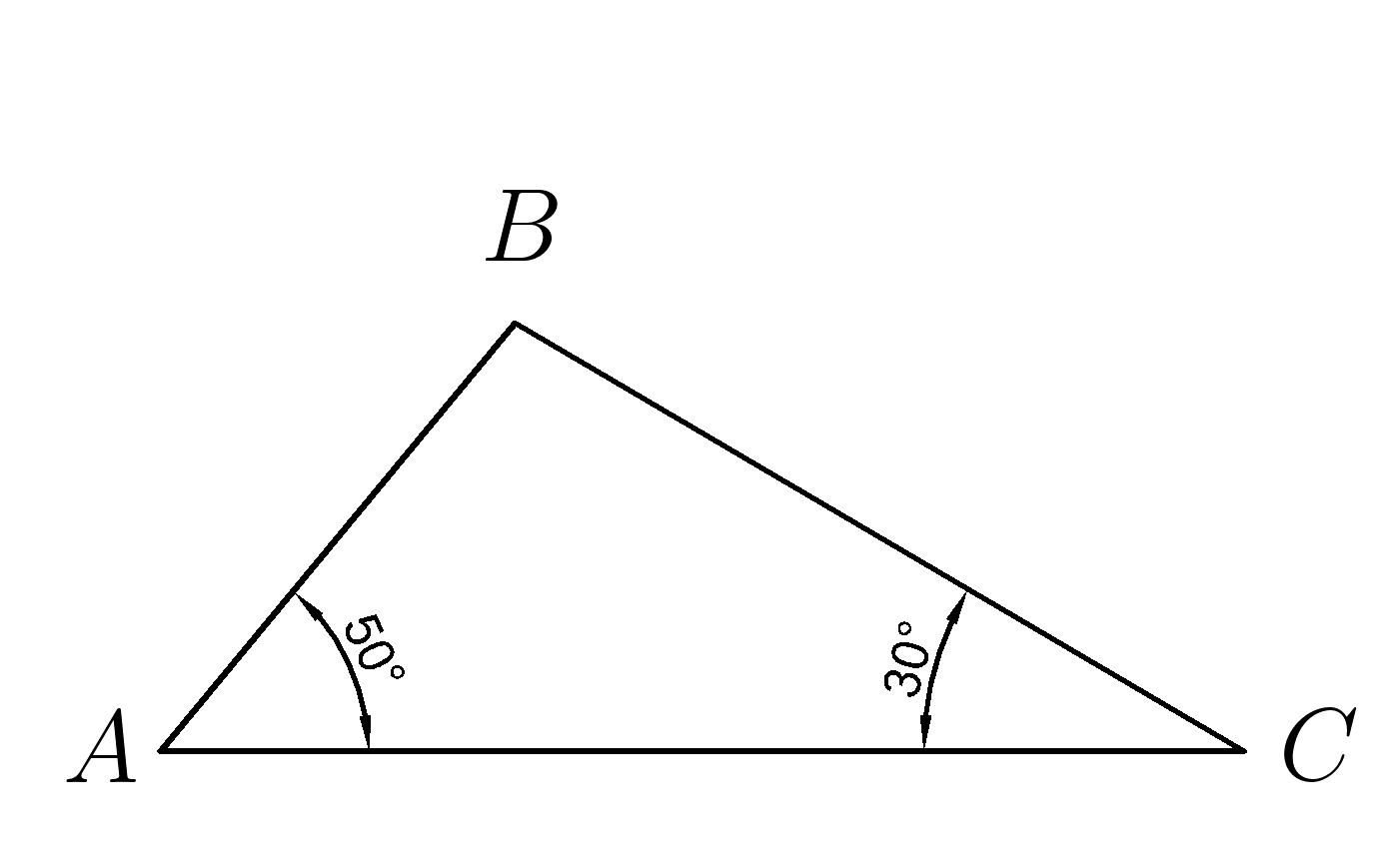
1.  По данным рисунка найти угол \( B \)
Показать ответ Показать решение Видеорешение

ПОЗЖЕ

---

---

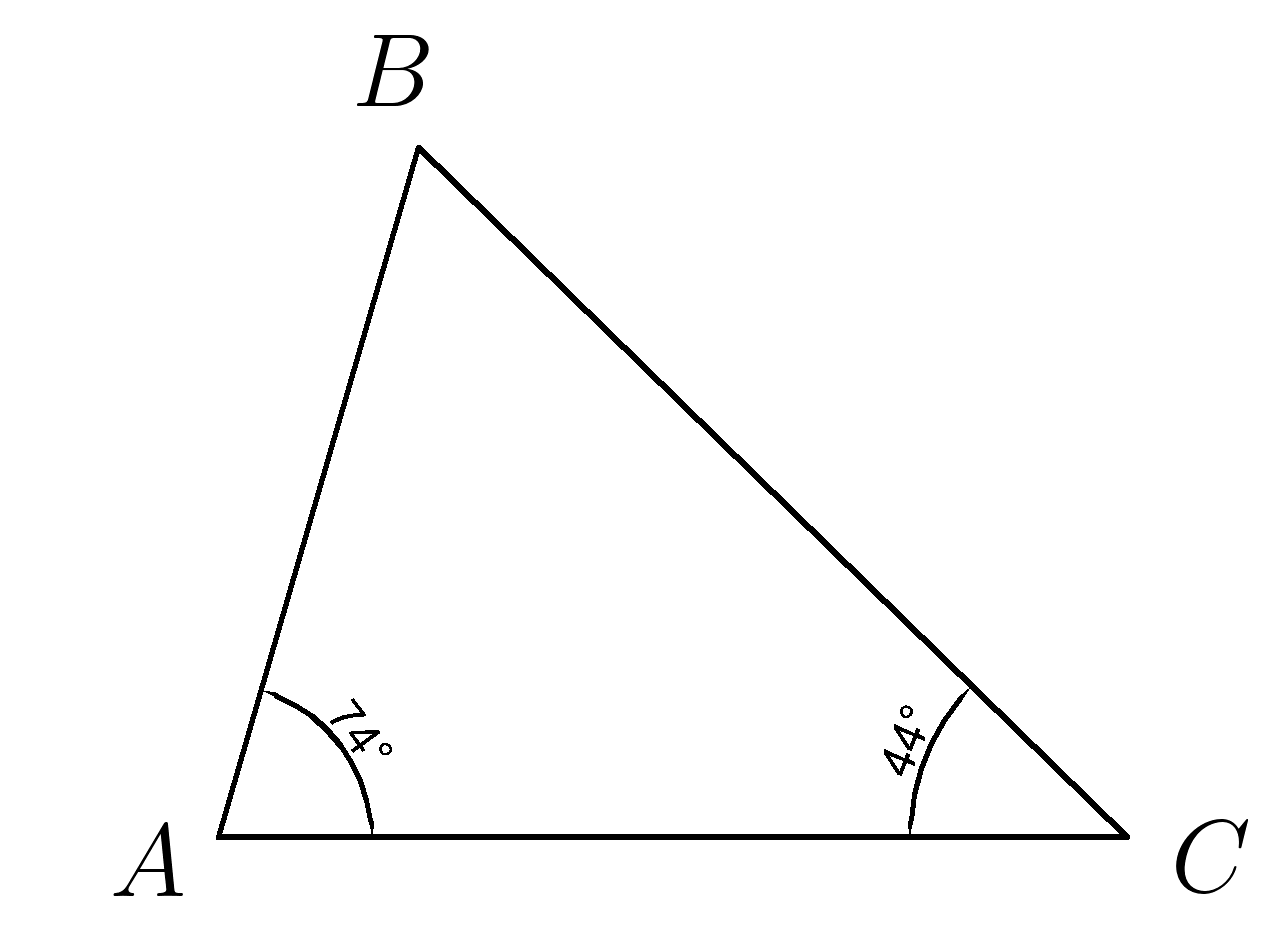
2.  По данным рисунка найти угол \( B \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle B=62^0\)

\( \angle A+\angle B+\angle C=180^0 \)

\( 74^0+\angle B+44^0=180^0 \)

\( 118^0+\angle B=180^0 \)

\( \angle B=180^0- 118^0 \)

\( \angle B=62^0\)

Ответ: \( \angle B=62^0\)

ПОЗЖЕ

---

---

3.  По данным рисунка найти угол \( B \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle B=90^0\)

\( \angle A+\angle B+\angle C=180^0 \)

\( 70^0+\angle B+20^0=180^0 \)

\( 90^0+\angle B=180^0 \)

\( \angle B=180^0- 90^0 \)

\( \angle B=90^0\)

Ответ: \( \angle B=90^0\)

ПОЗЖЕ

---

---

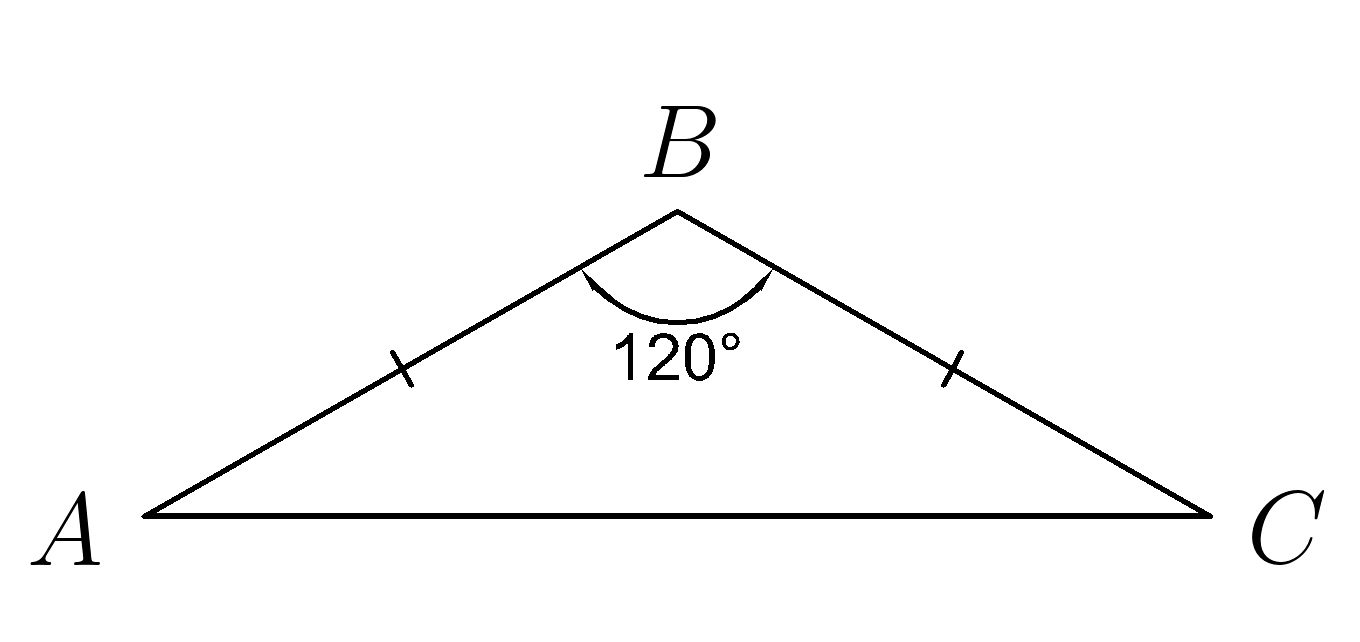
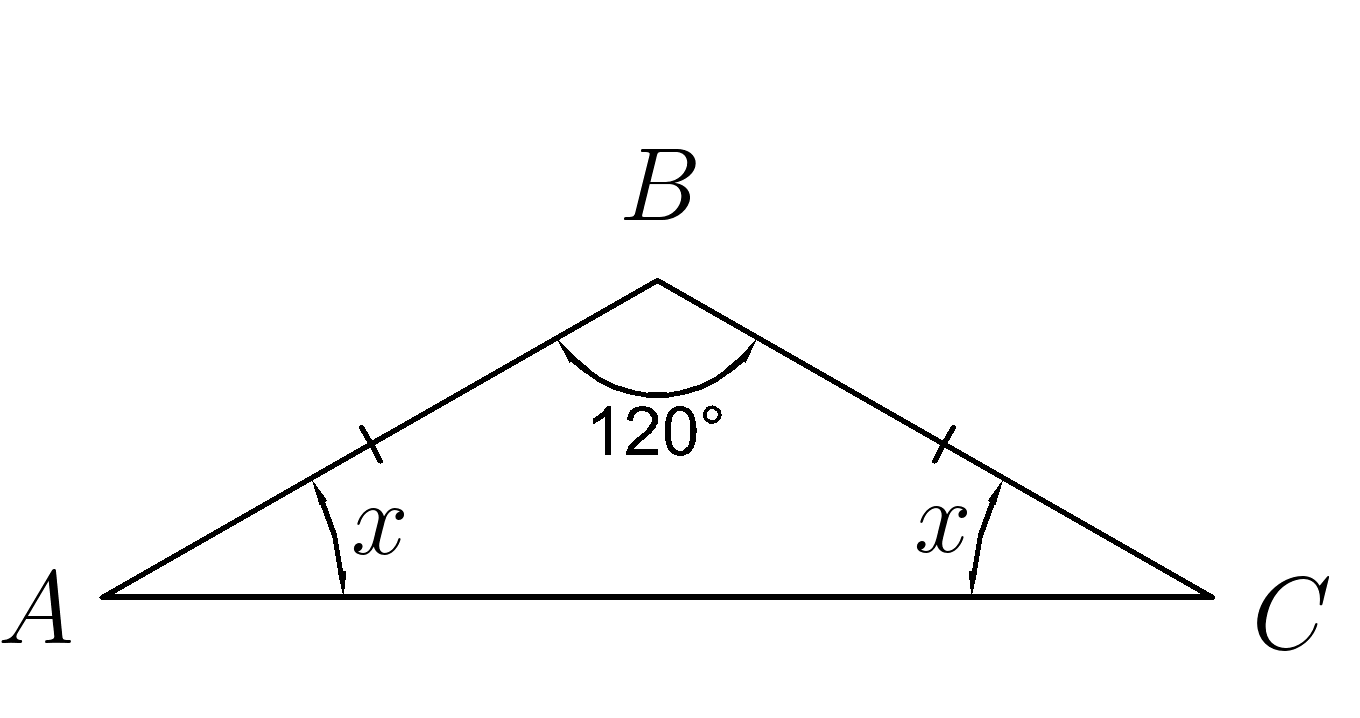
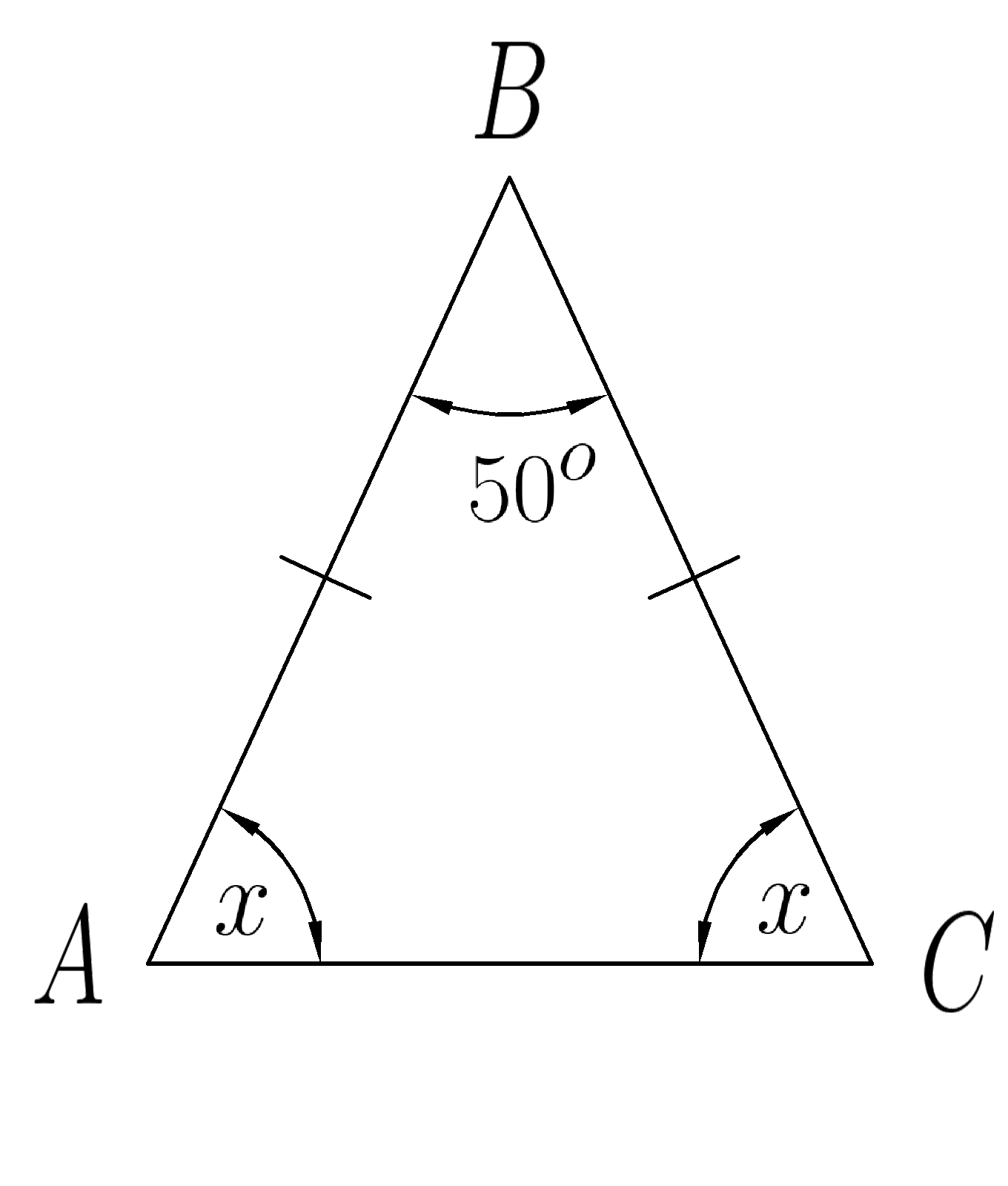
4.  Треугольник \(ABC \) равнобедренный. По данным рисунка найти углы \( A \; и \;C \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle A=30^0,\;\; \angle C=30^0\)

\( \angle A+\angle B+\angle C=180^0 \)

В равнобедренном треугольнике углы при основании равны \( \angle A= \angle C\)

Пусть \( \angle A=x \), тогда \( \angle C=x \)


\(x+x+120=180 \)

\(2x+120=180 \)

\(2x=180-120 \)

\(2x=60 \)

\(x=30 \)

\( \angle A= \angle C=30^0\)

Ответ: \( \angle A=30^0,\;\; \angle C=30^0\)

ПОЗЖЕ

---

---

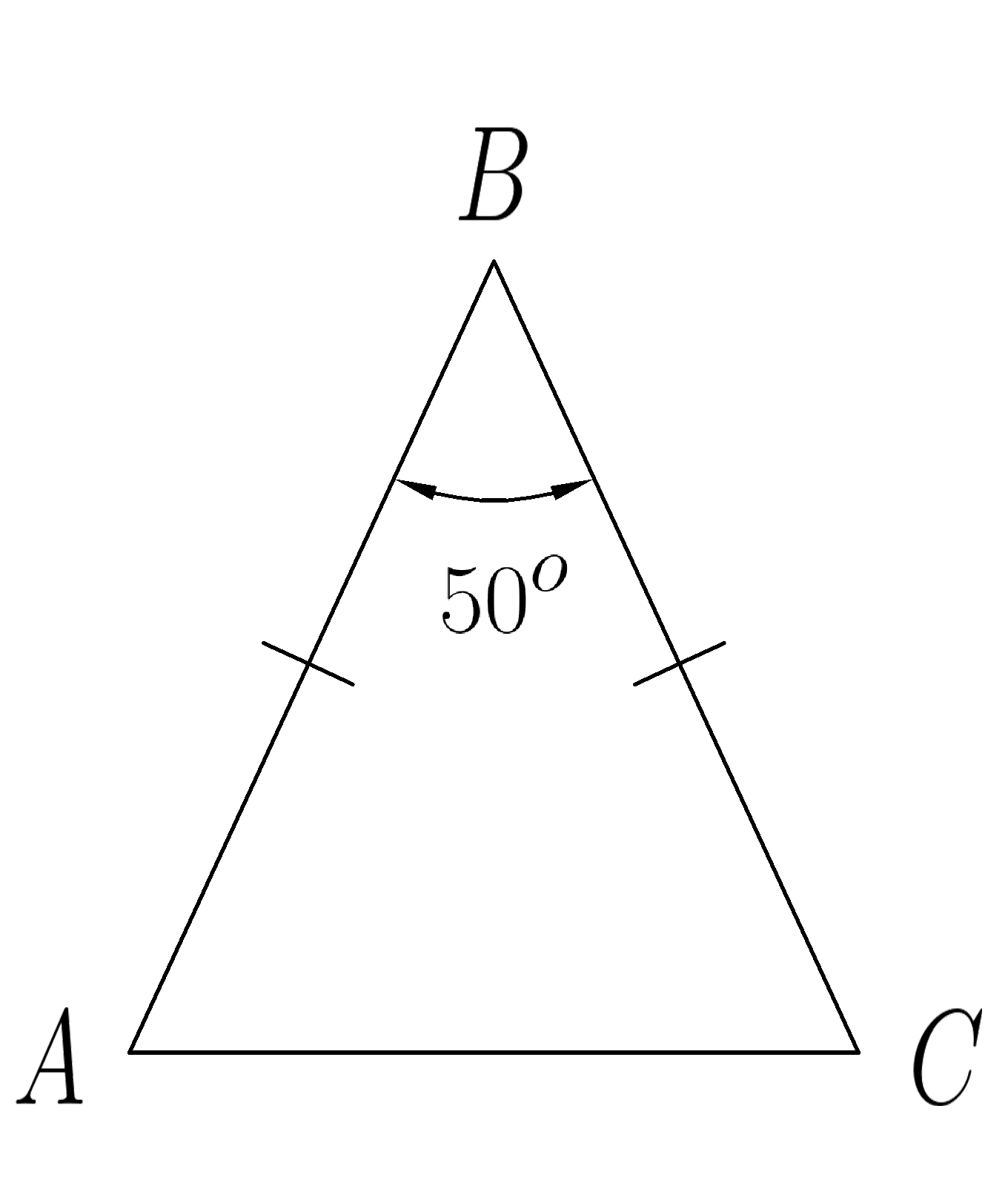
5.  Треугольник \(ABC \) равнобедренный. По данным рисунка найти углы \( A \; и \;C \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle A=65^0,\;\; \angle C=65^0\)

\( \angle A+\angle B+\angle C=180^0 \)

В равнобедренном треугольнике углы при основании равны \( \angle A= \angle C\)

Пусть \( \angle A=x \), тогда \( \angle C=x \)


\(x+x+50=180 \)

\(2x+50=180 \)

\(2x=180-50 \)

\(2x=130 \)

\(x=65 \)

\( \angle A= \angle C=65^0\)

Ответ: \( \angle A=65^0,\;\; \angle C=65^0\)

ПОЗЖЕ

---

---

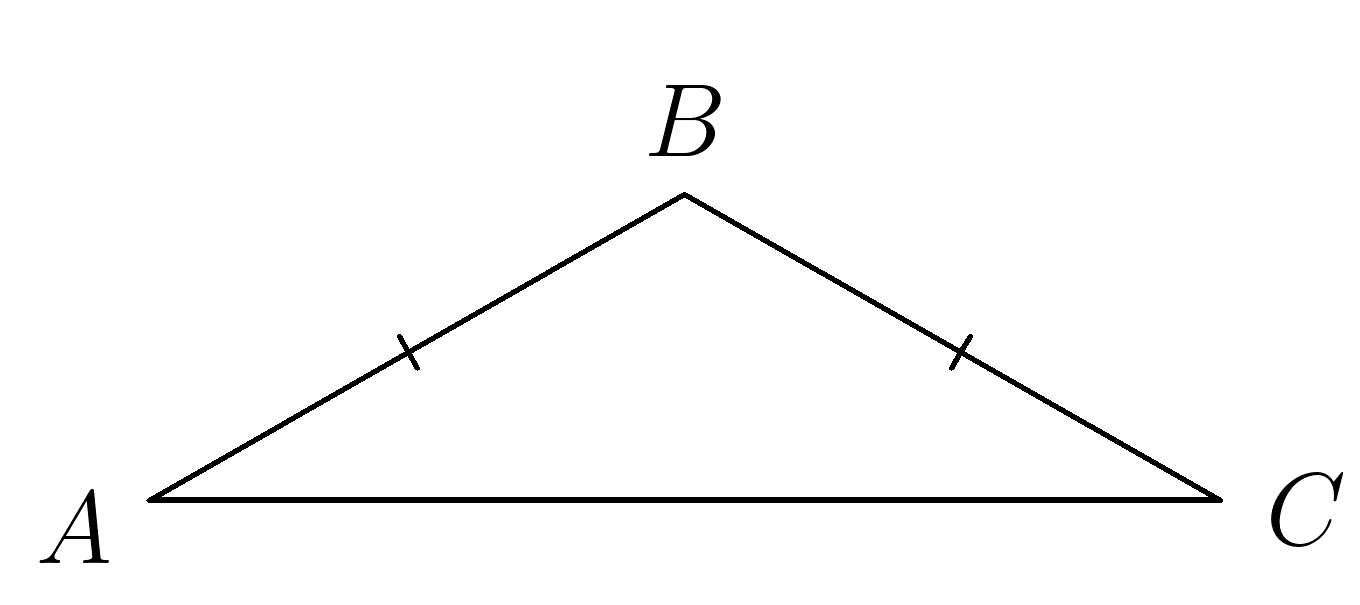
6.  Треугольник \(ABC \) равнобедренный \( \; AB=BC , \; \; \angle A=25^0 \). Найти угол \( B \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle B=130^0 \)

\( \angle A+\angle B+\angle C=180^0 \)

В равнобедренном треугольнике углы при основании равны \( \angle C=\angle A=25^0\)

\( 25^0+\angle B+25^0=180^0 \)

\( 50^0+\angle B=180^0 \)

\( \angle B=180^0- 50^0 \)

\( \angle B=130^0\)

Ответ: \( \angle B=130^0\)

ПОЗЖЕ

---

---

7.  Треугольник \(ABC \) равнобедренный \( \; AB=BC , \; \; \angle B=140^0 \). Найти угол \( A \)
Показать ответ Показать решение Видеорешение

  

Ответ: \( \angle A=20^0 \)

\( \angle A+\angle B+\angle C=180^0 \)

В равнобедренном треугольнике углы при основании равны \( \angle A= \angle C\)

Пусть \( \angle A=x \), тогда \( \angle C=x \)
\(x+x+140=180 \)

\(2x+140=180 \)

\(2x=180-140 \)

\(2x=40 \)

\(x=20 \)

\( \angle A= \angle C=20^0\)

Ответ: \( \angle A=20^0 \)

ПОЗЖЕ

---