Репетитор
по физике

916 478 1032




Репетитор
по алгебре

916 478 1032


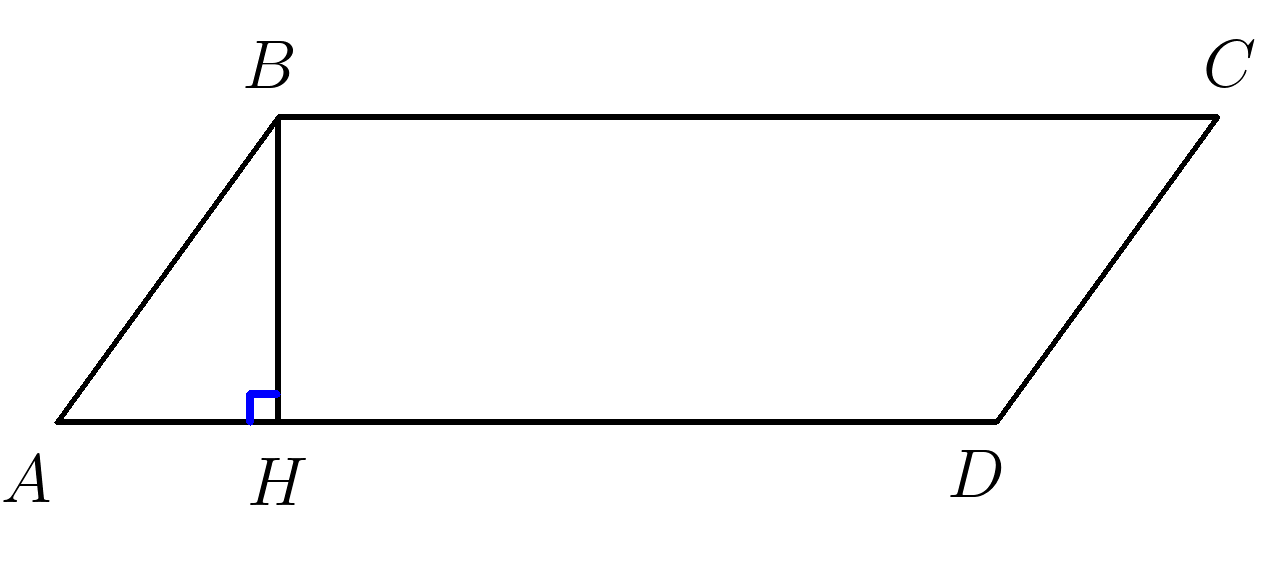
Параллелограмм .

Что мы должны знать о параллелограмме?

1. Параллелограмм это четырехугольник у которого противолежащие стороны параллельны и равны

2. Сумма углов любого четырехугольнка равна 360 градусов

3. Площадь параллелограмма равна произведению(умножению) его стороны на опущенную на нее высоту:
Площадь параллелограмма
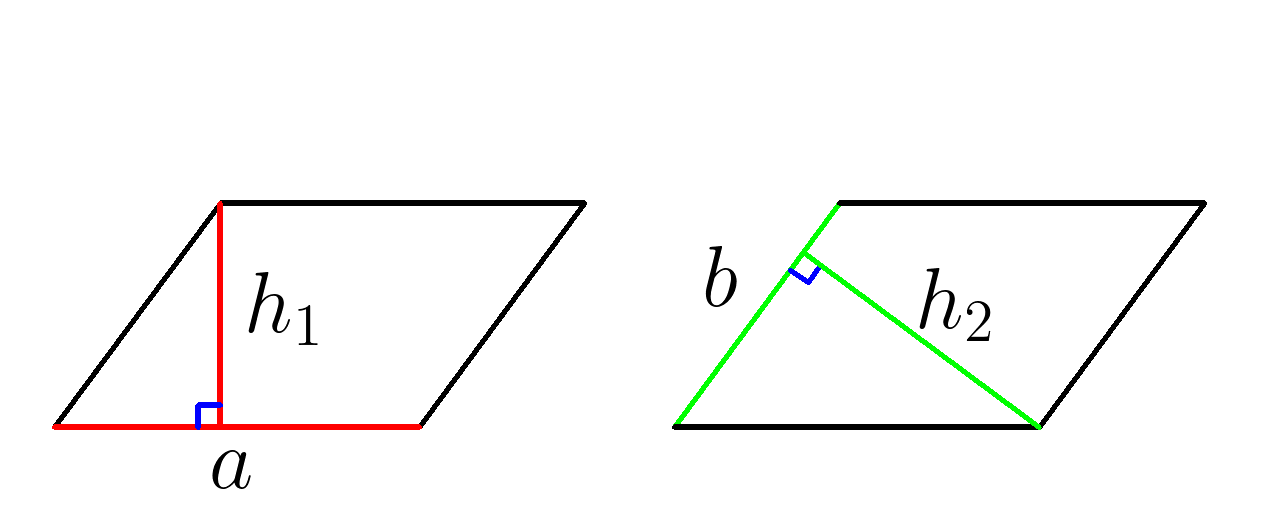
\(S=h_1 \cdot a \)     или    \( S=h_2 \cdot b \)



4. Сумма двух углов прилегающих к любой стороне параллелограмма равна \(180^0\)





параллелограмм

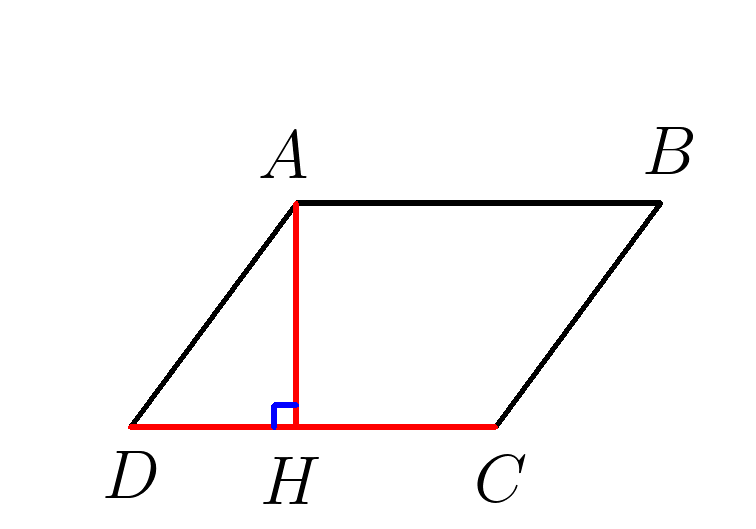
1.  В параллелограмме \(ABCD \) \( \;\; CD=5, \; AH=2 \). Найти площадь параллелограмма


  

Ответ: \(10 \)

Площадь параллелограмма равна произведению(умножению) его стороны на опущенную на нее высоту:
\( S=CD \cdot AH=5 \cdot 2 = 10 \)

Ответ: 10


ПОЗЖЕ


параллелограмм

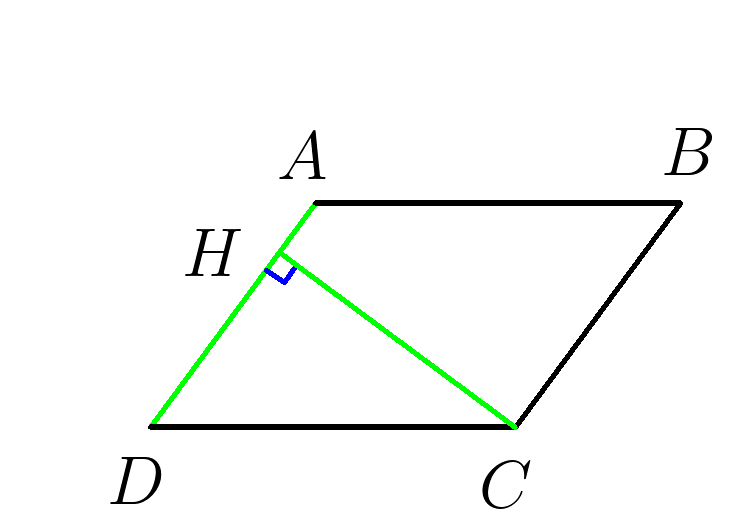
2.  В параллелограмме \(ABCD \) \( \;\; AD=14, \; CH=3 \). Найти площадь параллелограмма


  

Ответ: \(42 \)

Площадь параллелограмма равна произведению(умножению) его стороны на опущенную на нее высоту:
\( S=AD \cdot CH=14 \cdot 3 = 42 \)

Ответ: 42


ПОЗЖЕ

параллелограмм

3.  Площадь параллелограмма \(ABCD \) равна 64. Высота \(AH \) равна 4. Найти сторону \(DC\)


  

Ответ: \(16 \)

Площадь параллелограмма равна произведению(умножению) его стороны на опущенную на нее высоту:
\( S=CD \cdot AH \)

\( CD=\dfrac{S}{ AH}=\dfrac{64}{4}=16 \)

Ответ: 16


ПОЗЖЕ

параллелограмм

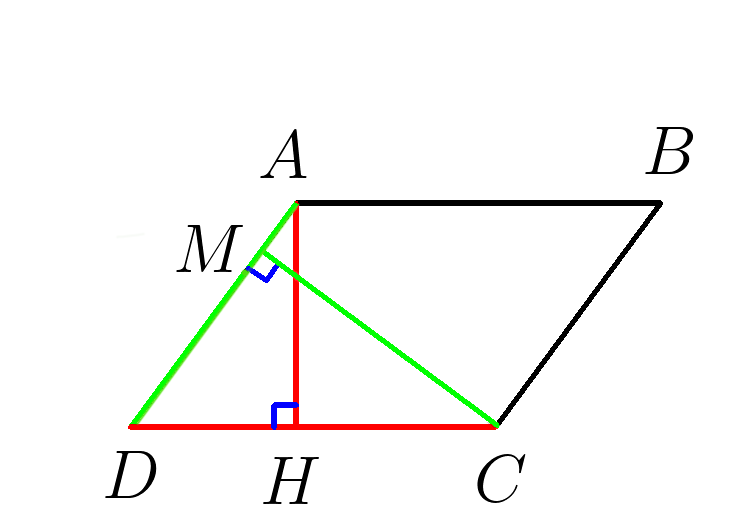
4.  В параллелограмме \(ABCD \) высота \(AH=15 , \; CD=10, \;\;AD=50. \) Найти высоту \( CM \)


  

Ответ: \( CM=3 \)

\( S=AH \cdot CD \)
\( S=AD \cdot CM \)

\(AH \cdot CD= AD \cdot CM \)

\(15 \cdot 10= 50 \cdot CM \)

\( CM=\dfrac{150}{50}=3 \)

Ответ: \( CM=3 \)


ПОЗЖЕ


5.  Площадь параллелограмма равна 100 , а его стороны равны 25 и 10, найти меньшую высоту этого параллелограмма


  

Ответ: \( h_1=4 \)


Площадь параллелограмма

\( S=h_1\cdot a \)
\( 100=h_1\cdot 25 \)
\( h_1=4 \)

\( S=h_2\cdot b \)
\( 100=h_2\cdot 10 \)
\( h_2=10 \)

Ответ: \( h_1=4 \)


ПОЗЖЕ

параллелограмм

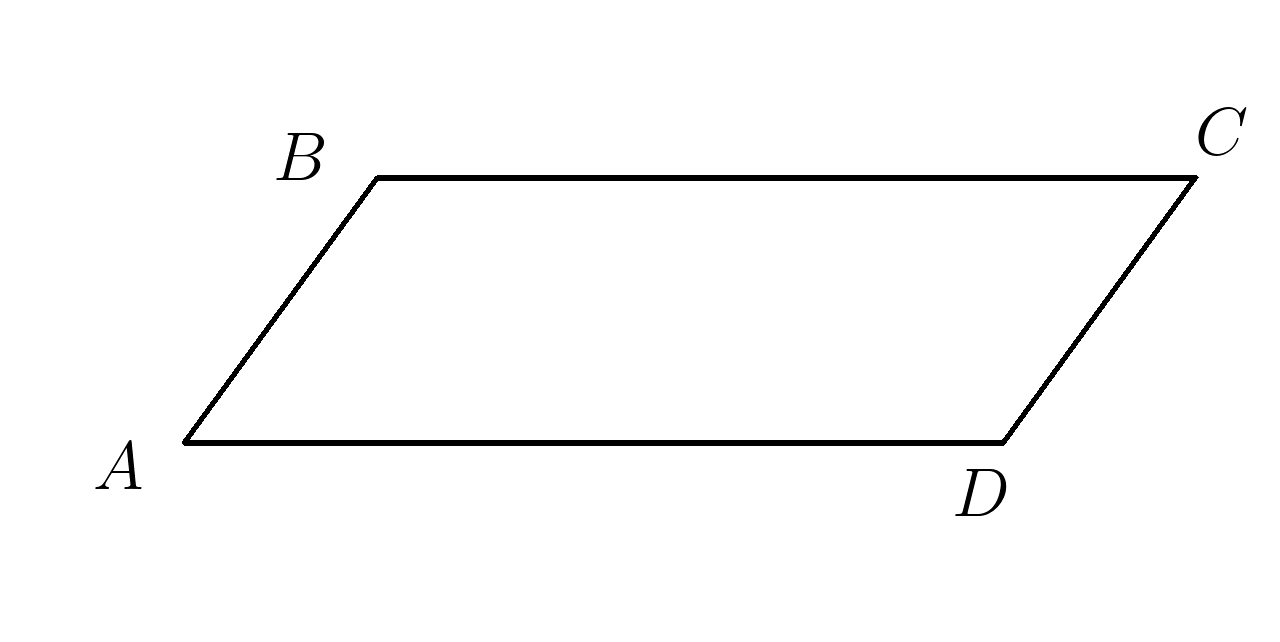
6.  Синус угла \(A \) равен \(0,25,\;\; AB=4, \;\;AD=11 \). Найти площадь этого параллелограмма


  

Ответ: \( 11 \)


Проведем высоту \(BH : \)
Площадь параллелограмма
\( sin \;\; ∡BAH=0,25 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;sin \;\; ∡BAH=\dfrac{BH}{AB} \)

\( 0,25=\dfrac{BH}{AB} \)

\( 0,25=\dfrac{BH}{4} \)

\( BH=4 \cdot 0,25=1 \)

\(S= BH \cdot AD= 1 \cdot 11 =11 \)

Ответ: \( S=11 \)


ПОЗЖЕ

параллелограмм

7.  Угол \(A \) равен \(45^0,\;\; AB=2\sqrt{2}, \;\;AD=11 \). Найти площадь этого параллелограмма


  

Ответ: \( 22 \)


Проведем высоту \(BH : \)
Площадь параллелограмма
\( sin \;\; ∡BAH=\dfrac{\sqrt{2}}{2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;sin \;\; ∡BAH=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{2}}{2}=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{2}}{2}=\dfrac{BH}{2\sqrt{2}} \)

\( BH=2\sqrt{2} \cdot \dfrac{\sqrt{2}}{2}=2 \)

\(S= BH \cdot AD= 2 \cdot 11 =22 \)

Ответ: \( S=22 \)


ПОЗЖЕ

параллелограмм

8.  Угол \(B \) равен \(135^0,\;\; AB=2\sqrt{2}, \;\;AD=11 \). Найти площадь этого параллелограмма


  

Ответ: \( 22 \)

\( ∡A+∡B=180^0 \)

\( ∡A+135^0= 180^0 \)

\( ∡A=45^0 \)

Проведем высоту \(BH : \)
Площадь параллелограмма
\( sin \;\; ∡BAH=\dfrac{\sqrt{2}}{2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;sin \;\; ∡BAH=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{2}}{2}=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{2}}{2}=\dfrac{BH}{2\sqrt{2}} \)

\( BH=2\sqrt{2} \cdot \dfrac{\sqrt{2}}{2}=2 \)

\(S= BH \cdot AD= 2 \cdot 11 =22 \)

Ответ: \( S=22 \)


ПОЗЖЕ

параллелограмм

9.  Угол \(D \) равен \(120^0,\;\; AB=10\sqrt{3}, \;\;AD=34 \). Найти площадь этого параллелограмма


  

Ответ: \( 510 \)

\( ∡A+∡D=180^0 \)

\( ∡A+120^0= 180^0 \)

\( ∡A=60^0 \)

Проведем высоту \(BH : \)
Площадь параллелограмма
\( sin \;\; ∡BAH=\dfrac{\sqrt{3}}{2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;sin \;\; ∡BAH=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{3}}{2}=\dfrac{BH}{AB} \)

\( \dfrac{\sqrt{3}}{2}=\dfrac{BH}{10\sqrt{3}} \)

\( BH=10\sqrt{3} \cdot \dfrac{\sqrt{3}}{2}=15 \)

\(S= BH \cdot AD= 15 \cdot 34 =510 \)

Ответ: \( S=510 \)


ПОЗЖЕ

параллелограмм

10.  Площадь этого параллелограмма равна \(100, \;\; AD=20, \;\; AB=8 \;\; \).Найти синус острого угла этого параллелограмма.


  

Ответ: \( 0,625 \)

Проведем высоту \(BH \) и вычислим ее:
Площадь параллелограмма
\(BH=\dfrac{S}{AD}=\dfrac{100}{20}=5 \)

\( sin \;\; ∡BAH=\dfrac{BH}{AB}=\dfrac{5}{8}=0,625 \)

Ответ: \( sin \;\; ∡A=0,625\)


ПОЗЖЕ