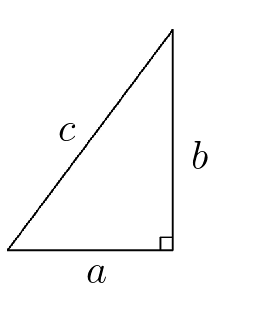
\(c^2 = a^2 + b^2 \)
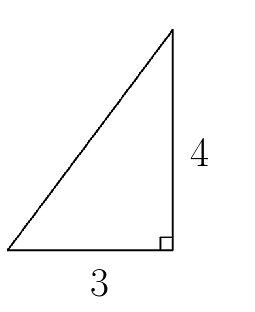
1. Один из катетов прямоугольного треугольника равен 3 см, а другой катет равен 4 см.Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=3 \; \; \;\; \;\; \; \; b=4 \)
\(c^2 = \; 3^2 \; + \; 4^2 \)
\(c^2 = 9+16 \)
\(c^2 = 25 \)
\( c=\sqrt{25} \)
\(c=5\)
Ответ: \(c=5\)
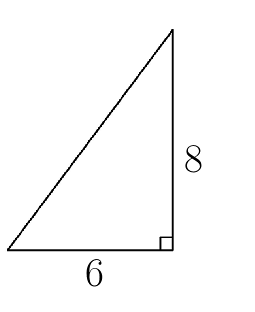
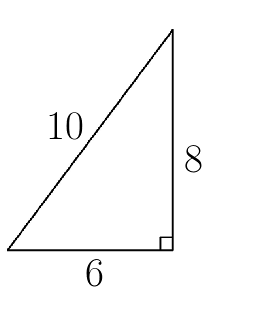
2. Один из катетов прямоугольного треугольника равен 6 см, а другой катет равен 8 см.Найти гипотенузу.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=6 \; \; \;\; \;\; \; \; b=8 \)
\(c^2 = \; 6^2 \; + \; 8^2 \)
\(c^2 = 36+64 \)
\(c^2 = 100 \)
\( c=\sqrt{10} \)
\(c=10\)
Ответ: \(c=10\)
3. Один из катетов прямоугольного треугольника равен 5 см, а другой катет равен 12 см.Найти гипотенузу.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=5 \; \; \;\; \;\; \; \; b=12 \)
\(c^2 = \; 5^2 \; + \; 12^2 \)
\(c^2 = 25+144 \)
\(c^2 = 169 \)
\( c=\sqrt{169} \)
\(c=13\)
Ответ: \(c=13\)

4. Один из катетов прямоугольного треугольника равен 9 см, а другой катет равен 12 см.Найти гипотенузу.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=9 \; \; \;\; \;\; \; \; b=12 \)
\(c^2 = \; 9^2 \; + \; 12^2 \)
\(c^2 = 81+144 \)
\(c^2 = 225 \)
\( c=\sqrt{225} \)
\(c=15\)
Ответ: \(c=15\)


5. Один из катетов прямоугольного треугольника равен 15 см, а другой катет равен 8 см.Найти гипотенузу.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=15 \; \; \;\; \;\; \; \; b=8 \)
\(c^2 = \; 15^2 \; + \; 8^2 \)
\(c^2 = 225+64 \)
\(c^2 = 225 \)
\( c=\sqrt{289} \)
\(c=17\)
Ответ: \(c=17\)


6. Один из катетов прямоугольного треугольника равен 3 см, а гипотенуза равна 5 см, найти другой катет.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=3 \; \; \;\; \;\; \; \; c = 5 \)
\(5^2 = \; 3^2 \; + \; b^2 \)
\(25 = 9+b^2 \)
\(25-9 = b^2 \)
\(16 = b^2 \)
\( b^2 = 16 \)
\( b=\sqrt{16} \)
\(b=4\)
Ответ: \(b=4\)


7. Один из катетов прямоугольного треугольника равен 6 см, а гипотенуза равна 10 см, найти другой катет.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=6 \; \; \;\; \;\; \; \; c = 10 \)
\(10^2 = \; 6^2 \; + \; b^2 \)
\(100 = 36+b^2 \)
\(100-36 = b^2 \)
\(64 = b^2 \)
\( b^2 = 64 \)
\( b=\sqrt{64} \) или \( b=-\sqrt{64} \)
\(b=8\) или \( b=-8 \)
Длина не может быть отрицательной, поэтому \(b=8\)
Ответ: \(b=8\)


8. Один из катетов прямоугольного треугольника равен 15 см, а гипотенуза равна 17 см, найти другой катет.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=15 \; \; \;\; \;\; \; \; c = 17 \)
\(17^2 = \; 15^2 \; + \; b^2 \)
\(289 = 225+b^2 \)
\(289-225 = b^2 \)
\(64 = b^2 \)
\( b^2 = 64 \)
\( b=\sqrt{64} \) или \( b=-\sqrt{64} \)
\(b=8\) или \( b=-8 \)
Длина не может быть отрицательной, поэтому \(b=8\)
Ответ: \(b=8\)


9. Один из катетов прямоугольного треугольника равен 9 см, а гипотенуза равна 15 см, найти другой катет.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=9 \; \; \;\; \;\; \; \; c = 15 \)
\(15^2 = \; 9^2 \; + \; b^2 \)
\(225 = 81+b^2 \)
\(225-81 = b^2 \)
\(144 = b^2 \)
\( b^2 = 144 \)
\( b=\sqrt{144} \) или \( b=-\sqrt{144} \)
\(b=12\) или \( b=-12 \)
Длина не может быть отрицательной, поэтому \(b=12\)
Ответ: \(b=12\)


10. Один из катетов прямоугольного треугольника равен 40 см, а гипотенуза равна 50 см, найти другой катет.
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=40 \; \; \;\; \;\; \; \; c = 50 \)
\(50^2 = \; 40^2 \; + \; b^2 \)
\(2500 = 1600+b^2 \)
\(2500-1600 = b^2 \)
\(900 = b^2 \)
\( b^2 = 900 \)
\( b=\sqrt{900} \) или \( b=-\sqrt{900} \)
\(b=30\) или \( b=-30 \)
Длина не может быть отрицательной, поэтому \(b=30\)
Ответ: \(b=30\)


11. Один из катетов прямоугольного треугольника равен \(\dfrac{3}{7} \) , а другой \(\dfrac{4}{7} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{3}{7} \) \(b =\) \(\dfrac{4}{7} \)
\(c^2 = \; (\dfrac{3}{7})^2 \; + \; (\dfrac{4}{7})^2 \)
\(c^2 = \dfrac{3^2}{7^2}+\dfrac{4^2}{7^2} \)
\(c^2 = \dfrac{9}{49}+\dfrac{16}{49} \)
\(c^2 = \dfrac{25}{49} \)
\( c = \sqrt{\dfrac{25}{49}} \) или \( c = -\sqrt{\dfrac{25}{49}} \)
\(c = \dfrac{5}{7}\) или \( c = -\dfrac{5}{7} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{5}{7}\)
Ответ: \(c = \dfrac{5}{7}\)


12. Один из катетов прямоугольного треугольника равен \(\dfrac{6}{11} \) , а другой \(\dfrac{8}{11} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{6}{11} \) \(b =\) \(\dfrac{8}{11} \)
\(c^2 = \; (\dfrac{6}{11})^2 \; + \; (\dfrac{8}{11})^2 \)
\(c^2 = \dfrac{6^2}{11^2}+\dfrac{8^2}{11^2} \)
\(c^2 = \dfrac{36}{121}+\dfrac{64}{121} \)
\(c^2 = \dfrac{100}{121} \)
\( c = \sqrt{\dfrac{100}{121}} \) или \( c = -\sqrt{\dfrac{100}{121}} \)
\(c = \dfrac{10}{11}\) или \( c = -\dfrac{10}{11} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{10}{11}\)
Ответ: \(c = \dfrac{10}{11}\)


13. Один из катетов прямоугольного треугольника равен \(\dfrac{5}{13} \) , а другой \(\dfrac{12}{13} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{5}{13} \) \(b =\) \(\dfrac{12}{13} \)
\(c^2 = \; (\dfrac{5}{13})^2 \; + \; (\dfrac{12}{13})^2 \)
\(c^2 = \dfrac{5^2}{13^2}+\dfrac{12^2}{13^2} \)
\(c^2 = \dfrac{25}{169}+\dfrac{144}{169} \)
\(c^2 = \dfrac{169}{169} \)
\(c^2 = 1 \)
\( c = 1 \) или \( c = -1 \)
Длина не может быть отрицательной, поэтому \(c = 1 \)
Ответ: \(c = 1\)


14. Один из катетов прямоугольного треугольника равен \(\dfrac{15}{19} \) , а другой \(\dfrac{8}{19} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
м
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{15}{19} \) \(b =\) \(\dfrac{8}{19} \)
\(c^2 = \; (\dfrac{15}{19})^2 \; + \; (\dfrac{8}{19})^2 \)
\(c^2 = \dfrac{15^2}{19^2}+\dfrac{8^2}{19^2} \)
\(c^2 = \dfrac{225}{361}+\dfrac{64}{361} \)
\(c^2 = \dfrac{289}{361} \)
\( c = \sqrt{\dfrac{289}{361}} \) или \( c = -\sqrt{\dfrac{289}{361}} \)
\(c = \dfrac{17}{19}\) или \( c = -\dfrac{17}{19} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{17}{19}\)
Ответ: \(c = \dfrac{17}{19}\)


15. Один из катетов прямоугольного треугольника равен \(\dfrac{1}{2} \) , а другой \(\dfrac{2}{3} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этого треугольника:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{1}{2} \) \(b =\) \(\dfrac{2}{3} \)
\(c^2 = \; (\dfrac{1}{2})^2 \; + \; (\dfrac{2}{3})^2 \)
\(c^2 = \dfrac{1^2}{2^2}+\dfrac{2^2}{3^2} \)
\(c^2 = \dfrac{1}{4}+\dfrac{4}{9} \)
\(c^2 = \dfrac{9}{36}+\dfrac{16}{36} \)
\(c^2 = \dfrac{25}{36} \)
\( c = \sqrt{\dfrac{25}{36}} \) или \( c = -\sqrt{\dfrac{25}{36}} \)
\(c = \dfrac{5}{6}\) или \( c = -\dfrac{5}{6} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{5}{6}\)
Ответ: \(c = \dfrac{5}{6}\)


16. Один из катетов прямоугольного треугольника равен \(\dfrac{3}{5} \) , а другой \(\dfrac{4}{5} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этой задачи:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{3}{5} \) \(b =\) \(\dfrac{4}{5} \)
\(c^2 = \; (\dfrac{3}{5})^2 \; + \; (\dfrac{4}{5})^2 \)
\(c^2 = \dfrac{3^2}{5^2}+\dfrac{4^2}{5^2} \)
\(c^2 = \dfrac{9}{25}+\dfrac{16}{25} \)
\(c^2 = \dfrac{25}{25} \)
\(c^2 = 1 \)
\( c = 1 \) или \( c = -1 \)
Длина не может быть отрицательной, поэтому \(c = 1 \)
Ответ: \(c = 1\)


17. Один из катетов прямоугольного треугольника равен \(1\dfrac{1}{2} \) , а другой \(\dfrac{4}{5} \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этой задачи:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{3}{2} \) \(b =\) \(\dfrac{4}{5} \)
\(c^2 = \; (\dfrac{3}{2})^2 \; + \; (\dfrac{4}{5})^2 \)
\(c^2 = \dfrac{3^2}{2^2}+\dfrac{4^2}{5^2} \)
\(c^2 = \dfrac{9}{4}+\dfrac{16}{25} \)
\( (25 \) \( (4 \)
\(c^2 = \dfrac{9}{4}+\dfrac{16}{25} \)
\(c^2 = \dfrac{9\cdot25}{100}+\dfrac{16\cdot4}{100} \)
\(c^2 = \dfrac{225}{100}+\dfrac{64}{100} \)
\(c^2 = \dfrac{289}{100} \)
\( c = \sqrt{\dfrac{289}{100}} \) или \( c = -\sqrt{\dfrac{289}{100}} \)
\(c = \dfrac{17}{10}\) или \( c = -\dfrac{17}{10} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{17}{10}=1,7\)
Ответ: \(c = 1,7\)


18. Один из катетов прямоугольного треугольника равен \(1\dfrac{3}{5} \) , а другой \( 3 \) .Найти гипотенузу
Показать ответ
Показать решение
Видеорешение
Запишем формулу теоремы Пифагора для этой задачи:
\( c^2 = a^2 + b^2 \)
\(a=\) \(\dfrac{8}{5} \) \(b =\) \(3 \)
\(c^2 = \; (\dfrac{8}{5})^2 \; + \; 3^2 \)
\(c^2 = \dfrac{8^2}{5^2}+9 \)
\(c^2 = \dfrac{64}{25}+9 \)
\(c^2 = 9\dfrac{64}{25} \)
\(c^2 = \dfrac{289}{25} \)
\( c = \sqrt{\dfrac{289}{25}} \) или \( c = -\sqrt{\dfrac{289}{25}} \)
\(c = \dfrac{17}{5}\) или \( c = -\dfrac{17}{5} \)
Длина не может быть отрицательной, поэтому \(c = \dfrac{17}{5}=3,4\)
Ответ: \(c = 3,4\)

| 


















