Угол между векторами.

Косинус угла между векторами \( \vec{a}(x_1;y_1) \ и \ \vec{b}(x_2;y_2) \) находится по формуле:

\( cos \ \alpha = \dfrac{x_1 \cdot x_2+y_1\cdot y_2 } { \sqrt {x_{1}^2+y_{1}^2}\cdot \sqrt {x_{2}^2+y_{2}^2} } \)

\( (x_1;y_1) \) это координаты вектора \( \vec{a} \)
\( (x_2;y_2) \) это координаты вектора \( \vec{b} \)

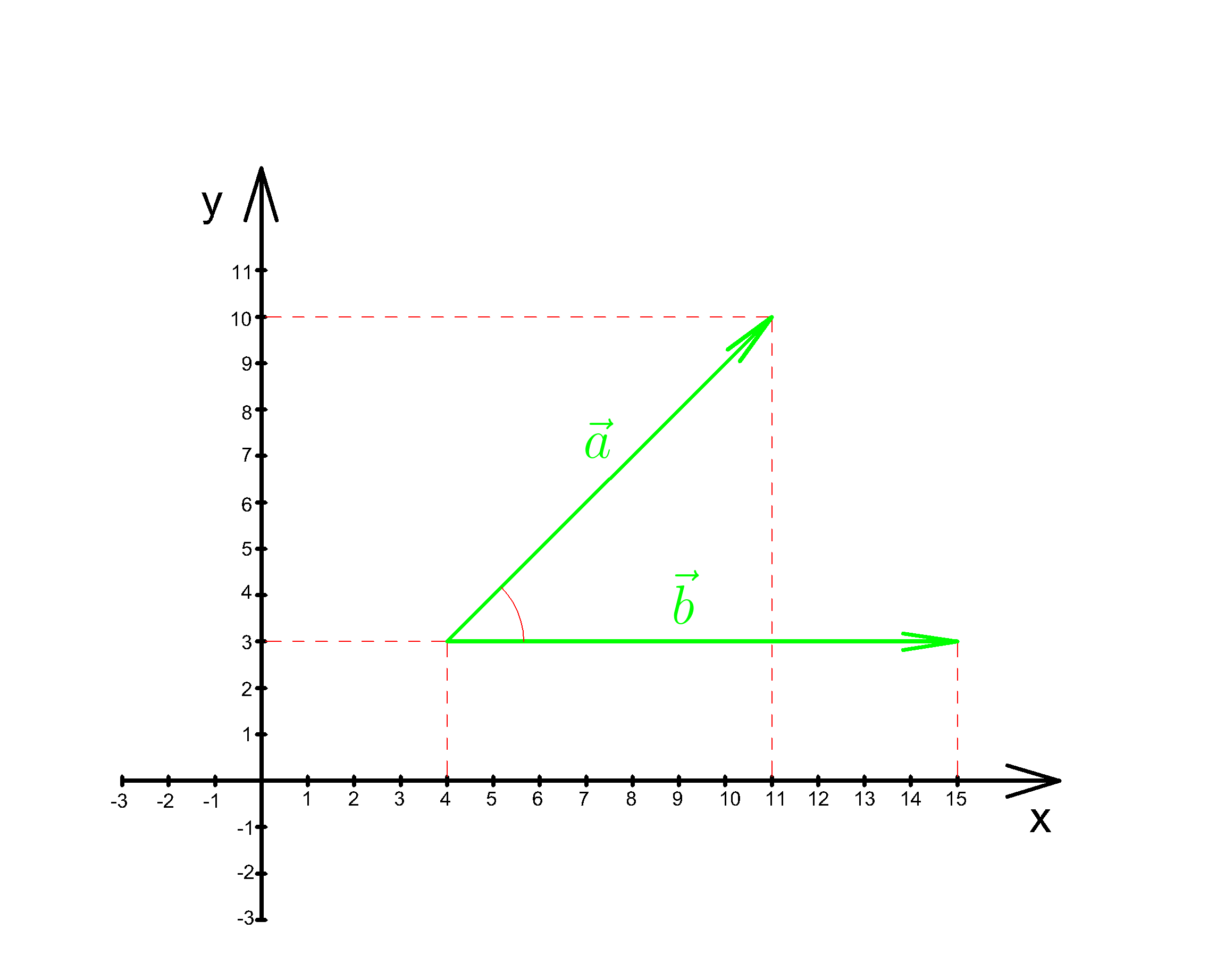
1. Найти угол между векторами \(\vec{a} \) и \(\vec{b} \)
Показать ответ Показать решение Видеорешение

Ответ: \( 45^0 \)

Сначала найдем координаты векторов:

Для этого нужно из координат конца вектора вычесть координаты начала вектора:

\(\vec{a}(11-4;10-3) \Rightarrow \ \ \ \vec{a}(7;7) \)

\(\vec{b}(15-4;3-3) \Rightarrow \ \ \ \vec{b}(11;0) \)

\( cos \ \alpha = \dfrac{x_1 \cdot x_2+y_1\cdot y_2 } { \sqrt {x_{1}^2+y_{1}^2}\cdot \sqrt {x_{2}^2+y_{2}^2} } \)

\( cos \ \alpha = \dfrac{7 \cdot 11+7 \cdot 0 } { \sqrt {7^2+7^2}\cdot \sqrt {11^2+0^2} } =\dfrac{77}{ \sqrt {98}\cdot \sqrt {11^2} } \)

\( cos \ \alpha = \dfrac{77}{ \sqrt {98}\cdot 11} \)

\( cos \ \alpha = \dfrac{7}{ \sqrt {49 \cdot 2}} \)

\( cos \ \alpha = \dfrac{7}{7 \sqrt { 2}} \)

\( cos \ \alpha = \dfrac{1}{ \sqrt { 2}} \)

Домножим на \( \sqrt { 2} \) числитель и знаменатель:

\( cos \ \alpha = \dfrac{ \sqrt { 2}}{2} \)

косинус какого угла равен \( \dfrac{ \sqrt { 2}}{2} \ \ ? \)

Ответ: \( 45^0 \)

ПОЗЖЕ

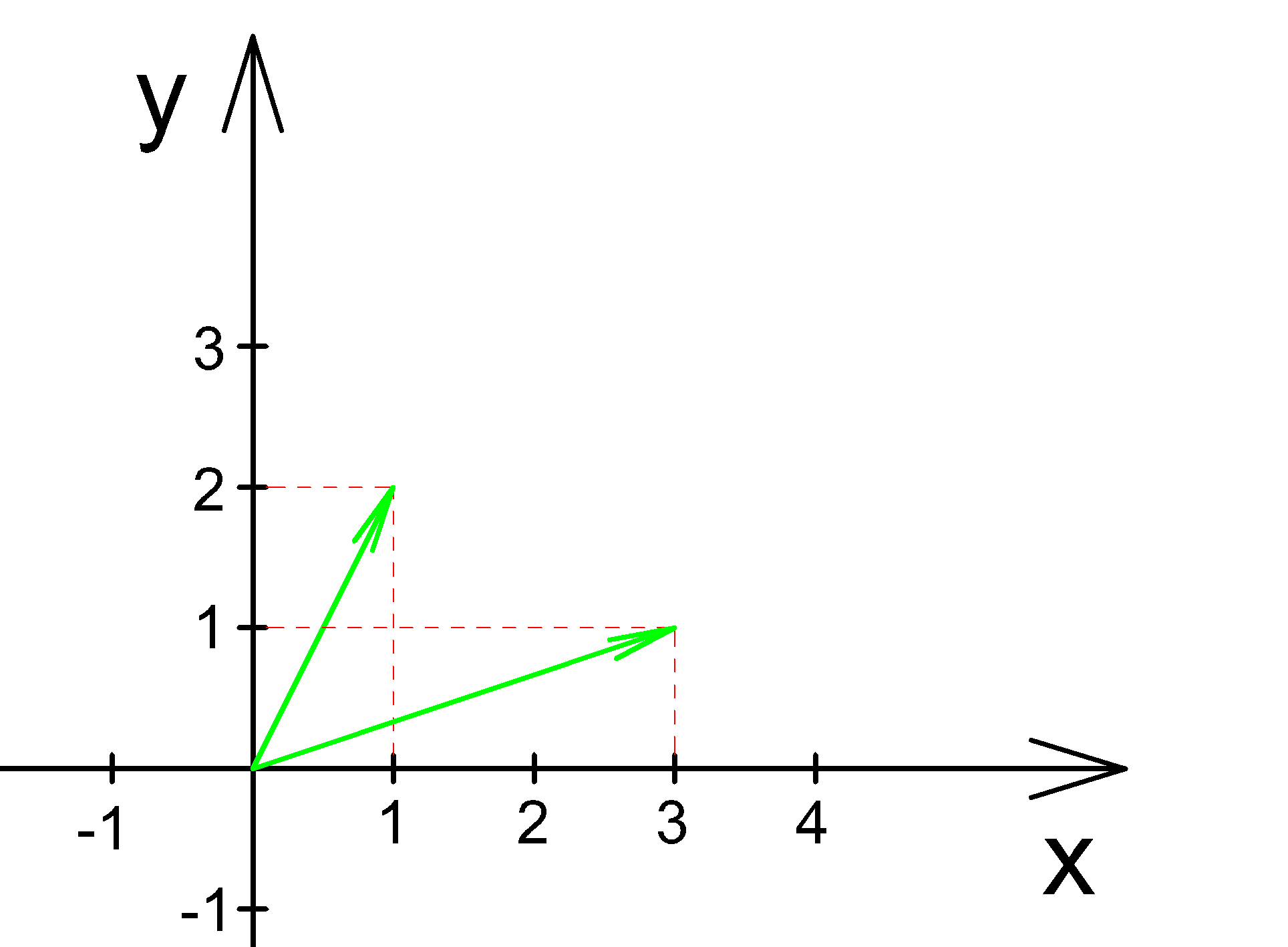
2. Найти угол между векторами изображенными на рисунке
Показать ответ Показать решение Видеорешение

Ответ: \( 45^0 \)

Сначала найдем координаты векторов:

Для этого нужно из координат конца вектора вычесть координаты начала вектора:

\(\vec{a}(1-0;2-0) \Rightarrow \ \ \ \vec{a}(1;2) \)

\(\vec{b}(3-0;1-0) \Rightarrow \ \ \ \vec{b}(3;1) \)

\( cos \ \alpha = \dfrac{x_1 \cdot x_2+y_1\cdot y_2 } { \sqrt {x_{1}^2+y_{1}^2}\cdot \sqrt {x_{2}^2+y_{2}^2} } \)

\( cos \ \alpha = \dfrac{1 \cdot 3+2 \cdot 1 } { \sqrt {1^2+2^2}\cdot \sqrt {3^2+1^2} } =\dfrac{5}{ \sqrt {5}\cdot \sqrt {10} } \)

\( cos \ \alpha = \dfrac{5}{ \sqrt {5}\cdot \sqrt {5} \cdot \sqrt {2} } \)

\( cos \ \alpha = \dfrac{5}{ 5 \sqrt {2} } \)

\( cos \ \alpha = \dfrac{1}{ \sqrt { 2}} \)

Домножим на \( \sqrt { 2} \) числитель и знаменатель:

\( cos \ \alpha = \dfrac{ \sqrt { 2}}{2} \)

косинус какого угла равен \( \dfrac{ \sqrt { 2}}{2} \ \ ? \)

Ответ: \( 45^0 \)

ПОЗЖЕ