Теорема косинусов
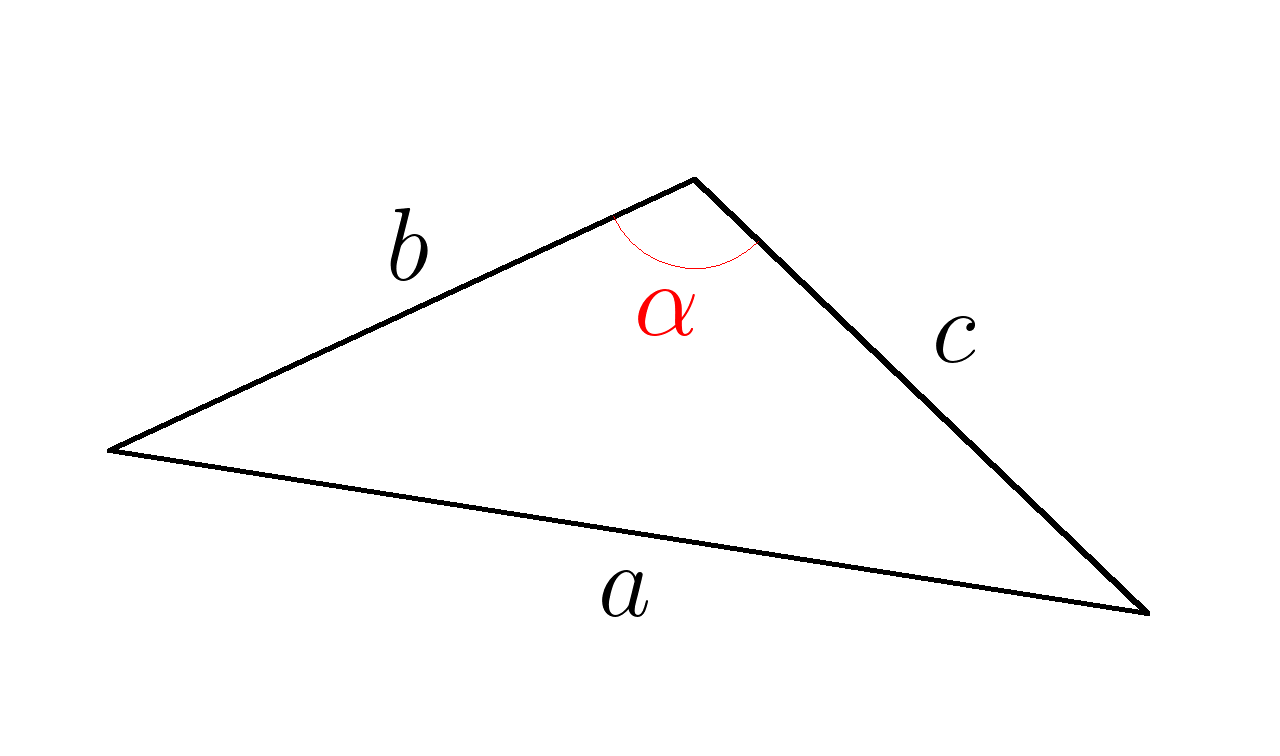
Для любого треугольника справедливо следующее соотношение:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
Квадрат стороны треугольника равен сумме квадратов двух других сторон вычесть удвоенное произведение
этих сторон на косинус угла между ними.
Кликнув по этому тексту мы сразу перейдем
к задачам на нахождение угла по трем сторонам треугольника, используя теорему косинусов
Репетитор по геометрии, физике и математике
8 916 478 10 32
Простейшие задачи на теорему косинусов:
Задача 1. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке \( b=7 , c=15, \alpha=60^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=7^2+15^2-2 \cdot 7 \cdot 15 \cdot cos \;\; 60^0 \)
\( a^2=49+225-2 \cdot 7 \cdot 15 \cdot 0,5 \)
\( a^2=274- 7 \cdot 15 \)
\( a^2=274- 105 \)
\( a^2=169 \)
\( a=13 \)
Ответ: \( a=13 \)
Репетитор по геометрии
8 916 478 10 32
Задача 2. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке \( b=3 , \; c=8, \; \alpha=60^0 ,\; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=3^2+8^2-2 \cdot 3 \cdot 8 \cdot cos \;\; 60^0 \)
\( a^2=9+64-2 \cdot 3 \cdot 8 \cdot 0,5 \)
\( a^2=73- 3 \cdot 8 \)
\( a^2=73- 24 \)
\( a^2=49 \)
\( a=7 \)
Ответ: \( a=7 \)
Задача 3. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке \( b=6 , \; c=16, \; \alpha=60^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=6^2+16^2-2 \cdot 6 \cdot 16 \cdot cos \;\; 60^0 \)
\( a^2=36+256-2 \cdot 6 \cdot 16 \cdot 0,5 \)
\( a^2=292- 6 \cdot 16 \)
\( a^2=292-96 \)
\( a^2=196 \)
\( a=14 \)
Ответ: \( a=14 \)

4. В треугольнике, изображенном на рисунке \( b=2 , \; c=\sqrt{3}, \; \alpha=30^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=2^2+(\sqrt{3})^2-2 \cdot 2 \cdot \sqrt{3} \cdot cos \;\; 30^0 \)
\( a^2=4+3-2 \cdot 2 \cdot \sqrt{3} \cdot \dfrac{\sqrt{3}}{2} \)
\( a^2=7-2 \cdot 3 \)
\( a^2=7-6 \)
\( a^2=1 \)
\( a=1 \)
Ответ: \( a=1 \)

5. В треугольнике, изображенном на рисунке \( b=4 , \; c=2\sqrt{3}, \; \alpha=30^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=4^2+(2\sqrt{3})^2-2 \cdot 4 \cdot 2\sqrt{3} \cdot cos \;\; 30^0 \)
\( a^2=16+4\cdot3-2 \cdot 4 \cdot 2\sqrt{3} \cdot \dfrac{\sqrt{3}}{2} \)
\( a^2=16+12-8 \sqrt{3} \cdot \sqrt{3} \)
\( a^2= 28-24 \)
\( a^2=4 \)
\( a=2 \)
Ответ: \( a=2 \)

6. В треугольнике, изображенном на рисунке \( a=13 , c=15, \alpha=60^0 , \; \) найти сторону \(b . \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( b_1=7 \;\;\; ; \;\;\;b_2=8 \)
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 13^2=b^2+15^2-2 \cdot b \cdot 15 \cdot cos \;\; 60^0 \)
\( 169=b^2+15^2-2 \cdot b \cdot 15 \cdot 0,5 \)
\(169=b^2+225-15b \)
\(b^2+225-15b-169=0 \)
\(b^2-15b+56=0 \)
\(D=(-15)^2-4\cdot 1\cdot 56=225-224=1\)
\(b_1=\dfrac{-(-15)+\sqrt{1}}{2}=8\)
\(b_2=\dfrac{-(-15)-\sqrt{1}}{2}=7\)
эта задача имеет два решения, сторона \(b\) может равняться как семи так и восьми,
если мы подставим вместо \(b\) семь или восемь в формулу теоремы косинусов , то оба эти ответа будут справедливыми.
Ответ: \( b_1=7 \;\;\; ; \;\;\;b_2=8 \)

7. В треугольнике, изображенном на рисунке \(a=7, \; b=3 , \; \alpha=60^0 , \; \) найти сторону \(c . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 7^2=3^2+c^2-2 \cdot 3 \cdot c \cdot cos \;\; 60^0 \)
\( 49=9+c^2-2 \cdot 3 \cdot c \cdot 0,5 \)
\(49-9=c^2-3c \)
\(40=c^2-3c \)
\(c^2-3c-40=0 \)
\(D=(-3)^2-4 \cdot 1 \cdot (-40)=9+160=169 \)
\( c_1=\dfrac{-(-3)+\sqrt{169}}{2}= \dfrac{3+13}{2}= 8 \)
\( c_2=\dfrac{-(-3)-\sqrt{169}}{2}= \dfrac{3-13}{2}= -5 \)
\(с_2=-5 \) не удовлетворяет условию задачи, так как сторона треугольника не может быть отрицательной
Ответ: \( с=8 \)

8. В треугольнике, изображенном на рисунке \(a=14, \; b=6 , \; \alpha=60^0 , \; \) найти сторону \(c . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 14^2=6^2+c^2-2 \cdot 6 \cdot c \cdot cos \;\; 60^0 \)
\( 196=36+c^2-2 \cdot 6 \cdot c \cdot 0,5 \)
\(196-36=c^2-6c \)
\(160=c^2-6c \)
\(c^2-6c-160=0 \)
\(D=(-6)^2-4 \cdot 1 \cdot (-160)=36+640=676 \)
\( c_1=\dfrac{-(-6)+\sqrt{676}}{2}= \dfrac{6+26}{2}=16 \)
\( c_2=\dfrac{-(-6)-\sqrt{676}}{2}= \dfrac{6-26}{2}=-10 \)
\(с_2=-10 \) не удовлетворяет условию задачи, так как сторона треугольника не может быть отрицательной
Ответ: \( c=16 \)

9. В треугольнике, изображенном на рисунке \(a=1, \; c=\sqrt{3} , \; \alpha=30^0 , \; \) найти сторону \(b . \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( b_1=2 \;\;\; ; \;\;\;b_2=1 \)
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 1^2=b^2+(\sqrt{3})^2-2 \cdot b \cdot \sqrt{3} \cdot cos \;\; 30^0 \)
\( 1=b^2+3-2 \cdot b \cdot \sqrt{3} \cdot \dfrac{\sqrt{3}}{2} \)
\( 1-3=b^2- b \cdot \sqrt{3} \cdot \sqrt{3} \)
\( -2=b^2- b \cdot 3 \)
\( b^2- 3b+2=0 \)
\(D=(-3)^2-4 \cdot 1 \cdot 2=9-8=1 \)
\( b_1=\dfrac{-(-3)+\sqrt{1}}{2}= \dfrac{3+1}{2}=2 \)
\( b_2=\dfrac{-(-6)-\sqrt{676}}{2}= \dfrac{3-1}{2}=1 \)
эта задача имеет два решения, сторона \(b\) может равняться как двум так и одному,
если мы подставим вместо \(b\) два или один в формулу теоремы косинусов , то оба эти ответа будут справедливыми.
Ответ: \( b_1=2 \;\;\; ; \;\;\;b_2=1 \)

15. В треугольнике, изображенном на рисунке \( b=4 , c=2+\sqrt{37}, \alpha=60^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=4^2+(2+\sqrt{37})^2-2 \cdot 4 \cdot (2+\sqrt{37}) \cdot cos \;\; 60^0 \)
\( a^2=16+4+2\cdot 2\cdot \sqrt{37}+37 -2 \cdot 4 \cdot (2+\sqrt{37}) \cdot 0,5 \)
\( a^2=20+4 \sqrt{37}+37 - 4 \cdot (2+\sqrt{37}) \)
\( a^2=57+4 \sqrt{37} - 8-4\sqrt{37} \)
\( a^2=49 \)
\( a=7 \)
Ответ: \( a=7 \)

16. В треугольнике, изображенном на рисунке \( b=5\sqrt{2} , c=5+\sqrt{11}, \alpha=30^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=(5\sqrt{2})^2+(5+\sqrt{11})^2-2 \cdot 5\sqrt{2} \cdot (5+\sqrt{11}) \cdot cos \;\; 45^0 \)
\( a^2=25 \cdot 2+ 25+2\cdot 5 \cdot \sqrt{11}+11 -2 \cdot 5\sqrt{2} \cdot (5+\sqrt{11}) \cdot \dfrac{\sqrt{2}}{2} \)
\( a^2=50+ 25+10 \sqrt{11}+11 - 5\sqrt{2} \cdot (5+\sqrt{11}) \cdot \sqrt{2} \)
\( a^2=86+10 \sqrt{11} - 5\cdot 2 \cdot (5+\sqrt{11}) \)
\( a^2=86+10 \sqrt{11} - 10 \cdot (5+\sqrt{11}) \)
\( a^2=86+10 \sqrt{11} - 50- 10 \sqrt{11} \)
\( a^2=36 \)
\( a=6 \)
Ответ: \( a=6 \)
Задача 20. (Решить задачу, применив теорему косинусов)
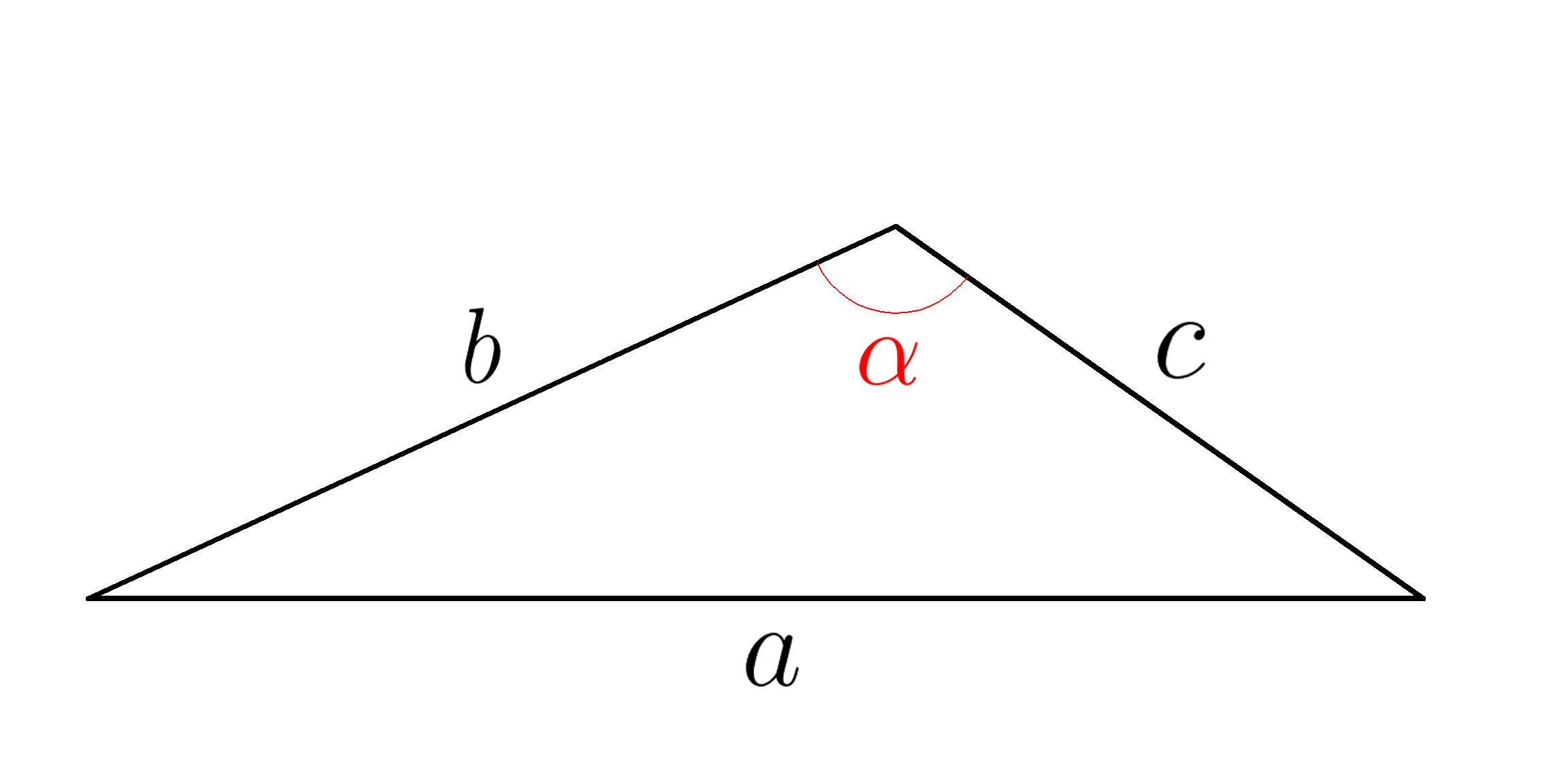
В треугольнике, изображенном на рисунке \( b=35 , c=21, \alpha=120^0 , \; \) найти сторону \(a . \)
Показать ответ
Показать решение
Видеорешение
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( a^2=35^2+21^2-2 \cdot 35 \cdot 21 \cdot cos \;\; 120^0 \)
\( a^2=1225+441-2 \cdot 35 \cdot 21 \cdot (-0,5) \)
\( a^2=1666 +35 \cdot 21 \)
\( a^2=1666 +735 \)
\( a^2= 2401 \)
\( a_1= 49 \;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\; a_2= -49 \;не \; подходит\)
Ответ: \( a=49 \)
Задачи на нахождение угла по трем сторонам треугольника
с применением теоремы косинусов
Задача 22. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке \(a=13, b=7 , c=15 , \; \) найти угол \(\alpha . \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( \alpha = 60^0 \)
Для нахождения угла \(\alpha \) сначала вычислим его косинус, с помощью теоремы косинусов.
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 13^2=7^2+15^2-2 \cdot 7 \cdot 15 \cdot cos \;\; \alpha \)
\( 169=49+225-2 \cdot 7 \cdot 15 \cdot cos \;\; \alpha \)
\(169=274-210 \cdot cos \;\; \alpha \)
\(169-274=-210 \cdot cos \;\; \alpha \)
\(−105=-210 \cdot cos \;\; \alpha \)
\(\dfrac{-105}{-210}= cos \;\; \alpha \)
\(0,5= cos \;\; \alpha \)
\( cos \;\; \alpha =0,5 \)
Косинус какого угла равен \(0,5 ?\)
Косинус \(60^0\) равен \(0,5 \)
значит угол \( \alpha = 60^0 \)
Ответ: \( \alpha = 60^0 \)
Задача 23. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке \(a=7, b=3 , c=8 , \; \) найти угол \(\alpha . \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( \alpha = 60^0 \)
Для нахождения угла \(\alpha \) сначала вычислим его косинус, с помощью теоремы косинусов.
Запишем теорему косинусов для этой задачи:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
\( 7^2=3^2+8^2-2 \cdot 3 \cdot 8 \cdot cos \;\; \alpha \)
\( 49=9+64-48 \cdot cos \;\; \alpha \)
\( 49-9-64=-48 \cdot cos \;\; \alpha \)
\( -24=-48 \cdot cos \;\; \alpha \)
\( \dfrac{-24}{-48}= cos \;\; \alpha \)
\(0,5= cos \;\; \alpha \)
\( cos \;\; \alpha =0,5 \)
Косинус какого угла равен \(0,5 ?\)
Косинус \(60^0\) равен \(0,5 \)
значит угол \( \alpha = 60^0 \)
Ответ: \( \alpha = 60^0 \)














