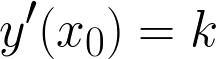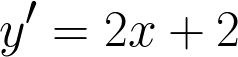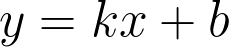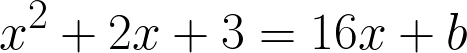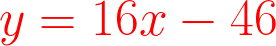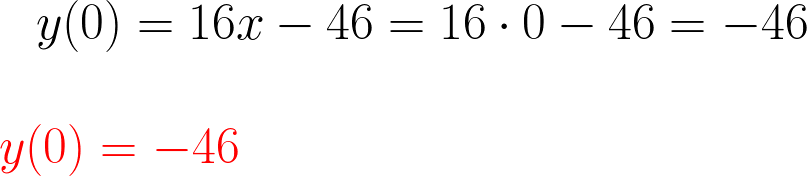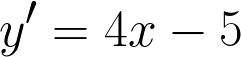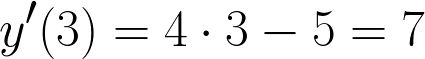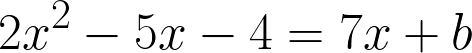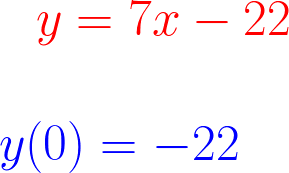Геометрический смысл производной.
Производная функции в точке касания равна угловому коэффициенту касательной.
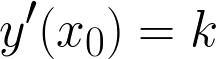
1. Для функции \(y=x^2+2x+3\) написать уравнение касательной в точке \(x_0=7\) .
В ответе записать ординату этой касательной в точке \(x = 0\)
Показать ответ
Показать решение
Решение:
Продифференицируем функцию:
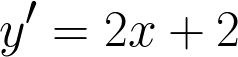
Найдем значение производной в точке касания:


Касательная это прямая, поэтому ее уравнение в общем виде:
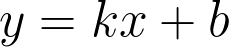
Наша парабола и касательная пересекаются, поэтому приравняем правые части, вставив вместо углового коэффициента 16
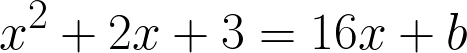
абсцисса касания равна 7, поэтому вместо x мы вставим 7

Уравнение касательной в точке 7:
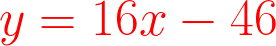
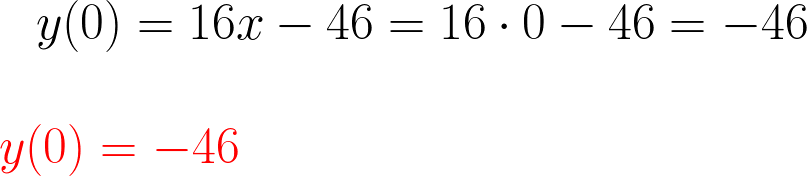
2. Для функции:

Написать уравнение касательной в точке x = 3 .
В ответе записать ординату этой касательной в точке x = 0
Показать ответ
Показать решение
Решение:
Продифференицируем функцию:
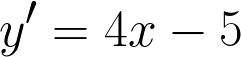
Найдем значение производной в точке касания:
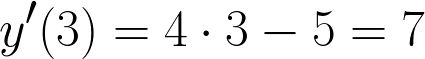

Касательная это прямая, поэтому ее уравнение в общем виде:
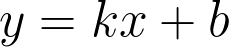
Наша парабола и касательная пересекаются, поэтому приравняем правые части, вставив вместо углового коэффициента 7
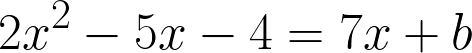
абсцисса касания равна 3, поэтому вместо x мы вставим 3

Уравнение касательной к параболе в точке 3:
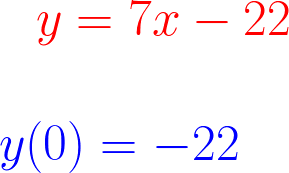

3. Прямая \(y=9x+2\) параллельна касательной к графику \(f(x)=x^2+5x-3\) .Найти абсциссу точки касания
Показать ответ
Показать решение
Решение:
Прямая \(y=9x+2\) и касательная параллельны, значит угловой коэффициент касательной тоже равен 9 \((k=9)\).
По геометрическому смыслу производной:
\(f{}'(x_0)=k=9\)
\(x_0\) это абсцисса касания
Продифференцируем функцию:
\(f{}'(x)=2x+5\)
\(f{}'(x_0)=2x_0+5=9\)
\(2x_0+5=9\)
\(x_0=2\)
4. Прямая \(y=6x-5\) является касательной к графику \(f(x)=x^3+2x^2-x+d\) .Найти \(d\) , если абсцисса точки касания
положительна.
Показать ответ
Показать решение
Решение:
Продифференцируем функцию:
\(f{}'(x)=3x^2+4x-1\)
\(f{}'(x_0)=3x_0^2+4x_0-1=6\)
\(3x_0^2+4x_0-7=0 \)
\(D=16-4\cdot(-7)\cdot 3=16+84=100 \)
\(x_0=\frac{-4+10}{6}=1\)
\(x_0=\frac{-4-10}{6}=-\frac{7}{3}\)
\(x_0>0\) значит \(x_0=1\)
Приравниваем правые части уравнений:
\(x^3+2x^2-x+d=6x-5\)
вместо \(x\) вставляем \(1:\)
\(1^3+2\cdot1^2-1+d=6\cdot1-5\)
\(2+d=1\)
\(d=-1\)
5. Прямая \(y=32x-42\) является касательной к графику \(f(x)=ax^2+2x+3\) .Найти \(a\) .
Показать ответ
Показать решение
Решение:
Продифференцируем функцию:
\(f{}'(x)=2ax+2\)
\(f{}'(x_0)=2ax_0+2=32\)
\begin{cases}
2ax_0+2=32 \\
ax_0^2+2x_0+3=32x_0-42
\end{cases} \begin{cases}
2ax_0=30 \\
ax_0^2-30x_0+45=0
\end{cases} \begin{cases}
x_0=\frac{30}{2a} \\
ax_0^2-30x_0+45=0
\end{cases} \begin{cases}
x_0=\frac{15}{a} \\
ax_0^2-30x_0+45=0
\end{cases}
\(a\cdot(\frac{15}{a})^2-30\cdot\frac{15}{a}+45=0\)
\(a\cdot\frac{225}{a^2}-\frac{450}{a}+45=0\)
\(\frac{5}{a}-\frac{10}{a}+1=0\)
\(-\frac{5}{a}+1=0\)
\(a=5 \)