Коэффициент полезного действия (КПД).
КПД равен отношению (делению) полезной работы к затраченной
\( \eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% \)
1. Определить
КПД процесса, если полезная работа оказалась равна 100 Дж, а затраченная работа 200 Дж.
Показать ответ
Показать решение
Видеорешение
Дано:
\(A_{полезная}=100 Дж\)
\(A_{затраченная}=200 Дж\)
\(\eta-?\)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% =\dfrac{100Дж}{200Дж} \cdot 100 \%=50\% \)
Ответ: \(\eta= 50 \% \)
ПОЗЖЕ
2. Груз массой \(m=1 кг \) подняли на высоту \(h=10 м, \; \) при этом затраченная работа
оказалась равна 200 Дж .Определить КПД процесса.
Показать ответ
Показать решение
Видеорешение
Дано:
\(m=1 кг \)
\(A_{затраченная}=200 Дж\)
\(h=10 м \)
\(\eta-?\)
\( A_{полезная}=F \cdot S= m \cdot g\cdot S= m \cdot g\cdot h=1 кг \cdot 10 \dfrac{Н}{кг}\cdot 10 м=100 Дж \)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% =\dfrac{100Дж}{200Дж} \cdot 100 \%=50\% \)
Ответ: \(\eta= 50 \% \)
ПОЗЖЕ
3. Груз массой \(m=2 кг \) подняли на высоту \(h=15 м, \; \) при этом затраченная работа
оказалась равна 400 Дж .Определить КПД процесса.
Показать ответ
Показать решение
Видеорешение
Дано:
\(m=2 кг \)
\(A_{затраченная}=400 Дж\)
\(h=15 м \)
\(\eta-?\)
\( A_{полезная}=F \cdot S= m \cdot g\cdot S= m \cdot g\cdot h=2 кг \cdot 10 \dfrac{Н}{кг}\cdot 15 м=300 Дж \)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% =\dfrac{300Дж}{400Дж} \cdot 100 \%=75\% \)
Ответ: \(\eta= 75 \% \)
ПОЗЖЕ
4.Небольшую строительную плиту равномерно поднимают с помощью длинного рычага
на высоту \(h=0,3 \ м \). Затраченная при этом работа составила 400 Джоулей.
Какова масса плиты, если КПД этого механизма равен 90 процентов?
Показать ответ
Показать решение
Видеорешение
Дано:
\(\eta=90 \% \)
\(A_{затраченная}=400 \ Дж \)
\(h=0,3 м \)
\(g=10 \ \dfrac{Н}{кг} \)
\(m-?\)
\( A_{полезная}=F \cdot S= m \cdot g\cdot S= m \cdot g\cdot h \)
\( m=\dfrac{A_{полезная}}{gh} \)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% \)
\( A_{полезная}=\dfrac{\eta\cdot A_{затраченная}}{100 \% } \)
\( A_{полезная}=\dfrac{90 \% \cdot 400 \ Дж}{100 \% }=360 \ Дж \)
\( m=\dfrac{3600 \ Дж}{10 \ \dfrac{Н}{кг} \cdot 0,3 м }=120 \ кг \)
Ответ: \( m=120 \ кг \)
ПОЗЖЕ
5.
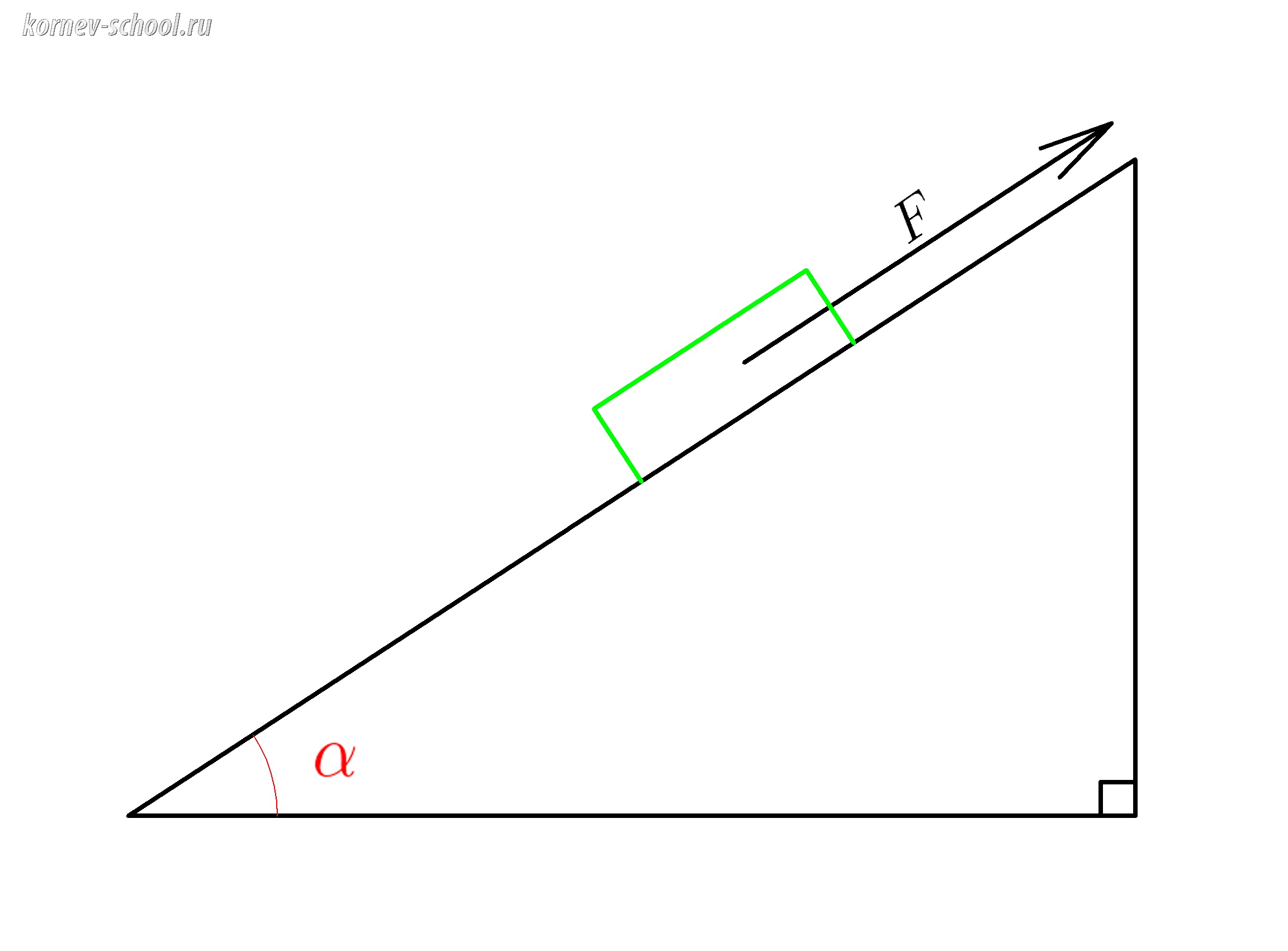
Наклонная плоскость имеет высоту \(h=0,9 \ м \) и длину \(S=5 \ м \).
По этой наклонной плоскости медленно втянули шкаф массой 80 кг, прикладывая силу 200 Ньютонов.
Вычислите КПД наклонной плоскости для этого процесса.
Показать ответ
Показать решение
Видеорешение
Дано:
\( S=5 \ м \)
\( F_{прикладываемая}=200 \ Н \)
\( m=80 \ кг \)
\(h=0,9 м \)
\(g=10 \ \dfrac{Н}{кг} \)
\(\eta-?\)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% \)
\( A_{полезная}=F_{тяжести} \cdot h= m \cdot g\cdot h \)
\( A_{полезная}= 80 \ кг\cdot 10 \ \dfrac{Н}{кг}\cdot 0,9 м=720 \ Дж \)
\( A_{затраченная}=F_{прикладываемая} \cdot S \)
\( A_{затраченная}=200 \ Н \cdot 5 \ м =1000 \ Дж \)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% =\dfrac{720 \ Дж}{1000 \ Дж} \cdot 100 \%=72 \% \)
Ответ: \( \eta= 72 \% \)
ПОЗЖЕ
6.
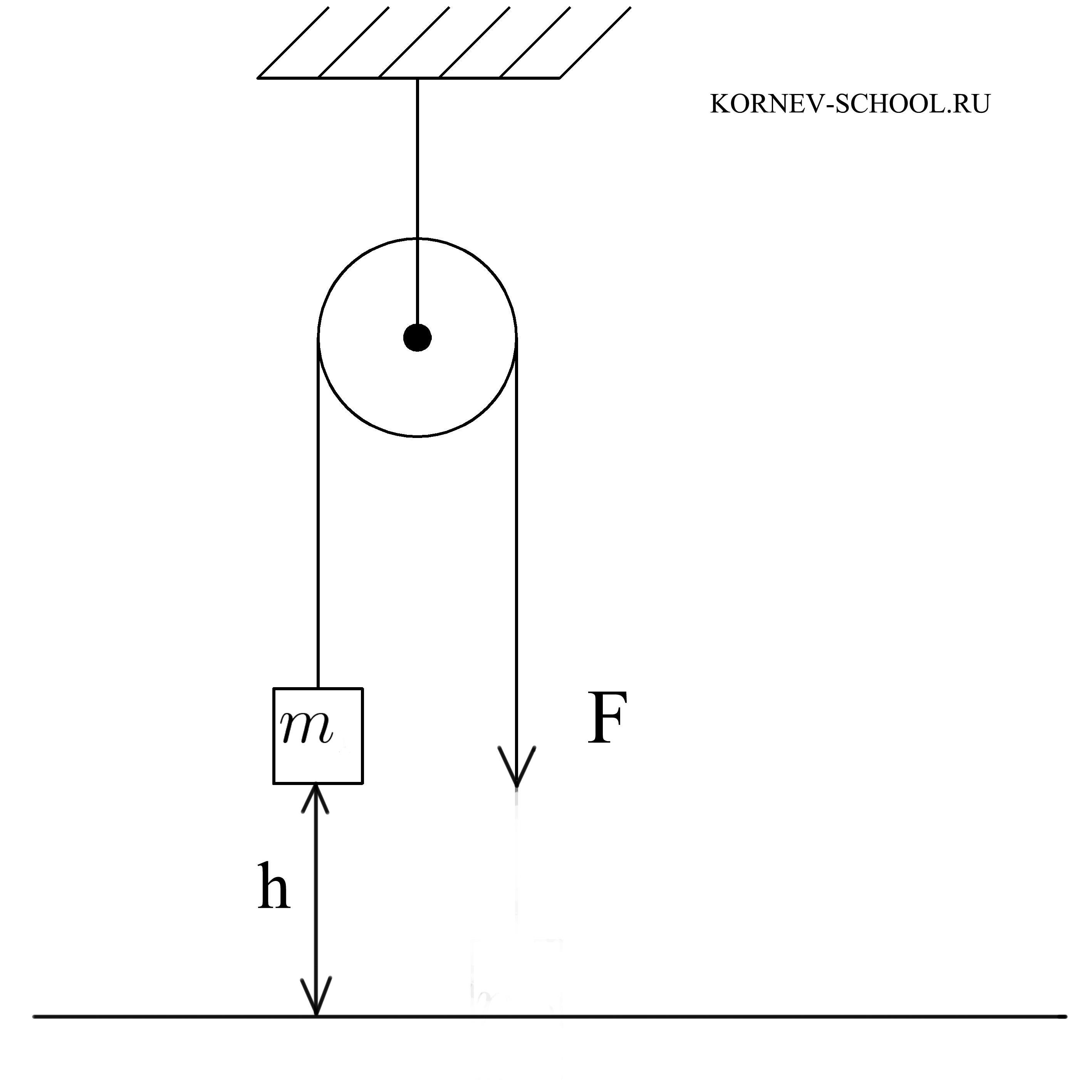
Груз массой 3 кг медленно подняли с помощью неподвижного блока на какую-то высоту.
Во время подъема этого груза к противоположному концу тросса прикладывали силу 40 Ньтонов.
Определите, чему равен КПД этого блока.
Почему не важно на какую именно высоту был поднят груз?
Показать ответ
Показать решение
Видеорешение
Неподвижный блок не дает выигрыша в силе, поэтому на сколько поднялся груз,
на столько и опустился правый конец тросса. \(h=S\)
Дано:
\( F_{прикладываемая}=40 \ Н \)
\( m=3 \ кг \)
\(g=10 \ \dfrac{Н}{кг} \)
\(\eta-?\)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% \)
\( A_{полезная}=F_{тяжести} \cdot h= m \cdot g\cdot h \)
\( A_{затраченная}=F_{прикладываемая} \cdot h \)
\( \eta=\dfrac{m \cdot g\cdot h} {F_{прикладываемая} \cdot h} \cdot 100 \% \)
\(h \) есть и в числителе и в знаменателе, в данном случае мы можем ее сократить
\( \eta=\dfrac{m \cdot g} {F_{прикладываемая}} \cdot 100 \% \)
\( \eta=\dfrac{3 \ кг \cdot 10 \ \dfrac{Н}{кг}} {40 \ Н} \cdot 100 \% = 75 \% \)
Ответ: \( \eta= 75 \% \)
ПОЗЖЕ
7.

Мальчик медленно поднялся в горку длиной 40 метров, таща за собой снегокат на веревке. Масса снегоката 10 кг.
Во время подъема мальчик тянул снегокат с силой \( F_{1}=25 \ Н \). КПД всего процесса составляет 85 % .
Найдите высоту горки.
Показать ответ
Показать решение
Другое решение
На самом деле всегда удобнее работать с долями, а не с процентами.
КПД тоже можно мерить не в процентах, а в долях.
85 %=0,85
Дано:
\( S=40 \ м \)
\( F_{1}=25 \ Н \)
\( m=10 \ кг \)
\(\eta=0,85 \)
\(g=10 \ \dfrac{Н}{кг} \)
\( h-?\)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \)
\( A_{полезная}=F_{тяжести} \cdot h= m \cdot g\cdot h \)
\( A_{затраченная}=F_{1} \cdot S \)
\(\eta=\dfrac{m \cdot g\cdot h}{F_{1} \cdot S} \)
Домножим обе части уравнения на знаменатель:
\(\eta \cdot F_{1} \cdot S = m \cdot g\cdot h \)
а теперь разделим обе части на \(mg\)
\(\dfrac{\eta \cdot F_{1} \cdot S}{mg}=h \)
\(h=\dfrac{\eta \cdot F_{1} \cdot S}{mg} \)
\(h=\dfrac{0,85 \cdot 25 \ Н \cdot 40 \ м}{10 \ кг \cdot 10 \ \dfrac{Н}{кг} } =8,5 \ м \)
Ответ: \( h= 8,5 \ м \)
\( A_{затраченная}=F_{1} \cdot S=25 \ Н \cdot 40 \ м=1000 \ Дж \)
\(\eta=\dfrac{A_{полезная}}{A_{затраченная}} \cdot 100 \% \)
\(85 \%=\dfrac{A_{полезная}}{1000 \ Дж } \cdot 100 \% \)
\( A_{полезная}=850 \ Дж \)
\( A_{полезная}= m \cdot g\cdot h \)
\( 850 = 10 \cdot 10\cdot h \)
\( h=8,5 \ м \)
Ответ: \( h= 8,5 \ м \)


