Разные задачи на динамику .

Задача 1:

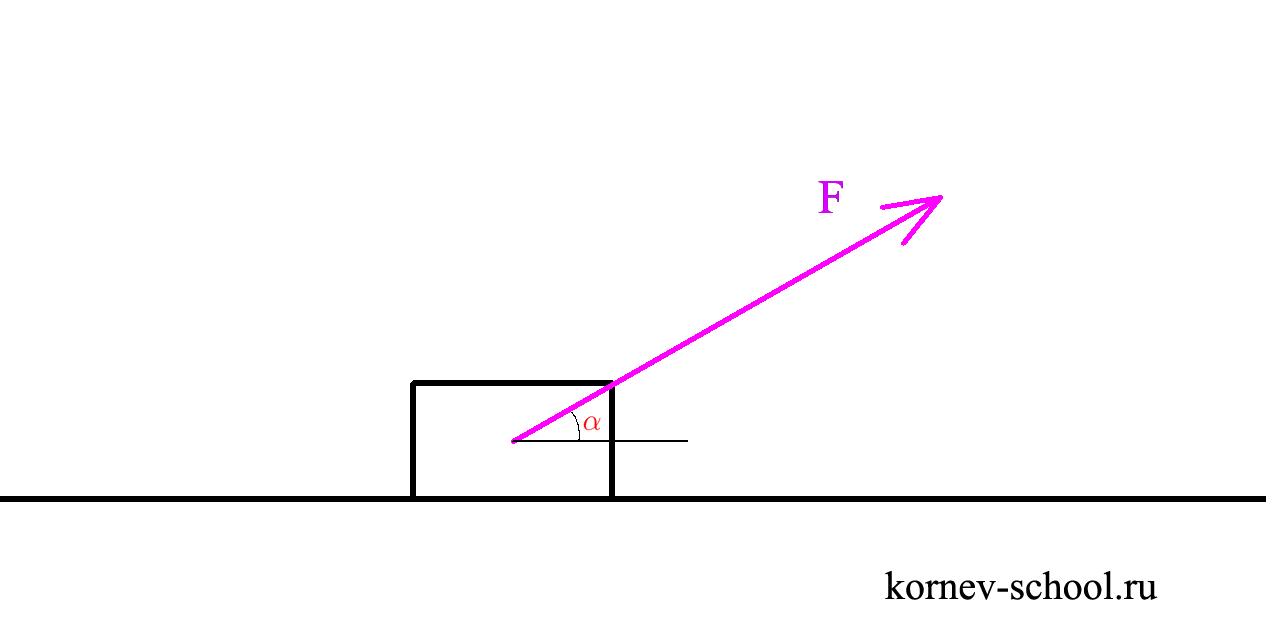
На горизонтальной поверхности покоится предмет массой \( m=2 \ кг \), коэффициент трения между поверхностью и предметом \( \mu=0,3 \). В какой-то момент к предмету прикладывают силу \(F=10 \sqrt{2} \ Н \), причем сила направлена под углом \( \alpha=45^0 \) к горизонту. С каким ускорением будет двигаться предмет вдоль поверхности.
Показать ответ Показать решение Видеорешение

Сила \( F \) не лежит всецело ла какой-либо оси, поэтому необходимо найти проекцию силы \(F\) на ось абсцисс и ось ординат.
Нарисуем жирную зеленую точку вместо нашего тела, для того, чтобы габариты тела не мешали нам строить проекции силы \( F \) .
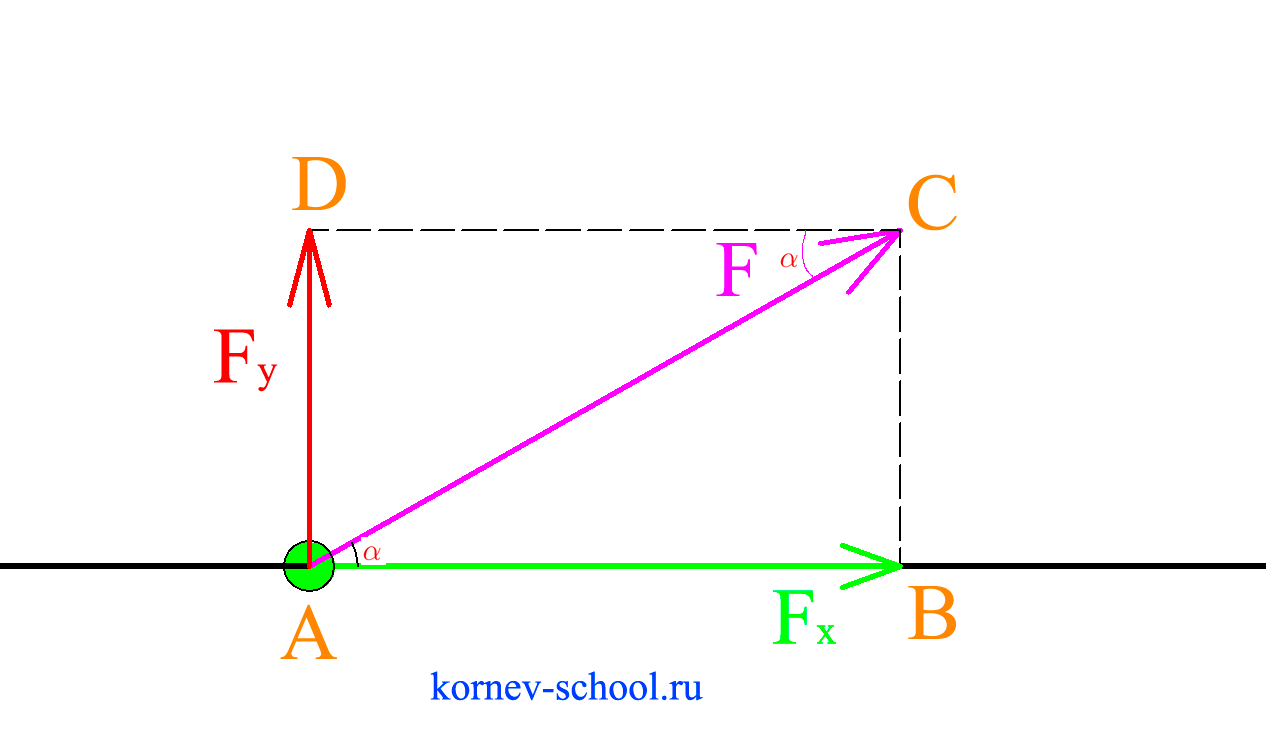Рассмотрим треугольник \(ABC\)

\( cos \ \alpha = \dfrac{F_x}{F} \)

\( F_x=F \cdot cos \ \alpha \)

\( \angle BAC=\angle ACD \) как накрест лежащие при параллельных прямых \(AB \ и \ DC \) и секущей \(AC\)

Рассмотрим треугольник \(ACD\) :

\(sin \ \alpha = \dfrac{F_y}{F} \)

\( F_y=F \cdot sin \ \alpha \)

Убререм с чертежа силу \( F \) и начертим ее проекции \( F_x \ и \ F_y \) и все остальные силы:
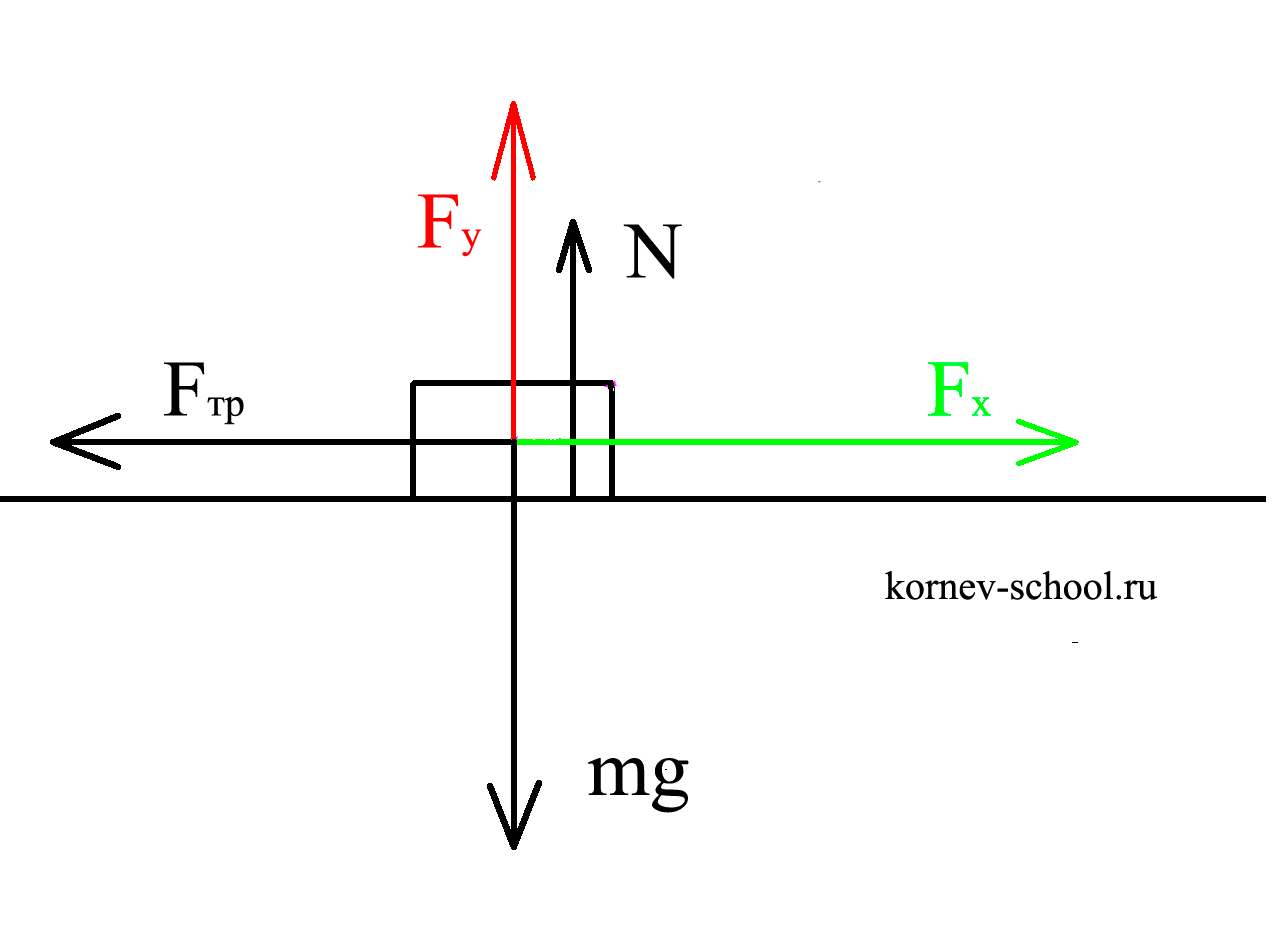Теперь мы может написать уравнение второго закона Ньютона на ось абсцисс и уравнение первого закона Ньютона на ось ординат, однако не будем торопиться и проверим сдвинет ли вообще проекция \(F_x \) наше тело, то есть выполняется ли условие: \(F_x > F_{тр}\)
Также нужно проверить условие \(F_y < mg\) в противном случае если проекция силы \(F\) на ось ординат будет больше чем сила тяжести, то тело просто взлетит и улетит в космос.

"x" \( \ \ \ \ F_x-F_{тр}=ma \)

\(F \cdot cos \ \alpha-\mu N=ma \)

\( a=\dfrac{F \cdot cos \ \alpha-\mu N}{m} \)

"y" \( \ \ \ \ F_y+N-mg=0 \)

\( F \cdot sin \ \alpha +N-mg=0 \)

\( N=mg-F \cdot sin \ \alpha \)

\( a=\dfrac{10 \sqrt{2} \ Н \cdot cos \ 45^0-0,3 (2 кг \cdot 10 \ м/с^2-10 \sqrt{2} \ Н \cdot sin \ 45^0)}{2 \ кг} \)

\( a=\dfrac{10 \sqrt{2} \ Н \cdot \dfrac{\sqrt{2}}{2}-0,3 (2 кг \cdot 10 \ м/с^2-10 \sqrt{2} \cdot \dfrac{\sqrt{2}}{2})}{2 \ кг} \)

\(a=3,5 \ м/с^2 \)

Ответ: \(a=3,5 \ м/с^2 \)