Кинематика .
\( a=\dfrac{v-v_0}{t} \)
В дальнейшем мы будем называть эту формулу "Первым уравнением кинематики"
\( a \) - ускорение
\(v_0 \) - начальная скорость
\(v \) - конечная скорость
\(t \) - время
Репетитор по физике
8 916 478 10 32
Задачи на кинематику(найти ускорение) .
1. Найти ускорение тела, если за время \(t= 10 \ \) секунд оно увеличивает свою скорость с \(v_0=10 \ м/с \) до \(v=30 \ м/с \)
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v=30 \ м/с \)
\(v_0=10 \ м/с \)
\(t=10 \ с \)
\(a-?\)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{30м/с-10м/с}{10с}=2 м/с^2 \)
Ответ: \(a=2м/с^2 \)
2. Автомобиль начинает движение из состояния покоя и за время \(t= 5 \ \) секунд он разгоняется до \(v=22 \ м/с \). С каким ускорением двигался автомобиль?
Показать ответ
Показать решение
Видеорешение
Ответ: \(a=4,4 \ м/с^2 \)
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v=22 \ м/с \)
\(v_0=0 \;м/с \)
\(t=5 \ с \)
\(a-?\)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{22м/с-0м/с}{5с}=4,4 м/с^2 \)
Ответ: \(a=4,4м/с^2 \)
3. Скорость автомобиля за 5 секунд уменьшается с \(v_0=25 \ м/с \) до \(v=5 \ м/с\). Найти проекцию ускорения автомобиля .
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v=5 \ м/с \)
\(v_0=25 \ м/с \)
\(t=5с \)
\(a-?\)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{5м/с-25м/с}{5с}=-4 м/с^2 \)
Ответ: \(a=-4м/с^2 \)
4. Скорость автомобиля за 5 секунд уменьшается с \(v_0=25 \ м/с \) до \(v=5 \ м/с\). Найти модуль ускорения автомобиля .
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v=5м/с \)
\(v_0=25 \;м/с \)
\(t=5с \)
\(|a|-?\)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{|5м/с-25м/с|}{5с}=4 м/с^2 \)
Ответ: \(|a|=4м/с^2 \)
5. Мотоцикл разгоняется из состояния покоя до скорости 72 км/ч за 10 секунд.Найти его ускорение.
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v = 72 км/ч \)
\(v_0=0м/с\)
\(t=10 c\)
\(a-?\)
СИ
\(v=20 м/с \)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{20м/с-0м/с}{10с}=2 м/с^2\)
Ответ: \(a=2 м/с^2 \)
6. Мотоцикл тормозит с \(v_0=54 км/ч \ до \ v=36 км/ч \ \) за 5 секунд.Найти проекцию его ускорения.
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v = 36 км/ч \)
\(v_0=54км/ч\)
\(t=5 c\)
\(a-?\)
СИ
\(v=10 м/с \)
\(v_0=15 м/с \)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{10м/с-15м/с}{5с}=-1 м/с^2\)
Ответ: \(a=-1 м/с^2 \)
7. Мотоцикл тормозит с \(v_0=68,4 км/ч \) до полной остановки за 38 секунд.Найти проекцию его ускорения.
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v = 0 м/с \)
\(v_0=68,4км/ч\)
\(t=38 c\)
\(a-?\)
СИ
\(v_0=19 м/с \)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{0м/с-19м/с}{38с}=-0,5 м/с^2\)
Ответ: \(a=-0,5 м/с^2 \)
8. Велосипедист разгоняется с \(v_0=3,6 км/ч \) до \(v=18 км/ч \) за 16 секунд.Найти проекцию его ускорения.
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v = 18км/ч \)
\(v_0=3,6км/ч\)
\(t=16 c\)
\(a-?\)
СИ
\(v=5 м/с \)
\(v_0=1 м/с \)
\(a=\dfrac{v-v_0}{t} \)
\(a=\dfrac{5м/с-1м/с}{16с}=0,25 м/с^2\)
Ответ: \(a=0,25 м/с^2 \)
9. Скутер разгоняется с \(v_0=7,2 км/ч \) до \(v=43,2 км/ч \) за 2,5 секунды.Найти модуль его ускорения.
Показать ответ
Показать решение
Видеорешение
Сначала запишем "Первое уравнение кинематики":
Дано:
\(v = 43,2км/ч \)
\(v_0=7,2км/ч\)
\(t=2,5 c\)
\(|a|-?\)
СИ
\(v=12 м/с \)
\(v_0=2 м/с \)
\(|a|=\dfrac{|v-v_0|}{t} \)
\(|a|=\dfrac{|12м/с-2м/с|}{2,5с}=4 м/с^2\)
Ответ: \(|a|=4 м/с^2 \)
Задачи на кинематику(найти скорость) .
10. Тело начинает движение из состояния покоя с ускорением \( 1 м/с^2 \),
какую скорость оно приобретет через 10 секунд?
Показать ответ
Показать решение
Видеорешение
\( a=\dfrac{v-v_0}{t} \;\;\;\;\;\;\;умножим\;\;обе\;\;части\;\;первого\;\; уравнения\;\;кинематики\;\; на\;\; время: \)
\( a\cdot t=\dfrac{v-v_0}{t}\cdot t \)
\(at=v-v_0\)
\(at+v_0=v\)
\(v=v_0+at\)
Дано:
\(a = 1 \;м/с^2 \)
\(v_0=0 \;м/с \)
\(t=10с \)
\(v-?\)
\(v=v_0+at \)
\(v=0+ 1 \;м/с^2 \cdot 10с = 10\;м/с \)
Ответ: \(v=10\;м/с \)
11. Поезд ,двигаясь со скоростью 5 м/с, начал разгоняться с ускорением \( 0,5 м/с^2 \),
с какой скоростью он будет двигаться через 10 секунд?
Показать ответ
Показать решение
Видеорешение
\( a=\dfrac{v-v_0}{t} \;\;\;\;\;\;\;умножим\;\;обе\;\;части\;\;первого\;\; уравнения\;\;кинематики\;\; на\;\; время: \)
\( a\cdot t=\dfrac{v-v_0}{t}\cdot t \)
\(at=v-v_0\)
\(at+v_0=v\)
\(v=v_0+at\)
Дано:
\(a = 0,5 \;м/с^2 \)
\(v_0=5 \;м/с \)
\(t=10с \)
\(v-?\)
\(v=v_0+at \)
\(v=5+ 0,5 \;м/с^2 \cdot 10с = 10\;м/с \)
Ответ: \(v=10\;м/с \)
12. Начальная скорость тела равна 10м/с, модуль ускорения равен \(|a|=1м/с^2 \).
Вектор ускорения направлен в сторону, противоположную направлению вектора начальной скорости.
Найти скорость тела через 3 секунды.
Показать ответ
Показать решение
Видеорешение
Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1
Если вектор начальной скорости и вектор ускорения разнонаправлены,то скорость тела будет уменьшаться, поэтому в первом уравнении кинематики поставим знак минус
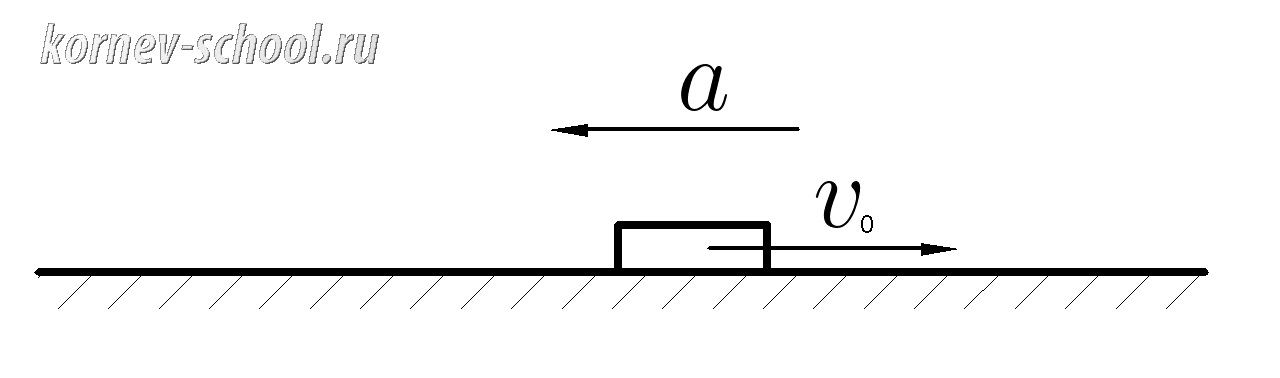\(v=v_0-at \)
Дано:
\(|a| = 1 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=3с \)
\(v-?\)
\(v=v_0-at \)
\(v=10- 1 \;м/с^2 \cdot 3с = 7\;м/с \)
Ответ: \(v=7\;м/с \)
Решение номер 2
Если вектор начальной скорости и вектор ускорения разнонаправлены,то проекция ускорения отрицательна, то есть если
\(|a|=1, то a=-1 \)
Дано:
\(a = -1 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=3с \)
\(v-?\)
\(v=v_0+at \)
\(v=10+ (-1 \;м/с^2) \cdot 3с = 7\;м/с \)
Ответ: \(v=7\;м/с \)
13. Начальная скорость тела равна 7м/с, модуль ускорения равен \(|a|=0,25м/с^2 \).
Вектор ускорения направлен в сторону, противоположную направлению вектора начальной скорости.
Найти скорость тела через 28 секунд.
Показать ответ
Показать решение
Видеорешение
Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1
Если вектор начальной скорости и вектор ускорения разнонаправлены,то скорость тела будет уменьшаться, поэтому в первом уравнении кинематики поставим знак минус
\(v=v_0-at \)
Дано:
\(|a| = 0,25 \;м/с^2 \)
\(v_0=7 \;м/с \)
\(t=28с \)
\(v-?\)
\(v=v_0-at \)
\(v=7- 0,25 \;м/с^2 \cdot 28с = 7\;м/с \)
Ответ: \(v=0\;м/с \)
Решение номер 2
Если вектор начальной скорости и вектор ускорения разнонаправлены,то проекция ускорения отрицательна, то есть если
\(|a|=0,25, то a=-0,25 \)
Дано:
\(a = -0,25 \;м/с^2 \)
\(v_0=7 \;м/с \)
\(t=28с \)
\(v-?\)
\(v=v_0+at \)
\(v=7+ (-0,25 \;м/с^2) \cdot 28с = 0\;м/с \)
Ответ: \(v=0\;м/с \)
14. Проекция начальной скорости тела равна 10м/с, модуль ускорения равен \(|a|=0,5м/с^2 \).
Вектор ускорения направлен в сторону, противоположную направлению вектора начальной скорости.
Найти проекцию скорости тела через 100 секунд.
Показать ответ
Показать решение
Видеорешение
Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1
Если вектор начальной скорости и вектор ускорения разнонаправлены,то скорость тела будет уменьшаться, поэтому в первом уравнении кинематики поставим знак минус
\(v=v_0-at \)
Дано:
\(|a| = 0,5 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=100с \)
\(v-?\)
\(v=v_0-at \)
\(v=10- 0,5 \;м/с^2 \cdot 100с = -40\;м/с \)
Ответ: \(v=-40\;м/с \)
Решение номер 2
Если вектор начальной скорости и вектор ускорения разнонаправлены,то проекция ускорения отрицательна, то есть если
\(|a|=0,5, то a=-0,5 \)
Дано:
\(a = -0,5 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=100с \)
\(v-?\)
\(v=v_0+at \)
\(v=10+ (-0,5 \;м/с^2) \cdot 100с = -40\;м/с \)
Ответ: \(v=-40\;м/с \)
15. Проекция начальной скорости тела равна 10м/с, модуль ускорения равен \(|a|=0,5м/с^2 \).
Вектор ускорения направлен в сторону, противоположную направлению вектора начальной скорости.
Найти модуль скорости тела через 100 секунд.
Показать ответ
Показать решение
Видеорешение
Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1
Если вектор начальной скорости и вектор ускорения разнонаправлены,то скорость тела будет уменьшаться, поэтому в первом уравнении кинематики поставим знак минус
\(v=v_0-at \)
Дано:
\(|a| = 0,5 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=100с \)
\(v-?\)
\(|v|=|v_0-at| \)
\(|v|=|10- 0,5 \;м/с^2 \cdot 100с| = 40\;м/с \)
Ответ: \(|v|=40\;м/с \)
Решение номер 2
Если вектор начальной скорости и вектор ускорения разнонаправлены,то проекция ускорения отрицательна, то есть если
\(|a|=0,5, то a=-0,5 \)
Дано:
\(a = -0,5 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(t=100с \)
\(v-?\)
\(|v|=|v_0+at| \)
\(|v|=|10+ (-0,5 \;м/с^2) \cdot 100с| = 40\;м/с \)
Ответ: \(|v|=40\;м/с \)
16. Вектор начальной скорости тела направлен против положительного направления оси абсцисс.
Вектор ускорения сонаправлен с ним.Проекция начальной скорости тела \(v_{0x}= -15м/с \) , проекция ускорения равна \(a_x=-0,5м/с^2 \). Найти проекцию скорости через 10 секунд.
Показать ответ
Показать решение
Видеорешение
Если вектор начальной скорости и вектор ускорения сонаправлены и направлены против положительного направления оси,то модуль скорости тела будет возрастать,а проекция скорости будет убывать
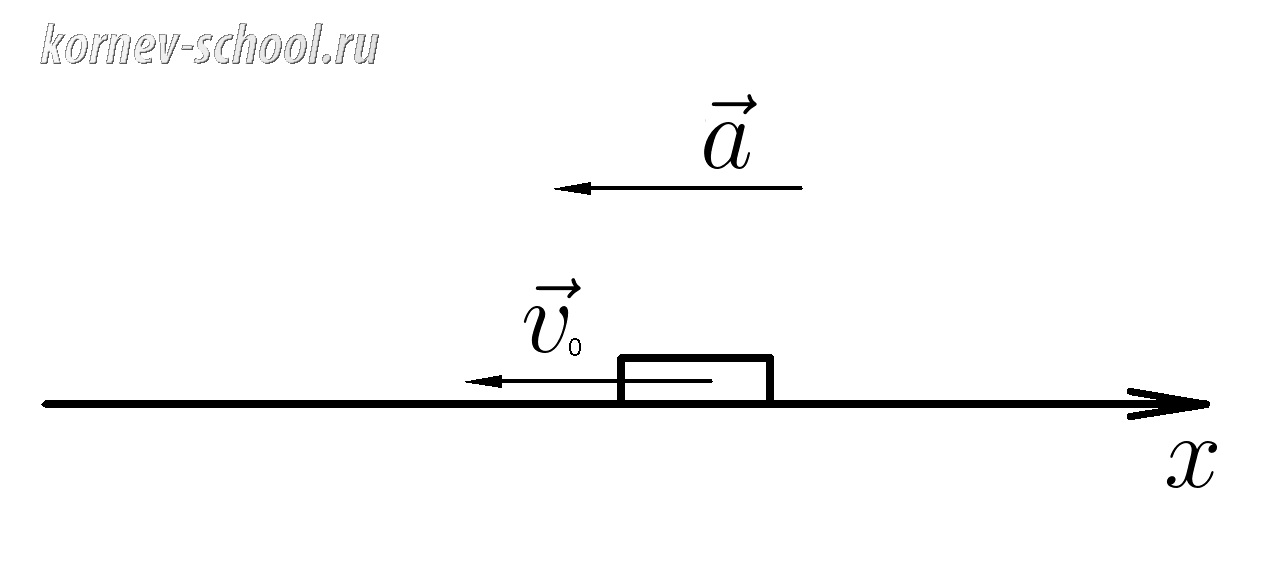
Дано:
\(a_x = -0,5 \;м/с^2 \)
\(v_{0x}=-15 \;м/с \)
\(t=10с \)
\(v_x-?\)
\(v_x=v_{0x}+a_xt \)
\(v_x=-15\;м/с- 0,5 \;м/с^2 \cdot 10с = -20\;м/с \)
Ответ: \(v_x=-20\;м/с \)
17. Вектор начальной скорости тела направлен против положительного направления оси абсцисс.
Вектор ускорения сонаправлен с ним.Проекция начальной скорости тела \(v_{0x}= -15м/с \) , проекция ускорения равна \(a_x=-0,5м/с^2 \). Найти модуль скорости через 10 секунд.
Показать ответ
Показать решение
Видеорешение
Если вектор начальной скорости и вектор ускорения сонаправлены и направлены против положительного направления оси,то модуль скорости тела будет возрастать,а проекция скорости будет убывать
Дано:
\(a_x = -0,5 \;м/с^2 \)
\(v_{0x}=-15 \;м/с \)
\(t=10с \)
\(|v|-?\)
\(|v|=|v_{0x}+a_xt| \)
\(|v|=|-15\;м/с- 0,5 \;м/с^2 \cdot 10с| = 20\;м/с \)
Ответ: \(|v|=20\;м/с \)
Задачи на кинематику(найти время) .
18. За какое время мотоциклист, двигаясь с ускорением \(0,5 м/с^2 \),
увеличит свою скорость с 12 до 28 м/с?
Показать ответ
Показать решение
Видеорешение
\( a=\dfrac{v-v_0}{t} \)
Умножим обе части первого уравнения кинематики на время:
\( a\cdot t=\dfrac{v-v_0}{t}\cdot t \)
\( a\cdot t=v-v_0 \)
Разделими обе части первого уравнения кинематики на ускорение:
\(\dfrac{a\cdot t}{a}=\dfrac{v-v_0}{a} \)
\( t=\dfrac{v-v_0}{a} \)
Дано:
\(a = 0,5 \;м/с^2 \)
\(v_0=12 \;м/с \)
\(v=28 \;м/с \)
\(t-?\)
\( t=\dfrac{v-v_0}{a} \)
\( t=\dfrac{28 \;м/с-12 \;м/с}{0,5 \;м/с^2}=32с \)
Ответ: \(t=32с \)
19. За какое время поезд, двигаясь с ускорением \(0,05 м/с^2 \),
увеличит свою скорость с 2 до 8 м/с?
Показать ответ
Показать решение
Видеорешение
\( a=\dfrac{v-v_0}{t} \)
Умножим обе части первого уравнения кинематики на время:
\( a\cdot t=\dfrac{v-v_0}{t}\cdot t \)
\( a\cdot t=v-v_0 \)
Разделими обе части первого уравнения кинематики на ускорение:
\(\dfrac{a\cdot t}{a}=\dfrac{v-v_0}{a} \)
\( t=\dfrac{v-v_0}{a} \)
Дано:
\(a = 0,05 \;м/с^2 \)
\(v_0=2 \;м/с \)
\(v=8 \;м/с \)
\(t-?\)
\( t=\dfrac{v-v_0}{a} \)
\( t=\dfrac{8 \;м/с-2 \;м/с}{0,05 \;м/с^2}=120с \)
Ответ: \(t=120с \)
20. За какое время поезд остановится, если проекция ускорения \(a=-2,5 м/с^2 \), а начальная скорость 10 м/с?
Показать ответ
Показать решение
Видеорешение
\( a=\dfrac{v-v_0}{t} \)
Умножим обе части первого уравнения кинематики на время:
\( a\cdot t=\dfrac{v-v_0}{t}\cdot t \)
\( a\cdot t=v-v_0 \)
Разделими обе части первого уравнения кинематики на ускорение:
\(\dfrac{a\cdot t}{a}=\dfrac{v-v_0}{a} \)
\( t=\dfrac{v-v_0}{a} \)
Дано:
\(a = -2,5 \;м/с^2 \)
\(v_0=10 \;м/с \)
\(v=0 \;м/с \)
\(t-?\)
\( t=\dfrac{v-v_0}{a} \)
\( t=\dfrac{0 \;м/с-10 \;м/с}{-2,5 \;м/с^2}=4с \)
Ответ: \(t=4с \)
21. Мототком бьют по гвоздю,модуль ускорения при торможении молотка равен \(\;\;100 м/с^2 \), а начальная скорость \( 20 м/с \). Сколько времени длится удар?
Показать ответ
Показать решение
Видеорешение
При торможении вектор начальной скорости и вектор ускорения разнонаправлены и если проекция скорости
положительна, то проекция ускорения отрицательна
Дано:
\(a = -100 \;м/с^2 \)
\(v_0=20 \;м/с \)
\(v=0 \;м/с \)
\(t-?\)
\( t=\dfrac{v-v_0}{a} \)
\( t=\dfrac{0 \;м/с-20 \;м/с}{-100 \;м/с^2}=0,2с \)
Ответ: \(t=0,2с \)
22. Поезд через \(10 с\) после начала движения приобретает скорость \(\;\;0,6 м/с \). Через сколько времени от начала движения скорость поезда станет равна \( 3м/с \)?
Показать ответ
Показать решение
Видеорешение
Каждый выбирает для себя то решение, которое ему понятнее
Решение номер 1 (для тех, кому тяжело вникнуть)
Читаем:"Поезд через 10 с после начала движения приобретает скорость 0,6 м/с"
Дальше не читаем, из этих данных находим ускорение
Дано:
\(t_1 = 10 \;с \)
\(v_0=0 \;м/с \)
\(v_1=0,6 \;м/с \)
\(v_2=3м/с \)
\(t_2-?\)
\(a=\dfrac{v_1-v_0}{t_1} \)
\(a=\dfrac{0,6м/с-0м/с}{10c}=0,06м/с^2 \)
а теперь решим задачу:
За какое время поезд разгонится до \( 3м/с \), двигаясь с ускорением \(0,06м/с^2\)
\(t_2=\dfrac{v_2-v_0}{a} \)
\(t_2=\dfrac{3м/с-0м/с}{0,06м/с^2}=50с \)
Ответ: \(t_2=50с \)
Решение номер 2
Дано:
\(t_1 = 10 \;с \)
\(v_1=0,6 \;м/с \)
\(v_2=3м/с \)
\(v-?\)
\(a=\dfrac{v_1-v_0}{t_1} \;\;\;\;\;\;\;\;\;\;t_2=\dfrac{v_2-v_0}{a} \)
Так как \(v_0=0:\)
\(a=\dfrac{v_1}{t_1} \;\;\;\;\;\;\;\;\;\;t_2=\dfrac{v_2}{a} \)
\( t_2=\dfrac{\;\;\;\;\;\;v_2\;\;\;\;\;\;}{(\dfrac{v_1}{t_1})}=
\dfrac{v_2}{1}:\dfrac{v_1}{t_1}=\dfrac{v_2}{1}\cdot\dfrac{t_1}{v_1}=\dfrac{v_2t_1}{v_1}= \dfrac{3м/с\cdot10с}{0,6 \;м/с}=50с\)
Ответ: \(t_2=50с \)