Тренировочный вариант ЕГЭ №1.
Задание 1.
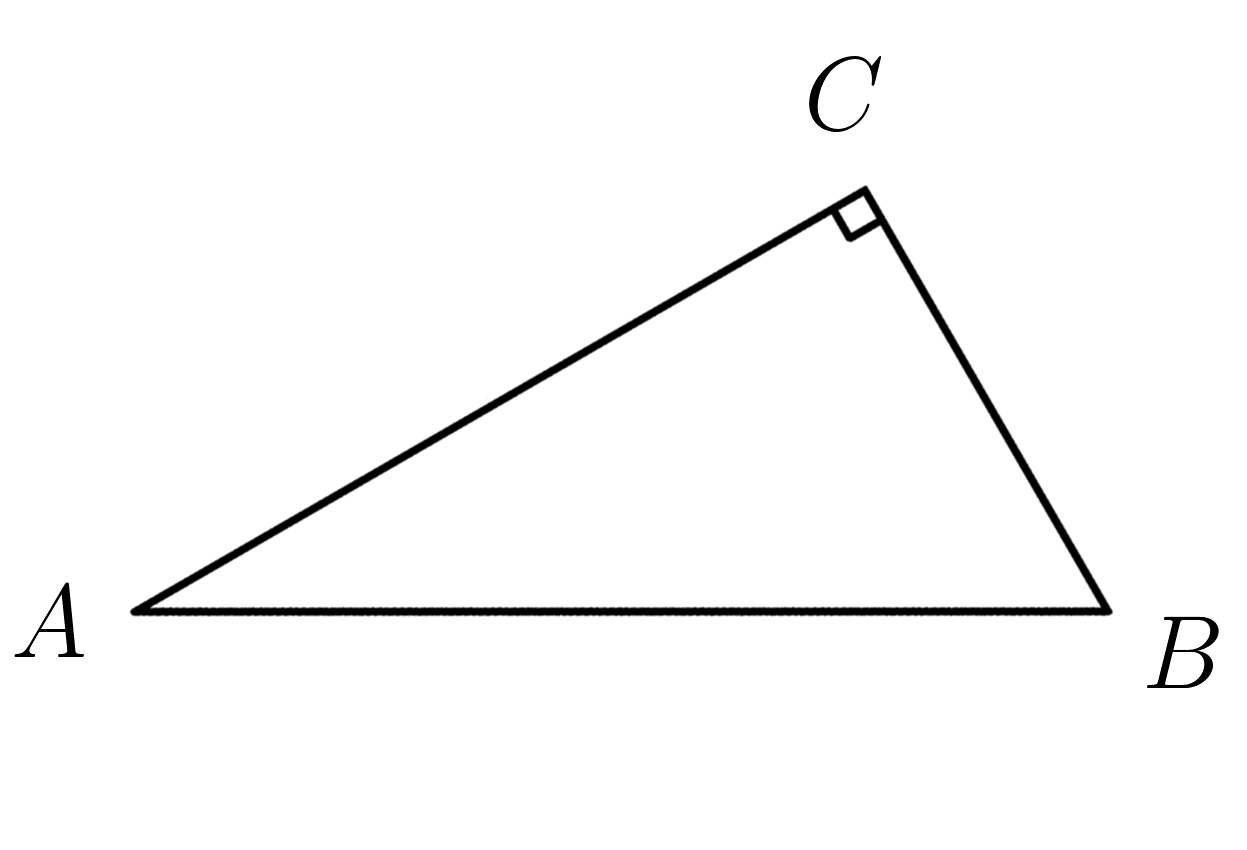
Гипотенуза \(AB=\sqrt{60} , \; cos\:A = \dfrac{\sqrt{11}}{\sqrt{60}}\). Найти катет \(CB\)
Задание 2.
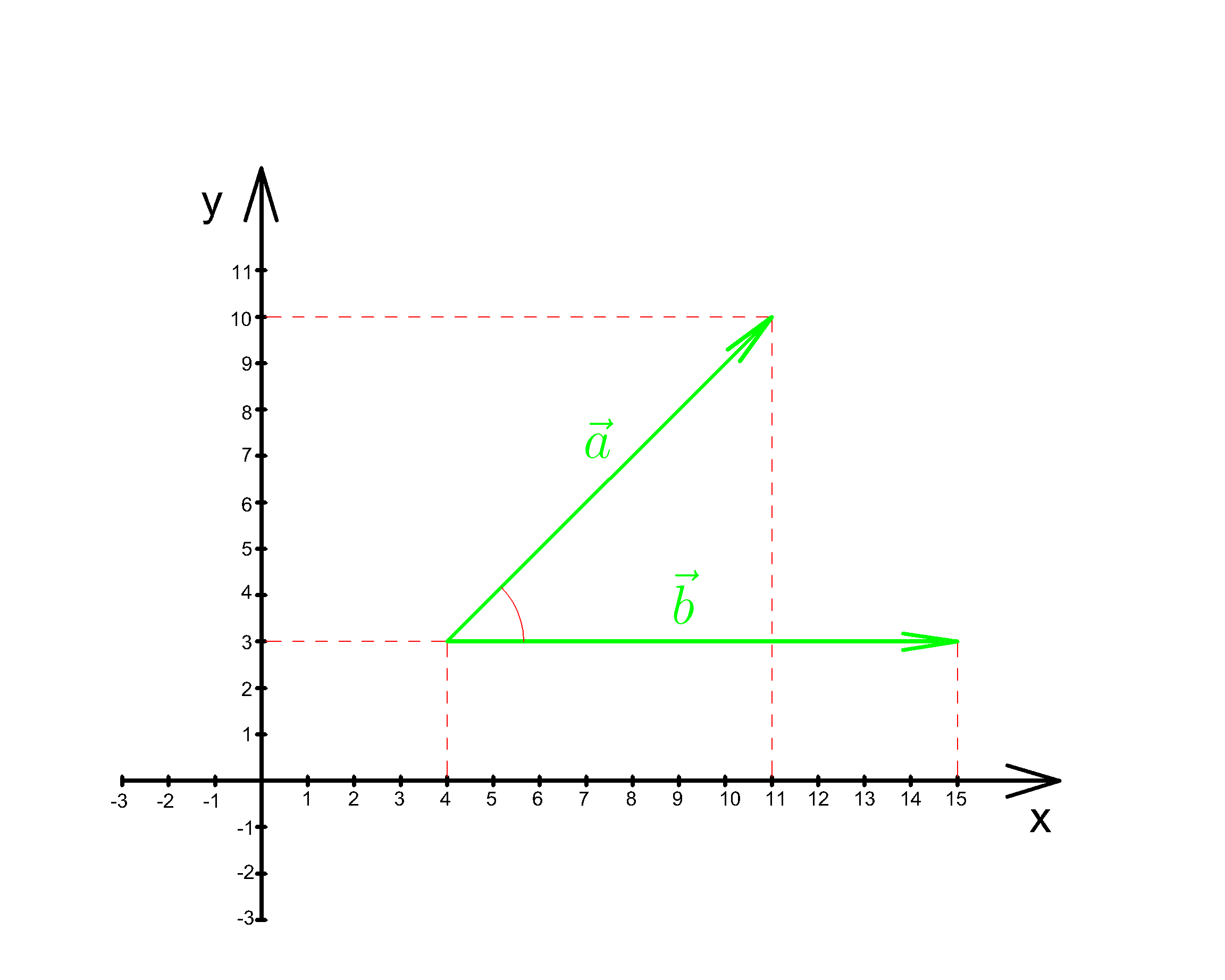
Найти угол между векторами \(\vec{a} \) и \(\vec{b} \)
Задание 3.
В вертикальном цилиндрическом резервуаре хранится нефть, высота уровня ее достигает \( H_{1}=45 \ см \) . Нефть перекачивают в вертикальную цистерну также имеющую форму цилиндра. Радиус резервуара в 2 раза больше радиуса цистерны. Какой будет высота уровня нефти в цистерне? Дать ответ в метрах.
Задание 4.
На каждые 710 полностью исправных автомобилей, выпускаемых автозаводом, приходится 90 машин, которые имеют хотя бы одну неисправность. Какова вероятность приобрести автомобиль, имеющий неисправность?
Задание 5.
Двое друзей собираются играть в пейнтбол, всего у них два комплекта снаряжения. Каждый комплект представляет из себя пневматическое ружье и воздушный баллон высокого давления. Для игры нужно чтобы ни один элемент не вышел из строя. Вероятность выхода из строя баллона равна 0,2. Вероятность выхода из строя ружья равна 0,1. Какова вероятность что игра состоится?
Задание 6.
\( 6x^2-18x =0 \)
В ответе запишите сумму корней этого уравнения
Задание 7.
Найти значение выражения:
\( \dfrac{14^{n+3} }{7^{n+2}\cdot 2^{n-3}} \)
Задание 8.
Прямая \(y=6x-5\) является касательной к графику \(f(x)=x^3+2x^2-x+d\). .
Найти \(d\) , если абсцисса точки касания положительна.
Задание 9.
Решите уравнение:
\( y^2 -y-6=0 \)
В ответе записать корни в порядке возрастания без пробелов,
например если получены корни 1 и 1,5, то нужно вписать 11,5
Задание 10.
В бочку залили 1 кг незамерзающей жидкости с концентрацией изопропилового спирта в 40% и 3 кг незамерзающей жидкости с концентрацией изопропилового спирта в 20%. Какова итоговая концентрация спирта в бочке?
Задание 11.
На рисунке представлен график функции \(y=ax^2+bx+c . \)
Вычислите \(f(20) \)

Задание 12.
Найдите точку минимума функции:
\( f(x)=\dfrac{2 \sqrt{x^3}}{3}-3x+ \dfrac{1}{17} \)