Тренировочный вариант ЕГЭ №2.
Задание 1.
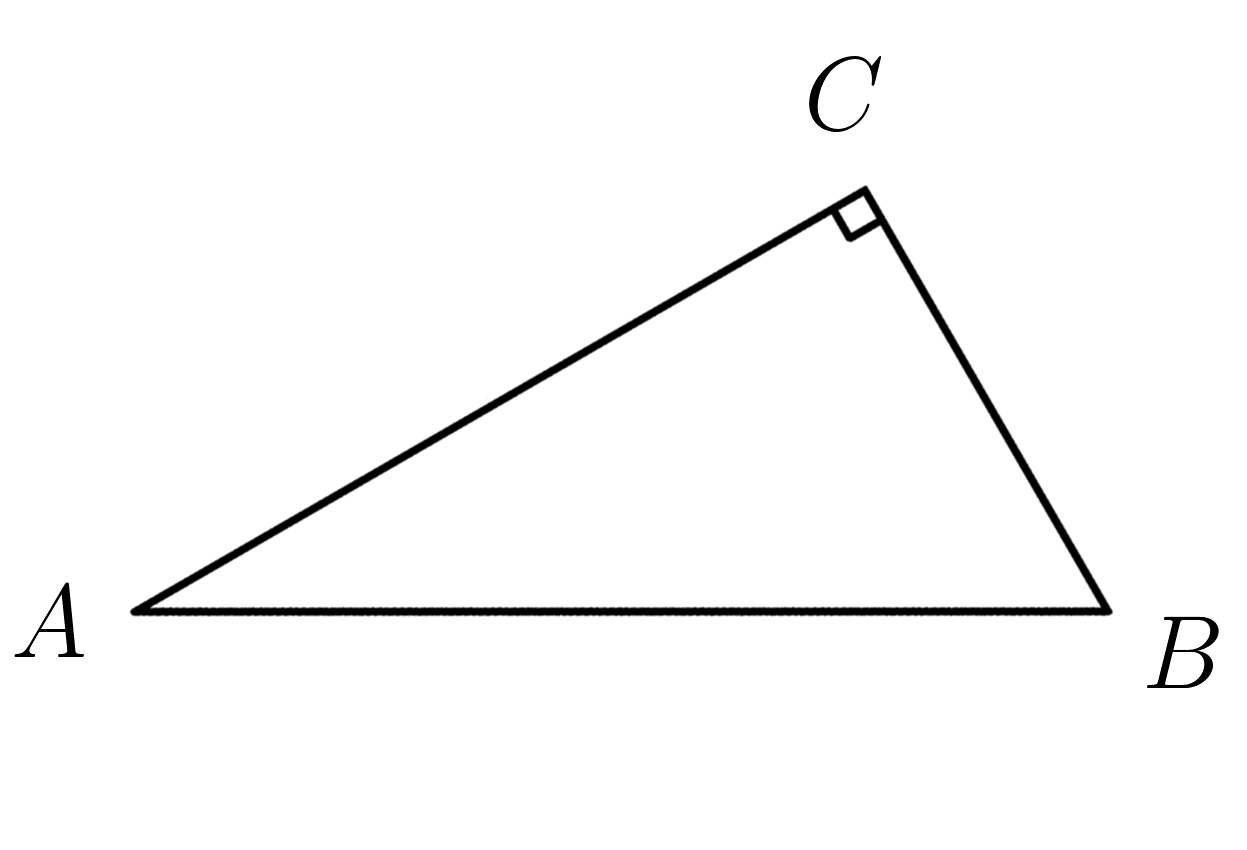
Угол \(C=90^0 \) . Гипотенуза \(AB=10; AC=8 . \; Найти \ длину \ медианы \ CK\)
Задание 2.
Найти скалярное произведение векторов \(\vec{a}=(1;0,5) \) и \(\vec{b}=(0,4;0,4) \)
Задание 3.
В правильной четырехугольной пирамиде сторона основания равна 6, а высота 4. Вычислите ее объем.
Задание 4.
Бросают два игральных кубика. Вычислите вероятность того, что произведение выпавших очков будет равняться шести? Округлите ответ до сотых.
Задание 5.
Два лучника стреляют в яблоко, вероятность, что попадет первый 0,25. Вероятность, что попадет второй 0,4. Вычислите вероятность того, что один из них попадет, а другой промахнется.
Задание 6.
\( 2^{x+1}+2^{x-1}=10 \)
Задание 7.
Найти значение выражения:
\( \dfrac{(3x)^4 \cdot x^{-10}}{x^{-9}\cdot 5x^4} \) при \(x=2\)
Задание 8.
Вычислите значение производной функции:
\( y(x)=3x^2-ln \ x \)
в точке \(x=1\)
Задание 9.
Под каким углом к горизонту был выпущен снаряд из ствола артиллерийского орудия, если дальность полета этого снаряда составила 49000 метров, начальная скорость снаряда \(v_0=700 \ м/с . \), а ускорение свободного падения \(g=10м/с^2 . \) Формула для нахождения дальности полета тела, брошенного под углом к горизонту:
\(l= \dfrac{v_{0}^2 \cdot sin \; 2\alpha }{g} \)
Задание 10.
Расстояние между причалом А и причалом В по реке составляет 105 километров. С этих причалов навстречу друг другу стартуют два катера, с одинаковой собственной скоростью, один катер идет по течению, а другой против. Встреча катеров происходит через 2 часа с момента старта. Чему равна собственная скорость катера?
Задание 11.
На рисунке представлен график функции \(y=ax^2+bx+c . \)
Вычислите \(f(-20) \)

Задание 12.
Найдите точку минимума функции:
\( f(x)=\dfrac{2 \sqrt{x^3}}{3}-3x+ \dfrac{1}{17} \)