Тренировочный вариант ЕГЭ №4.
Задание 1.
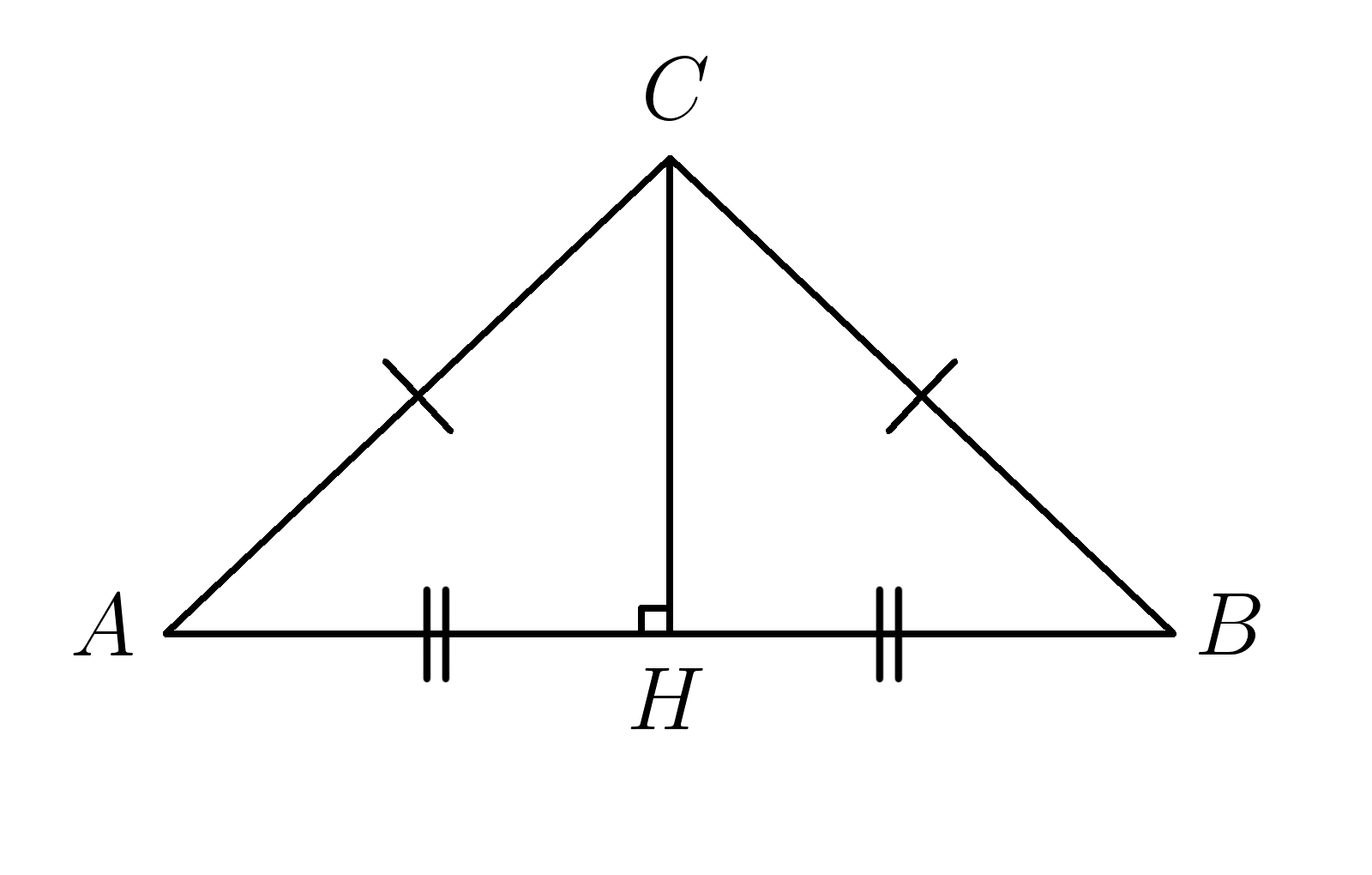
Треугольник \(ABC \) равнобедренный\( (AC=BC) \) . \( sin\;B=\dfrac{5}{\sqrt{34}}\;, \;\;CH=45 \) . Найти \(AB \)
Задание 2.
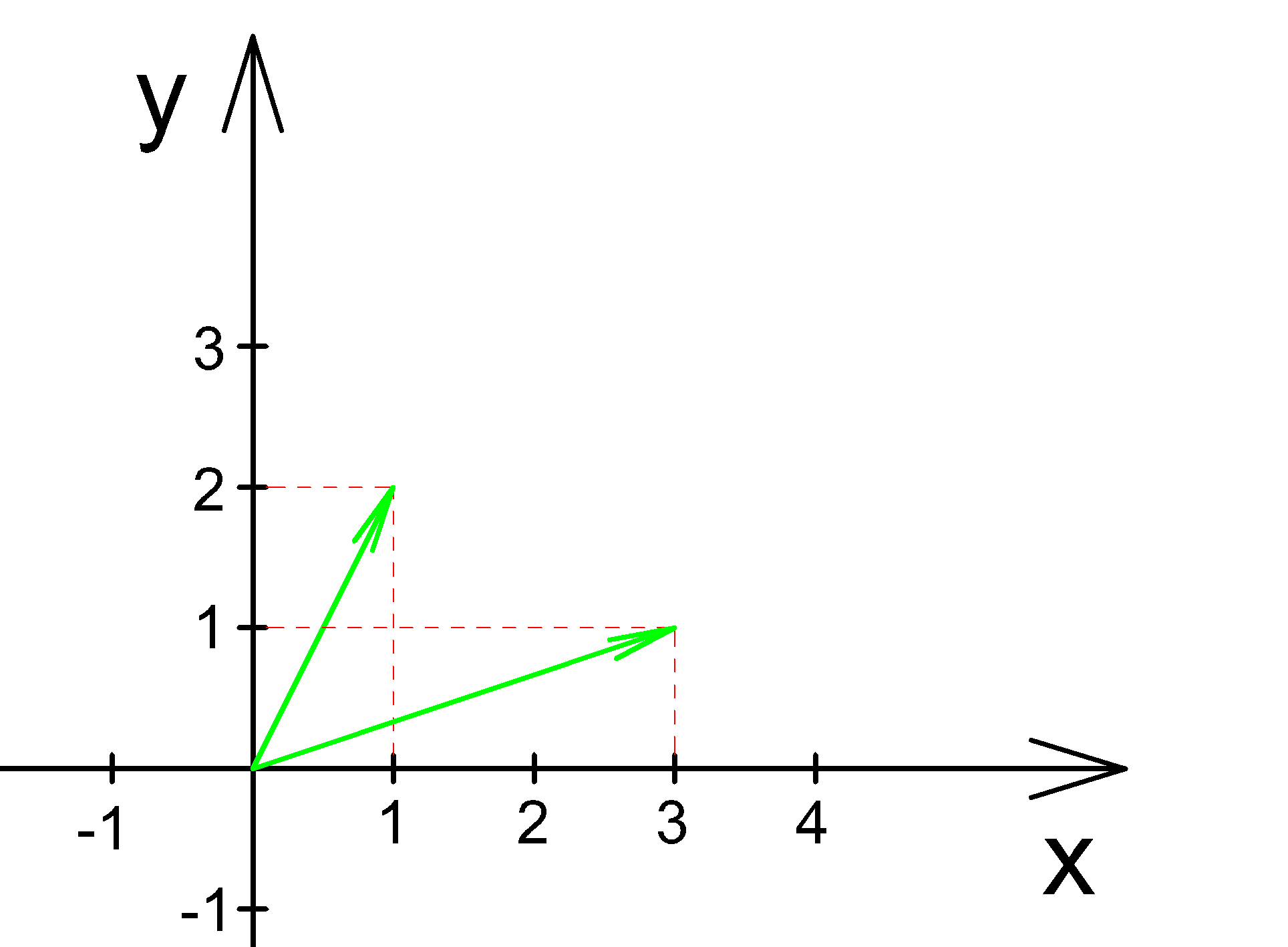
Найти угол между векторами изображенными на рисунке
Задание 3.
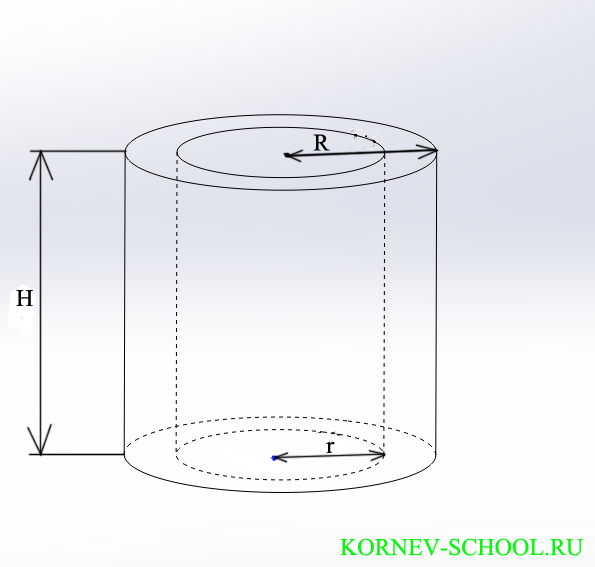
Вычислите объем фигуры, изображенной на рисунке .
\(H=9 \)
\(R=\dfrac{7}{ \sqrt {\pi} } \)
\(r=\dfrac{4}{ \sqrt {\pi} } \)
Задание 4.
На телефон Николая на каждые 100 входящих звонков от родственников, знакомых или друзей приходится 25 входящих звонков от телефонных мошенников или рекламных ботов. В какой-то момент у Николая звонит телефон. Какова вероятность, что это звонят телефонные мошенники или рекламные боты?
Задание 5.
Гаубица поражает неподвижную цель с вероятностью 0,2 при первом выстреле. Всего имеется 8 снарядов. При каждом последующем выстреле вероятность поражения увеличивается на 0,1. Какое минимальное количество выстрелов необходимо произвести, чтобы вероятность поражения цели составила не менее 0,9 ?
Задание 6.
\( \left ( \dfrac{1}{9} \right )^{x+13}=27 \)
Задание 7.
\(sin \: \alpha= \dfrac{1}{2} \; . \;\;\;\; \) Найти \(5\sqrt{3}tg \: \alpha \) .\(\;\;\;\;( \ 90^0<\alpha<180^0) .\)
Задание 8.
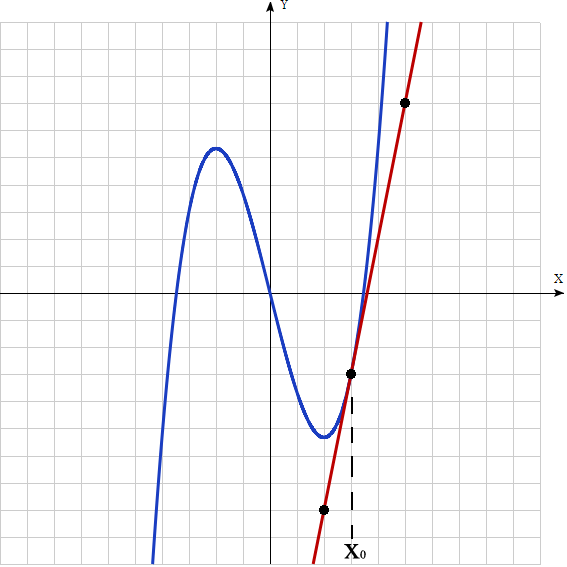
На рисунке показан график функции \( f(x) \) и касательная к нему в точке \(x_0 \)
Найдите значение производной функции в точке \(x_0 \)
Задание 9.
Какова сила тока \(I\) в кипятильнике, включенном в сеть с напряжением \(U=220 \ В \), если воду массой \(m_{в}=2 \ кг \), находящуюся в алюминиевой кастрюле массой \(m_{к}=1 \ кг \) он может довести до кипения за время \( \tau= 800 \ секунд ? \) Начальная температура воды \(t_1=12 ^0 \ C . \)
КПД кипятильника \( \eta=50 \ \% .\)
Удельная теплоемкость воды \(c_в=4200\dfrac{Дж}{кг\cdot ^0C} .\)
Удельная теплоемкость алюминия \(c_а=920\dfrac{Дж}{кг\cdot ^0C} .\)
КПД данного процесса можно рассчитать по формуле:
\( \eta=\dfrac{c_вm_в(t_2-t_1)+c_аm_к(t_2-t_1)}{IU \tau} \)
Задание 10.
Гидроцикл проплыл по течению реки 30 км, после чего повернул назад и вернулся в исходную точку. Известно, что путь обратно занял на 6 минут больше времени чем путь туда. Найдите собственную скорость гидроцикла, если скорость течения 5 км/ч.
Задание 11.
На рисунке представлены две параболы, которые пересекаются в точке A(1;1) и точке B.
Найдите ординату точки B

Задание 12.
Найдите точку минимума функции:
\( f(x)=x^3+5x^2+7x-\dfrac{5}{441} \)