Тренировочный вариант ОГЭ №2.
Задание 1.
Человек планирует воспользоваться услугой грузовых перевозок для доставки строительных материалов на дачу.
Планируется перевезти доски длиной 6 метров, по правилам дорожного движения груз не дожен выступать более чем на 2 метра за пределы габаритов автомобиля.
| № автомобиля | Автомобиль | Длина борта, м |
|---|---|---|
| 1 | Соболь | 2,9 |
| 2 | Газель | 5 |
| 3 | Хендай HD78 | 5,8 |
Задание 2.
Человек планирует воспользоваться услугой грузовых перевозок для доставки строительных материалов на дачу.
Планируется перевезти утеплитель в грузовом фургоне, фургон имеет длину 2,5 метра, ширину 1,5 метра и высоту 1,5 метра. Найти объем фургона в кубических метрах.
Задание 3.
Какой диаметр у колеса размерностью 185/70 R14 ?
Задание 4.
Какое расстояние проедет автомобиль с колесами размерностью 185/70 R14 , за 1 оборот колеса?
\( \pi=3,14 . \) Ответ дать в миллиметрах. В ответе записать точное число без округления.
Задание 5.
Какое расстояние проедет автомобиль с колесами размерностью 185/70 R14 , если каждое его колесо совершит 250000 оборотов?
\( \pi=3,14 . \) Ответ дать в метрах.
Задание 6.
Вычислите:
\( \dfrac{13}{10} \cdot \left( \dfrac{5}{13}+\dfrac{4}{5}:\dfrac{2}{3} \right ) \)
Задание 7.
На координатной прямой отмечено число \(m\). Выберите верное утверждение:
В ответе запишите номер верного утверждения.

\( 1) \ m<-5 \)
\( 2) \ -2 \cdot m<-10 \)
\( 3) \ -3 \cdot m>12 \)
\( 4) \ \ 2m+10>4 \)
Задание 8.
Упростите выражение:
\( (1+\dfrac{1}{a}):(1-\dfrac{1}{a}) \)
и вычислите его значение при \(a=9 \)
Задание 9.
Решите уравнение:
\( y^2 -y-6=0 \)
В ответе записать корни в порядке возрастания без пробелов,
например если получены корни 1 и 1,5, то нужно вписать 11,5
Задание 10.
На каждые 710 полностью исправных автомобилей, выпускаемых автозаводом, приходится 90 машин, которые имеют хотя бы одну неисправность. Какова вероятность приобрести автомобиль, имеющий неисправность?
Задание 11.
На рисунке представлен график функции \(y=ax^2+bx+c . \)
Пользуясь графиком, найдите коэффициент \( a . \)

Задание 12.
Уравнение Менделеева-Клапейрона имеет вид:
\( PV=\nu RT \)
Давление \(P= 8,31 \cdot 10^6 \; Па . \) Количество вещества газа \( \nu=100 \ Моль . \)
Универсальная газовая постоянная \( R=8,31 \frac{Дж}{Моль \cdot K} . \)
Температура газа \(T=300 К .\)
Найдите объем \( V . \)
Задание 13.
Какой из интервалов удовлетворяет решению данного неравенства
\( x^2+12x+20 \leq 0 \)
\( 1) \ \ (-10;-2) \)
\( 2) \ \ (-\infty;-10] \bigcup [-2;+ \infty) \)
\( 3) \ \ (-\infty;-10) \bigcup (-2;+ \infty) \)
\( 4) \ \ [-10;-2] \)
\( 5) \ \ (-\infty;6) \bigcup (7;+ \infty) \)
\( 6) \ \ (-\infty;6] \bigcup [7;+ \infty) \)
В ответе запишите номер варианта
Задание 14.
Имеется 7 различных конфигураций старых компьютеров, известно что объем оперативной памяти у каждой следующей конфигурации в k раз больше, чем у предыдущей. k - целое число. У компьютера третьей конфигурации объем оперативной памяти составляет 32 мегабайт. У компьютера пятой конфигурации объем оперативной памяти составляет 512 мегабайт. Какой объем оперативной памяти у компьютера седьмой конфигурации? Дать ответ в мегабайтах.
Задание 15.
В треугольнике \(KMP\) проведена медиана \(ME\) и высота \(MB\).
\( ME=MP . \) Вычислите длину основания \(KP\), если \(KB=264 . \)
Задание 16.

\( \angle AOB =99^0, \;\; OA \) является биссектрисой угла \( CAB. \)
Вычислите \( \angle BOC \) .
Задание 17.

Площадь трапеции, изображенной на рисунке равна 5000, при этом \(BH=40 \) , а верхнее основание равно 50.
Вычислите длину нижнего основание.
Задание 18.
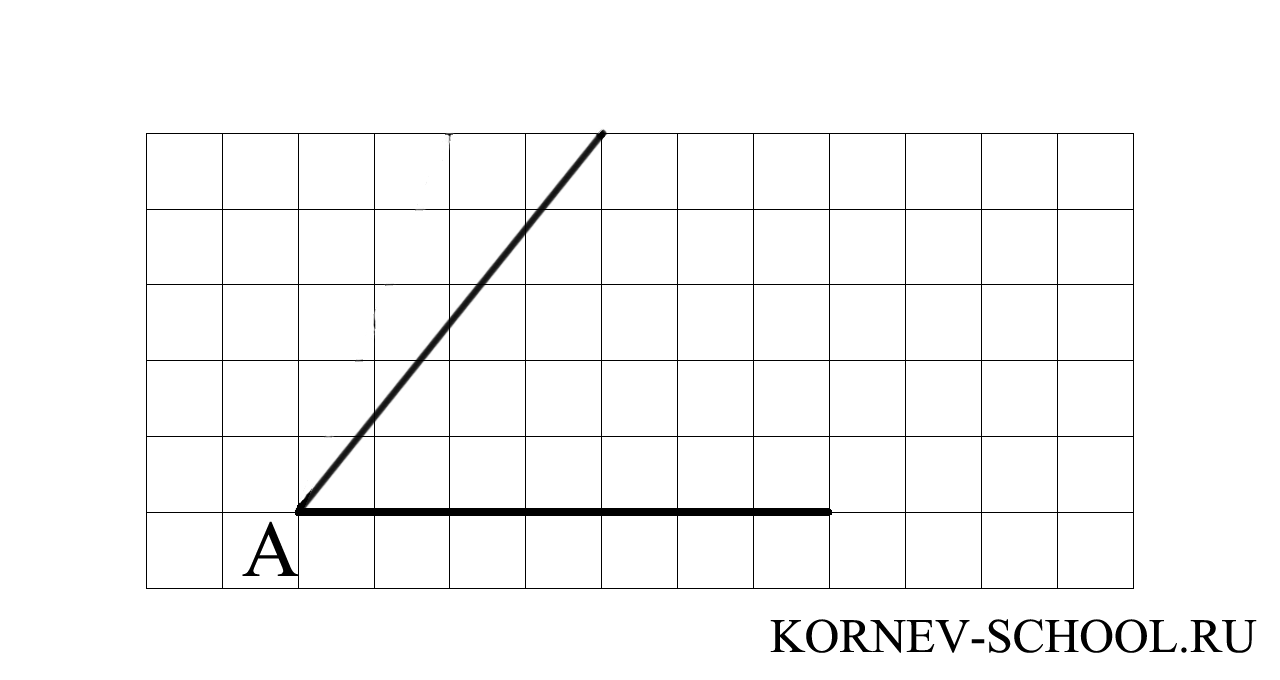
Определите по рисунку значение тангенса угла \( A \)
Задание 19.
Укажите номера верных утверждений:
1) Если треугольники подобны то они равновеликие
2) Смежные углы могут быть не равны друг другу
3) Вертикальные углы могут быть не равны друг другу
Задание 20.
Найдите значение выражения:
\( \left( \sqrt{ (3\sqrt{7}-4\sqrt{6})^2}+3\sqrt{7} \right ) \cdot\sqrt{54} \)
Задание 21.
В бочку залили 1 кг незамерзающей жидкости с концентрацией изопропилового спирта в 40% и 3 кг незамерзающей жидкости с концентрацией изопропилового спирта в 20%. Какова итоговая концентрация спирта в бочке?
Задание 22.
Постройте график функции:
\(y= \dfrac{x^4+5x^2-36}{x^2-4} \)
и определите при каком значении параметра \(a \) большем чем 9 ( \( a>9 \) )
прямая \( y=a \) не имеет общих точек с этим графиком
В ответе записать значение параметра \(a \)
Задание 23.
Острый угол ромба равен 30 градусов, а его сторона равна 15, вычислите длину перпендикуляра, проведенного из точки пересечения диагоналей ромба к его стороне.
Задание 25.
В параллелограмме \(ABCD\) одна сторона в 2 раза больше другой. Проведены биссектрисы углов \(A\) и \(B\). Эти биссектрисы пересекают прямую, содержащую сторону \(CD\) в точках \(L\) и \(M\) . Длина отрезка \( LM \) равна \( 7\sqrt{11} \), а косинус одного из углов параллелограмма равен \( \dfrac{\sqrt{19}}{10} \) . Найти площадь параллелограмма.