Преломление света.Закон Снеллиуса
Репетитор по физике
8 916 478 10 32
При переходе из одной среды в другую луч преломляется(отклоняется от начального направления), это обусловлено разной скоростью света в двух средах.
Самая большая скорость света в вакууме и в воздухе.
\(n \) это показатель преломления
для воздуха и вакуума \(n=1 \)
для стекла \(n=1,5 \)
Рассмотрим пример перехода луча из воздуха в стекло:
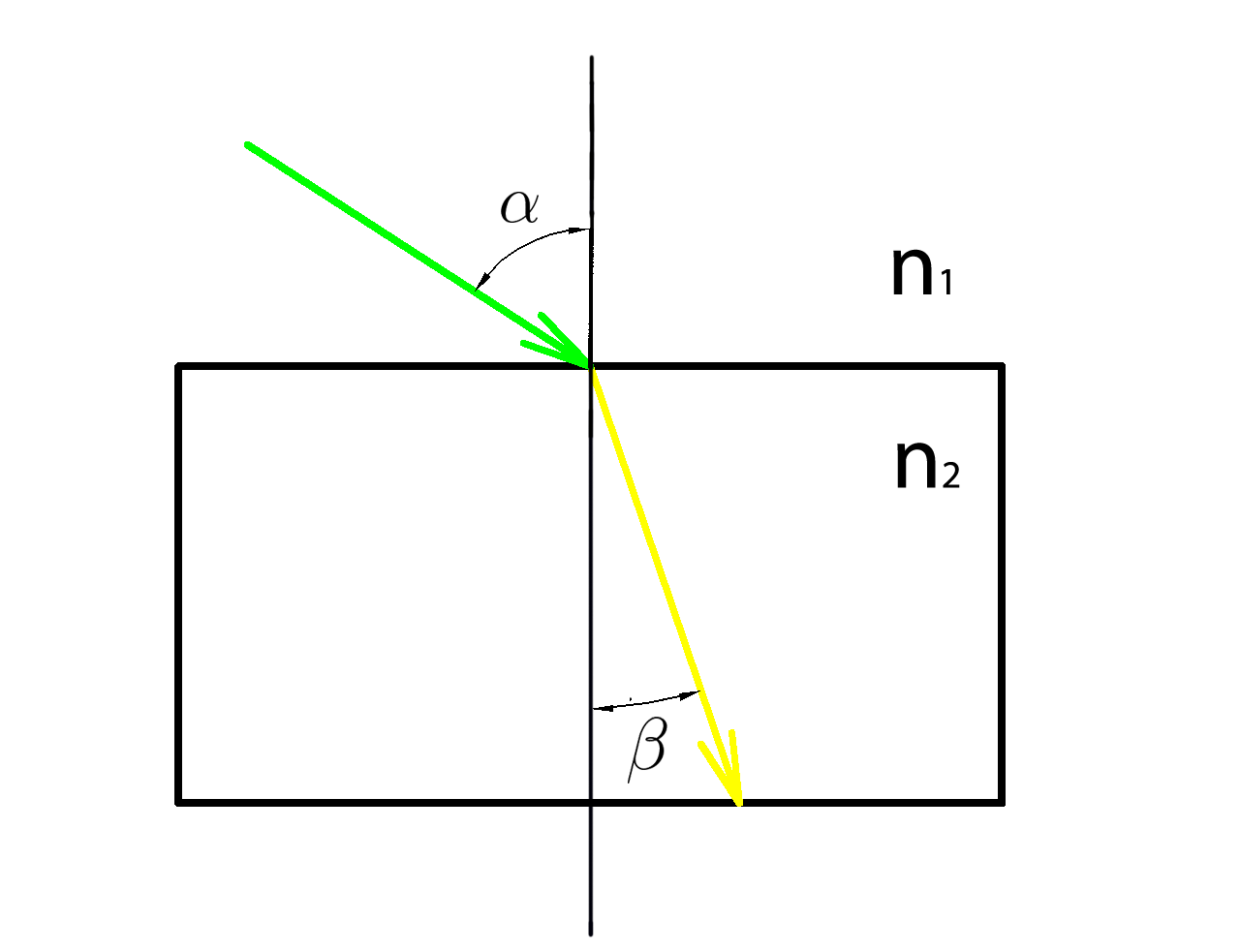
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{n_1}\)
\(n_1=1 \) показатель преломления воздуха
\(n_2=1,5 \) показатель преломления стекла
Угол падения \(\alpha \) отсчитывается от вертикали
Угол преломления \( \beta \) отсчитывается от вертикали
Задача 1. (Преломление света.Закон Снеллиуса)
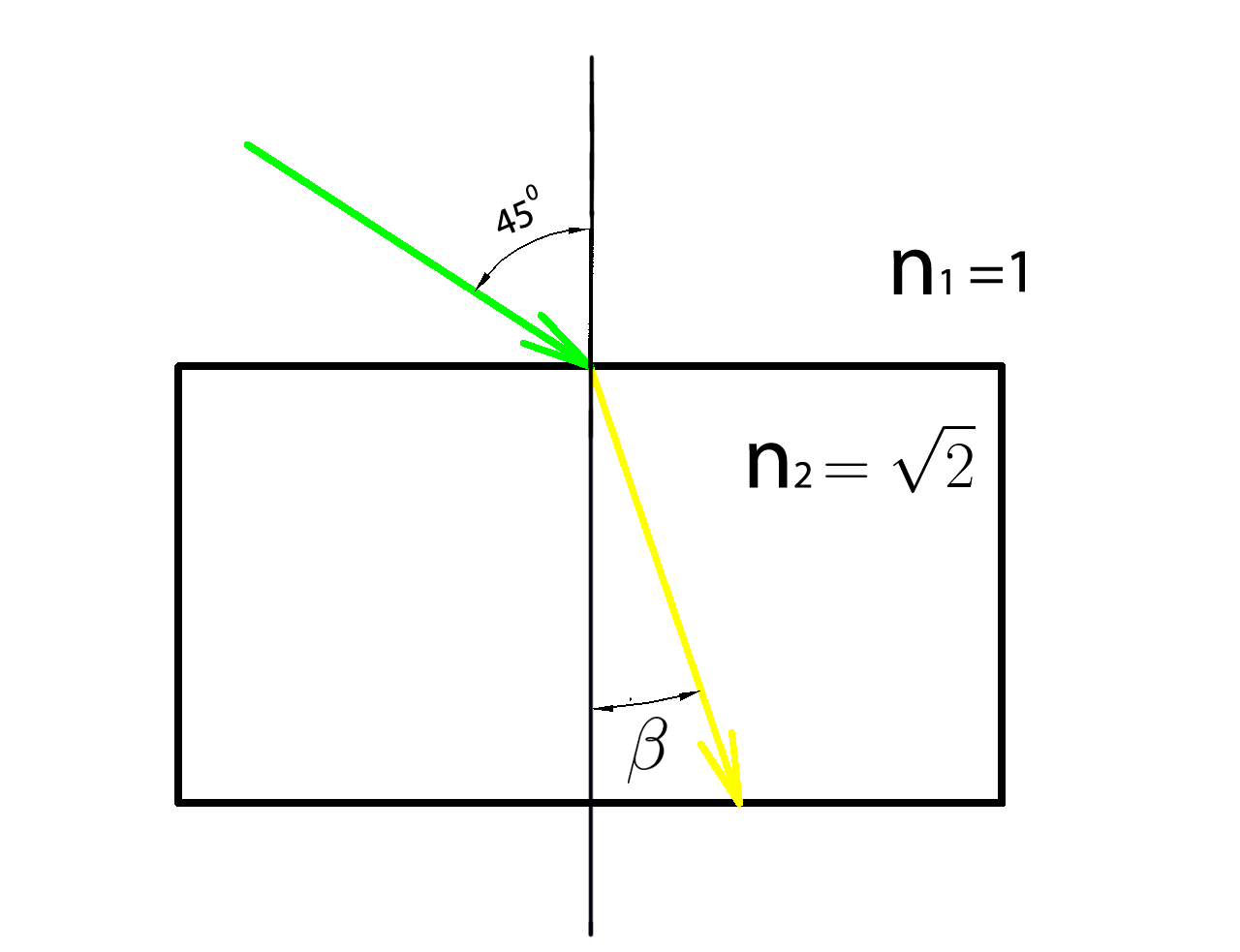
Луч света падает из воздуха на плоскую горизонтальную прозрачную поверхность под углом \( \alpha=45^0 . \)
Показатель преломления материала среды этой поверхности равен \(\sqrt{2} . \)
Найдите угол преломления луча \( \beta . \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( \alpha=45^0 \)
\( n_2=\sqrt{2} \)
\(\beta-?\)
Запишем закон Снеллиуса:
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{n_1}\)
Просто вставим числа:
\( \dfrac{sin \ 45^0 }{sin \ \beta}= \dfrac{\sqrt{2} }{1}\)
\( \dfrac{sin \ 45^0 }{sin \ \beta}= \sqrt{2} \)
\( sin \ 45^0 =\sqrt{2}sin \ \beta \)
\( \dfrac{\sqrt{2}}{2}=\sqrt{2}sin \ \beta \)
\( \dfrac{1}{2}=sin \ \beta \)
\( sin \ \beta=\dfrac{1}{2} \)
Синус какого угла равен \( \dfrac{1}{2} ? \)
\(\beta=30^0 \)
Ответ: \( \beta=30^0 \)
ПОЗЖЕ
Задача 2. (Преломление света.Закон Снеллиуса)
Луч света падает из воздуха на водную гладь под углом \( \alpha=30^0 \)
и преломляется с углом преломления \( \beta \) при переходе из воздуха в воду.
Показатель преломления воды \(n_2=1,33 . \)
Найдите синус угла преломления
Ответ округлить до тысячных.

Показать ответ
Показать решение
Видеорешение
Ответ: \( sin \ \beta =0,376 \)
Дано:
\( \alpha=30^0 \)
\( n_2=1,33 \)
\(sin \ \beta-?\)
Запишем закон Снеллиуса:
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{n_1}\)
Просто вставим числа:
\( \dfrac{sin \ 30^0 }{sin \ \beta}= \dfrac{1,33 }{1}\)
\( \dfrac{0,5 }{sin \ \beta}= 1,33 \)
\(0,5= 1,33 \cdot sin \ \beta \)
\( sin \ \beta= \dfrac{0,5}{1,33} \)
\( sin \ \beta \approx 0,3759\approx 0,376 \)
Ответ: \( sin \ \beta =0,376 \)
ПОЗЖЕ
Задача 3. (Преломление света.Закон Снеллиуса)
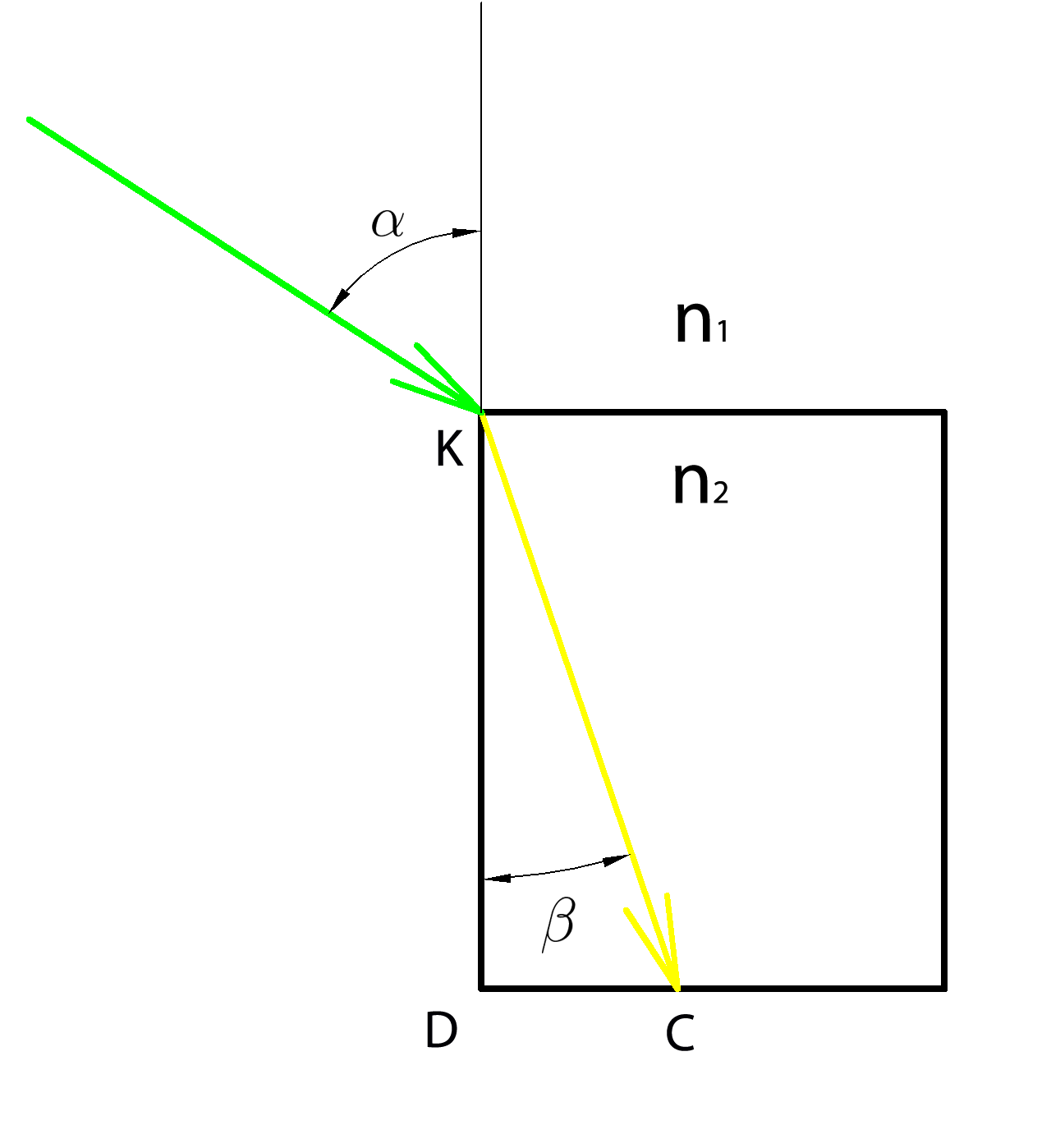
Луч света падает под углом \( \alpha=60^0 \) из воздуха в открытую тонкостенную емкость со сжиженым газом и
с высотой \( KD= 0,39 \ м . \)
Емкость имеет форму прямоугольного параллелепипеда.
Найдите расстояние \(DC \), на которое сместится преломленный луч от левой грани емкости .
Показатель преломления этого сжиженного газа \(n_2=\sqrt{\dfrac{3}{2}} . \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( \alpha=60^0 \)
\( n_2=\sqrt{\dfrac{3}{2}} \)
\( n_1=1 \)
\(DC-?\)
Запишем закон Снеллиуса:
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{n_1}\)
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{1}\)
\( \dfrac{sin \ \alpha }{sin \ \beta}= n_2 \)
\( {sin \ \beta}= \dfrac{sin \ \alpha }{n_2} \)
\( {sin \ \beta}= \dfrac{sin \ 60^0 }{\sqrt{\dfrac{3}{2}}} = \dfrac{\left(\dfrac{\sqrt{3}}{2} \right) }{\sqrt{\dfrac{3}{2}}}=
\dfrac{\sqrt{3}}{2}:\dfrac{\sqrt{3}}{\sqrt{2}} = \dfrac{\sqrt{3}} {2} \cdot \dfrac{\sqrt{2}} {\sqrt{3}} =\dfrac{\sqrt{2}} {2} \)
\( sin \ \beta= \dfrac{\sqrt{2}} {2} \)
\( \beta=45^0 \)
Это значит, что треугольник \(KDC \) равнобедренный.
\(DC=KD =0,39 \ м \)
Ответ: \( DC=0,39 \ м \)
ПОЗЖЕ
Задача 4. (Преломление света.Закон Снеллиуса)
Луч света падает под углом \( \alpha=45^0 \) из воздуха в вершину \( K \) стеклянного куба с ребром 400 миллиметров.
Найдите расстояние \(DC \), на которое сместится преломленный луч от левой грани куба.
Показатель преломления стекла \(n_2=1,5 . \)
Дать ответ в миллиметрах.
Ответ округлить до целого числа миллиметров.

Показать ответ
Показать решение
Видеорешение
Дано:
\( \alpha=45^0 \)
\( n_2=1,5 \)
\( n_1=1 \)
\( KD=400 \ мм \)
\(DC-?\)
Запишем закон Снеллиуса:
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{n_1}\)
\( \dfrac{sin \ \alpha }{sin \ \beta}= \dfrac{n_2}{1}\)
\( \dfrac{sin \ \alpha }{sin \ \beta}= n_2 \)
\( {sin \ \beta}= \dfrac{sin \ \alpha }{n_2} \)
\(ctg \ \beta= \dfrac{KD} {DC} \)
\(DC=\dfrac{KD} {ctg \ \beta} \)
Разделим основное тригонометрическое тождество на \( sin^2\;B \) :
\(sin^2 \;B+cos^2\;B=1\)
\( \dfrac{sin^2\;B}{sin^2\;B}+\dfrac{cos^2\;B}{sin^2\;B} = \dfrac{1}{sin^2\;B}\)
\(ctg^2 \;B+1=\dfrac{1}{sin^2\;B} \)
\(ctg^2 \;B=\dfrac{1}{sin^2\;B}-1 \)
\(ctg \ \beta=\sqrt { \dfrac{1}{sin^2 \ \beta}-1 } \)
\(DC=\dfrac{KD} {\sqrt { \dfrac{1}{sin^2 \ \beta}-1 }}= \dfrac{KD} {\sqrt { \dfrac{1}{\left( \dfrac{sin \ \alpha }{n_2} \right)^2}-1 }}\)
\(DC=\dfrac{KD} {\sqrt { \dfrac{n_{2}^2}{sin^2 \ \alpha }-1 }}\)
\(sin^2 \ \alpha= sin^2 \ 45^0= \left ( \dfrac{\sqrt{2}}{2} \right )^2=0,5 \)
\(DC=\dfrac{400} {\sqrt { \dfrac{1,5^2}{0,5 }-1 }} \approx 213,80899353 \approx 214 \ мм \)
Ответ: \( DC=214 \ мм \)
ПОЗЖЕ




