Расчет электрических схем

Репетитор по физике

Задача 1. ( Расчет электрических схем)
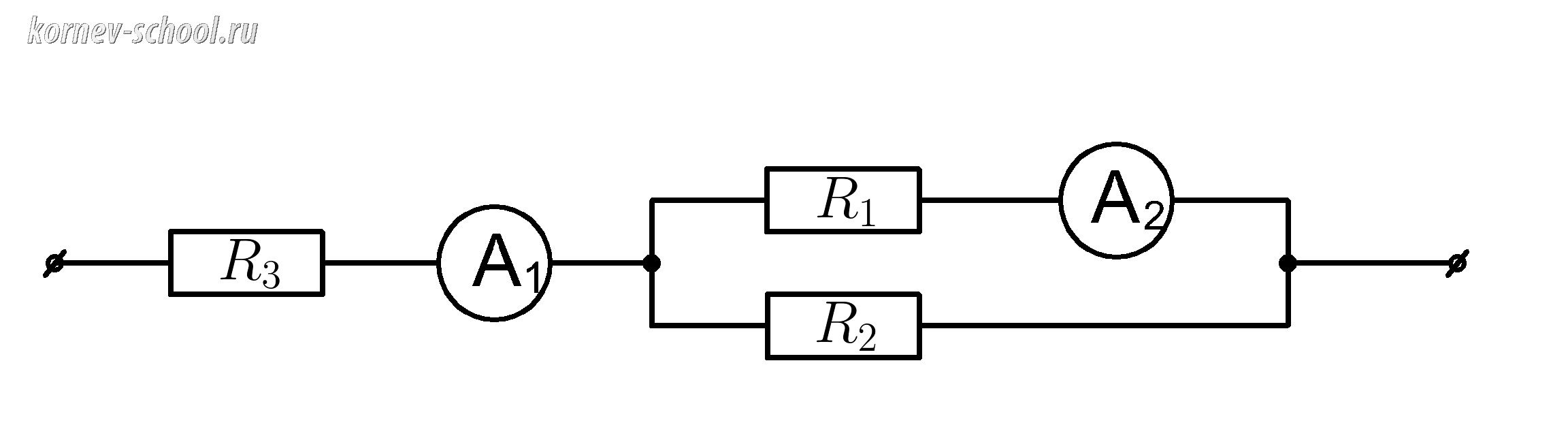
На схеме изображенной на рисунке амперметр \(A_1 \) показывает силу тока \(I=9 А \) , определить показания амперметра \(A_2 \) , если \(R_1=3 Ом \; , \; R_2=6 Ом , \; R_3=28 Ом \)

Смешанное соединение проводников
Показать ответ Показать решение Видеорешение

Ответ: \(I_{1}=6 А \)

Амперметр \(A_2 \) показывает силу тока в резисторе \(R_{1} \)

Амперметр \(A_1 \) показывает силу тока всей цепи, так как \(R_3\) и участок \(R_{12} \) соединены последовательно.

Сила тока параллельного участка \(R_{12} \) равна \(I=9 А \)

1) Найдем сопротивление \(R_{12} \):

Дано: \( R_1=3 Ом \)

\( R_2=6 Ом \)

\(I=9 А \)

\(I_{1}-?\)

\( \dfrac{1}{ R_{12}}= \dfrac{1}{R_1}+ \dfrac{1}{R_2} \)

\( \dfrac{1}{ R_{12}}= \dfrac{1}{3}+ \dfrac{1}{6} \)

\( \dfrac{1}{ R_{12}}= \dfrac{\; \; 1^{(2 } }{3\;}+ \dfrac{\;\; 1^{(1} }{6\;} \)

\( \dfrac{1}{ R_{12}}= \dfrac{2+1}{6} \)

\( \dfrac{1}{ R_{12}}= \dfrac{3}{6} \)

\( \dfrac{1}{ R_{12}}= \dfrac{1}{2} \)

\( R_{12}=2 Ом \)

2)Найдем напряжение участка \(R_{12} \):

\(U_{12}= R_{12}\cdot I= 2 Ом \cdot 9 А=18 В \)

Напряжение на каждом из резисторов параллельного участка одинаково и равно \(U_{12} \)

\(U_{1}=U_{2}=U_{12}=18 В \)

\(I_{1}=\dfrac{U_{1}}{R_{1}}=\dfrac{18 \; В}{3 \;Ом }=6 А \)

Ответ: \( I_{1}=6 А \)

ПОЗЖЕ

Задача 2. ( Расчет электрических схем)
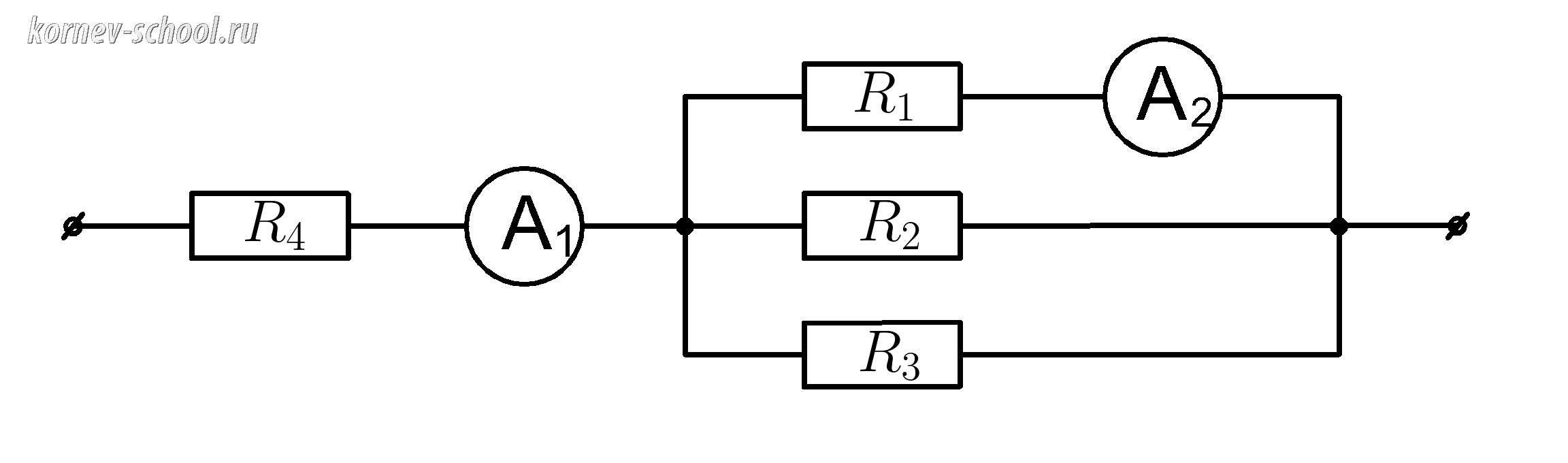
На схеме изображенной на рисунке амперметр \(A_1 \) показывает силу тока \(I=1 А \) , определить показания амперметра \(A_2 \) , если \(R_1=80 Ом \; , \; R_2=70 Ом , \; R_3=28 Ом , \; R_4=2 Ом \)

Смешанное соединение проводников
Показать ответ Показать решение Видеорешение

Ответ: \(I_{1}=0,2 А \)

Амперметр \(A_1 \) показывает силу тока всей цепи, так как \(R_4\) и участок \(R_{123} \) соединены последовательно.

Сила тока параллельного участка \(R_{123} \) равна \(I=1 А \)

1) Найдем сопротивление \(R_{123} \):

Дано: \( R_1=80 Ом \)

\( R_2=70 Ом \)

\( R_3=28 Ом \)

\(I_{1}-?\)

\( \dfrac{1}{ R_{123}}= \dfrac{1}{R_1}+ \dfrac{1}{R_2}+ \dfrac{1}{R_3} \)

\( \dfrac{1}{ R_{123}}= \dfrac{1}{80}+ \dfrac{1}{70} +\dfrac{1}{28} \)

\( \dfrac{1}{ R_{123}}= \dfrac{\; \; 1^{(7 } }{80\;}+ \dfrac{\;\; 1^{(8} }{70\;} +\dfrac{\;\;1^{(20}}{28} \)

\( \dfrac{1}{ R_{123}}= \dfrac{7+8+20}{560} \)

\( \dfrac{1}{ R_{123}}= \dfrac{35}{560} \)

\( \dfrac{1}{ R_{123}}= \dfrac{35}{560} \)

\( R_{123}= \dfrac{560}{35}=16 Ом \)

2)Найдем напряжение участка \(R_{123} \):

\(U_{123}= R_{123}\cdot I= 16 Ом \cdot 1А=16 В \)

Напряжение на каждом из резисторов параллельного участка одинаково и равно \(U_{123} \)

\(U_{1}=U_{2}=U_{3}=U_{123}=16 В \)

\(I_{1}=\dfrac{U_{1}}{R_{1}}=\dfrac{16 \; В}{80 \;Ом }=0,2 А \)

Ответ: \( I_{1}=0,2 А \)

ПОЗЖЕ

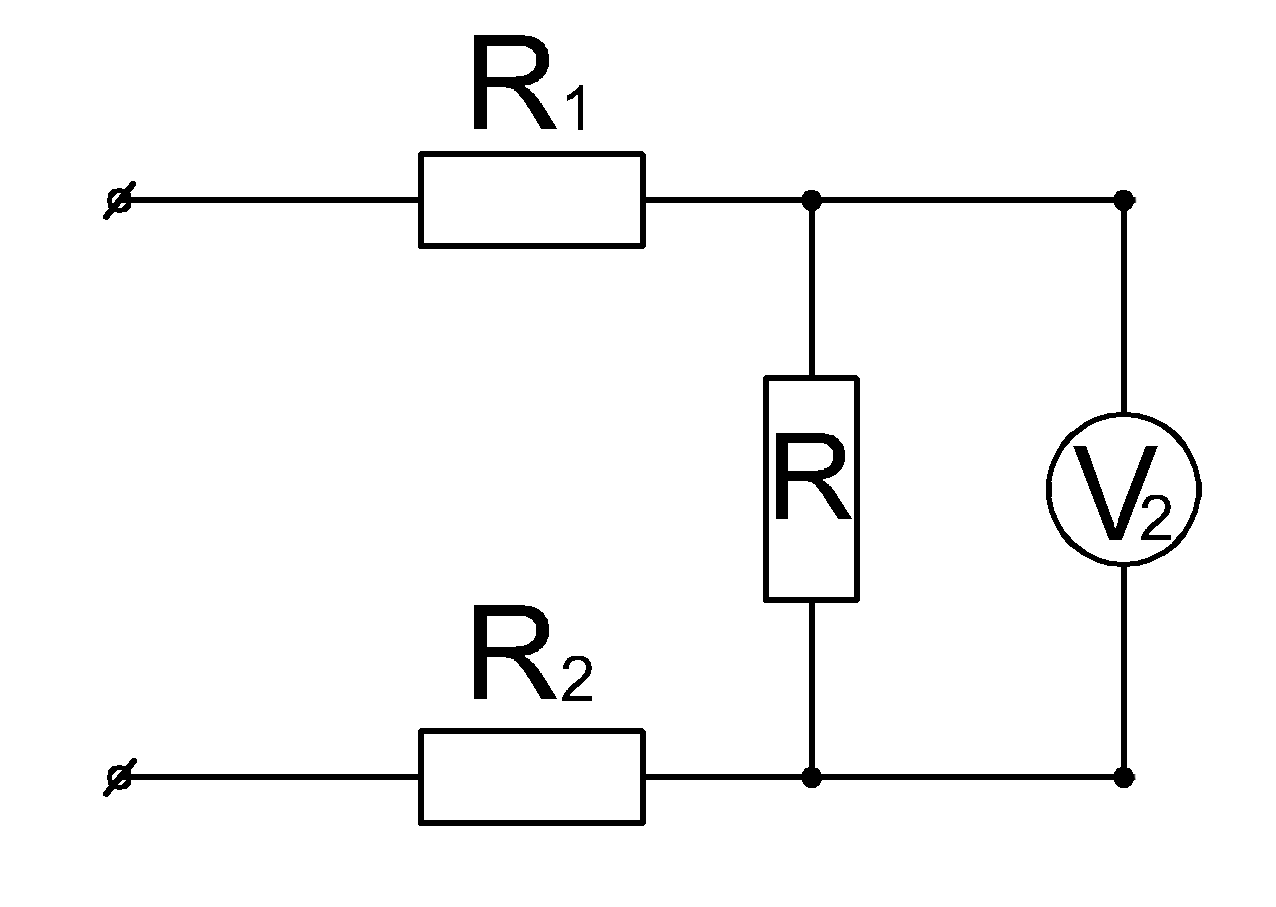
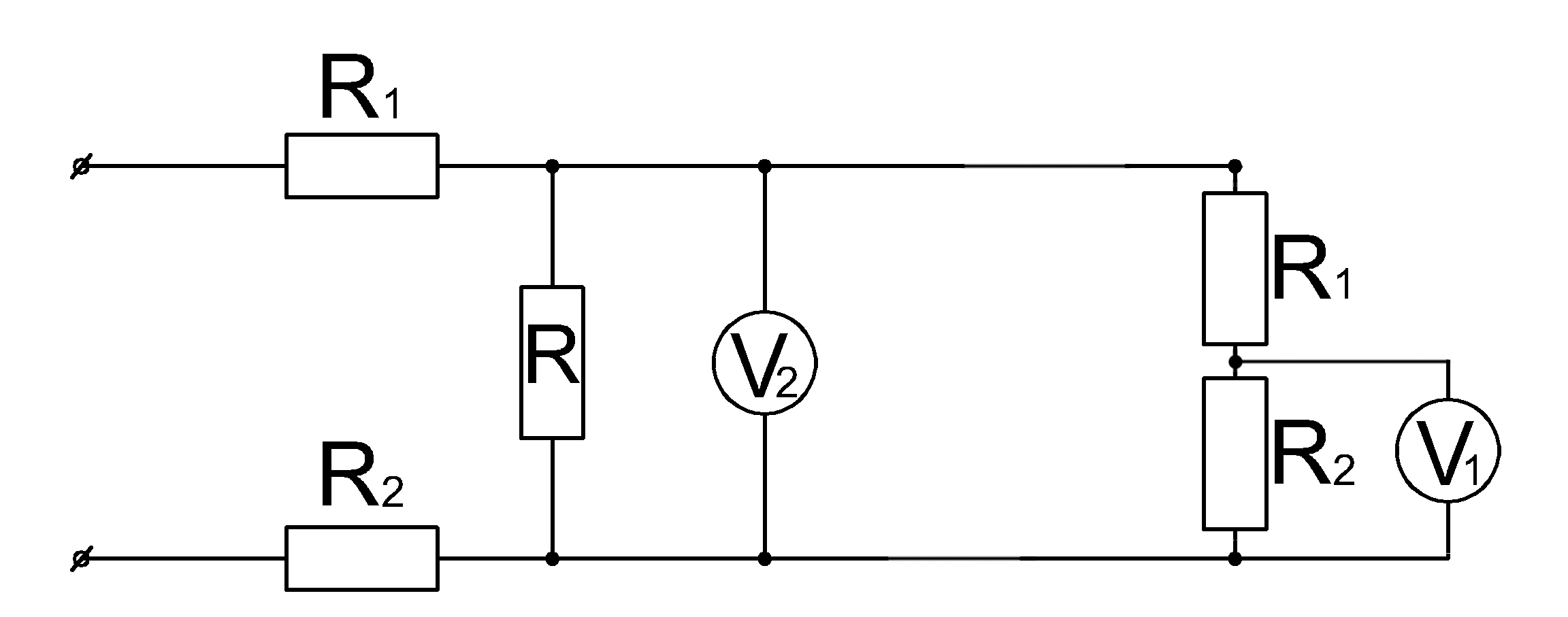
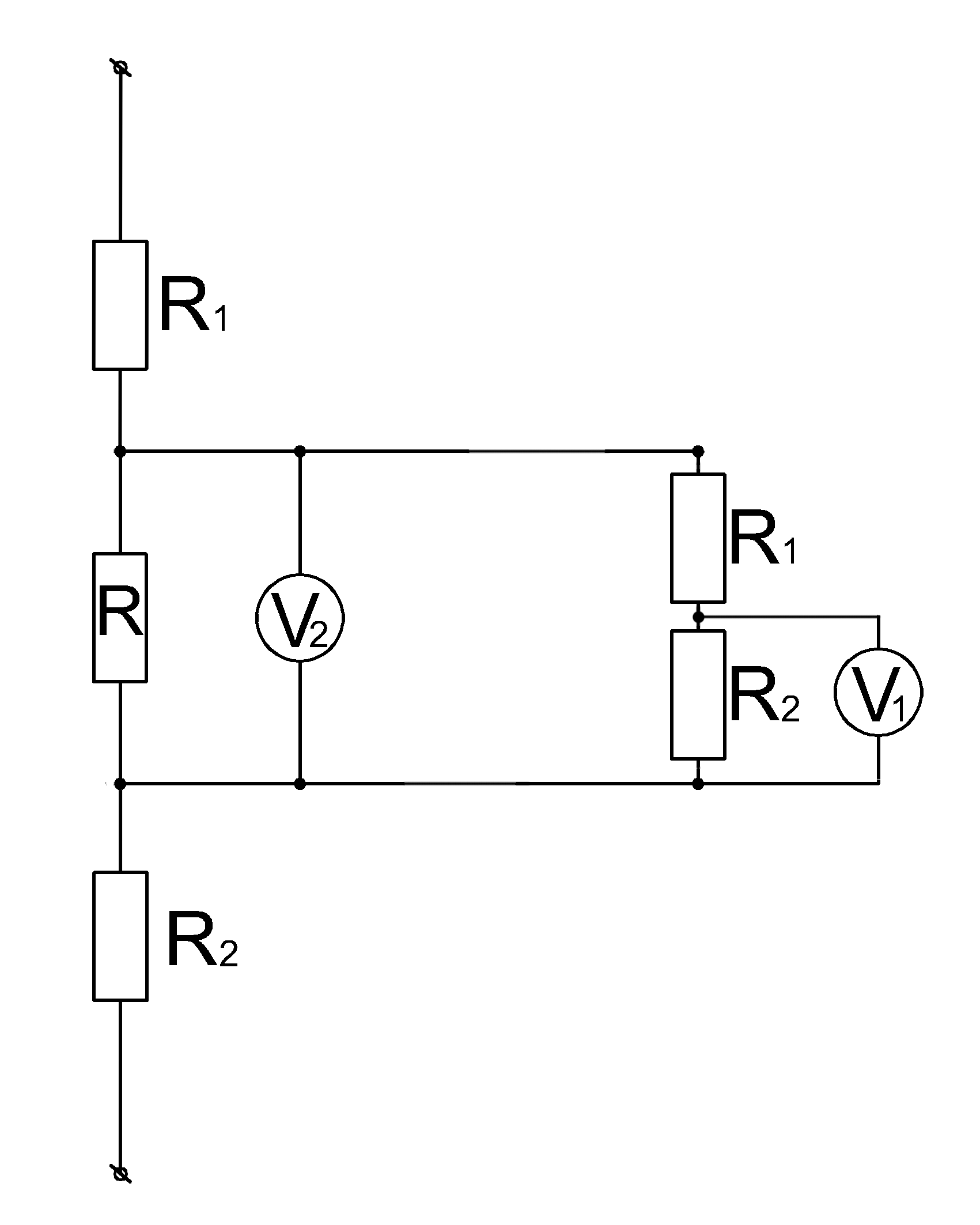
Задача 21. ( Расчет электрических схем)

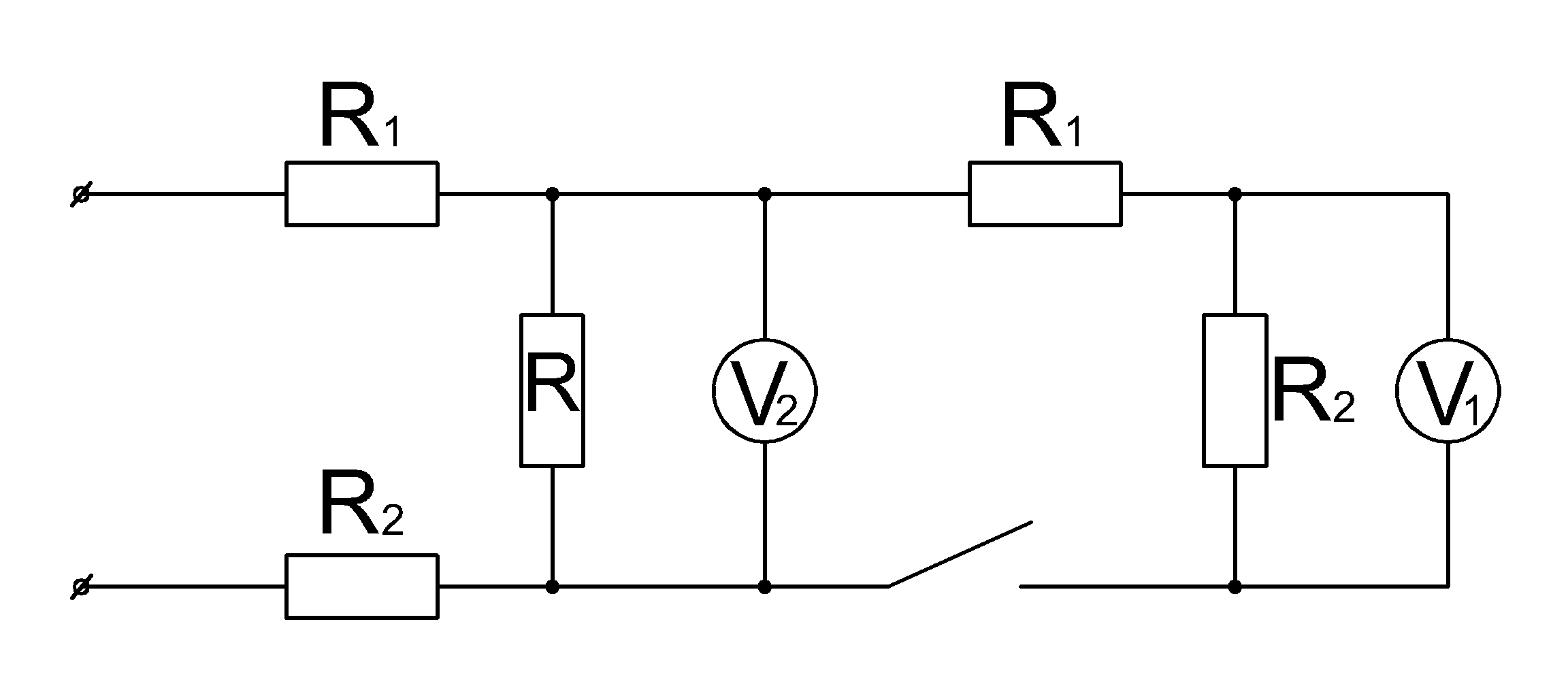
На контакты цепи подается напряжение \(U=25 \ Вольт \).
При замкнутом ключе вольтметр \(V_2\) показывает напряжение \(U_2=10 \ Вольт \), а показания вольтметра \(V_1 \) составляют \(U_1=1 \ Вольт \).
Если разомкнуть ключ, то вольтметр \(V_2 \) будет показывать напряжение 5 Вольт.
Сопротивление резистора \( R \) равняется 100 Ом. Найти сопротивление резистора \( R_2 \)

Показать ответ Показать решение Видеорешение

Ответ: \( R_2=40 \ \ Ом \)

Если ключ разомкнут, то ток через правую часть схемы не течет.
Для простоты просто уберем правую часть схемы вместе с ключом:

Перересуем эту схему в более удобном виде и уберем вольтметр,
он был нужен лишь для того, чтобы показывать напряжение на резисторе \( R, \) которое равно пяти вольтам при разомкнутом ключе

Составим закон Ома для резистора \( R \ : \)

\(I= \dfrac{U_5}{R} = \dfrac{5 \ В }{100 \ Ом}= 0,05 \ A \)

Мы имеем дело с последовательным соединением, поэтому сила тока всей этой цепи равна 0,05 Ампер

Составим закон Ома для этой цепи:

\( I= \dfrac{U}{R_1+R+R_2} \)

Вставим числа в эту формулу:

\( 0,05 = \dfrac{25}{R_1+100+R_2} \)

\( 0,05(R_1+100+R_2) = 25 \)

\( R_1+100+R_2 = \dfrac{25}{0,05} \)

\( R_1+100+R_2 = \dfrac{25}{0,05} \)

\( R_1+100+R_2 = 500 \)

\( R_1+R_2 = 500 -100 \)

\( R_1+R_2 = 400 \)

То есть все, что мы можем почерпнуть из ситуации, когда ключ разомкнут это то, что сумма сопротивлений первого и второго резистора равняется 400 Ом.

\( R_1+R_2 = 400 \ Ом \)
Далее расмотрим схему при замкнутом ключе, немного упростив ее, убрав ключ:

и еще упростим:

Показания вольтметра \(V_1:\)

\(U_1=1 \ Вольт \)

Показания вольтметра \(V_2:\)

\(U_2=10 \ Вольт \)

Напряжение на параллельном участке равно \(U_2=10 \ Вольт \)

а напряжение на правом резисторе \(R_2 \) равно 1 Вольт, значит напряжение на правом резисторе \(R_1\) равно 9 Вольт

Сила тока в этих двух резисторах одинакова, так как они соединены последовательно

запишем закон Ома для них:

\(I=\dfrac{1}{R_2} \ \ \ \ \ \ \ \ \ \ \ \ I=\dfrac{9}{R_1} \)

\( \dfrac{1}{R_2} = \dfrac{9}{R_1} \)

\( R_1=9R_2 \)

\( R_1+R_2 = 400 \)
\( 9R_2+R_2 = 400 \)

\( 10R_2 = 400 \)

\( R_2 = 40 \)

Ответ: \( R_2 = 40 \ Ом \)

ПОЗЖЕ