Смешанное соединение проводников .
Репетитор по физике
8 916 478 10 32
Задача 1. (Смешанное соединение проводников)
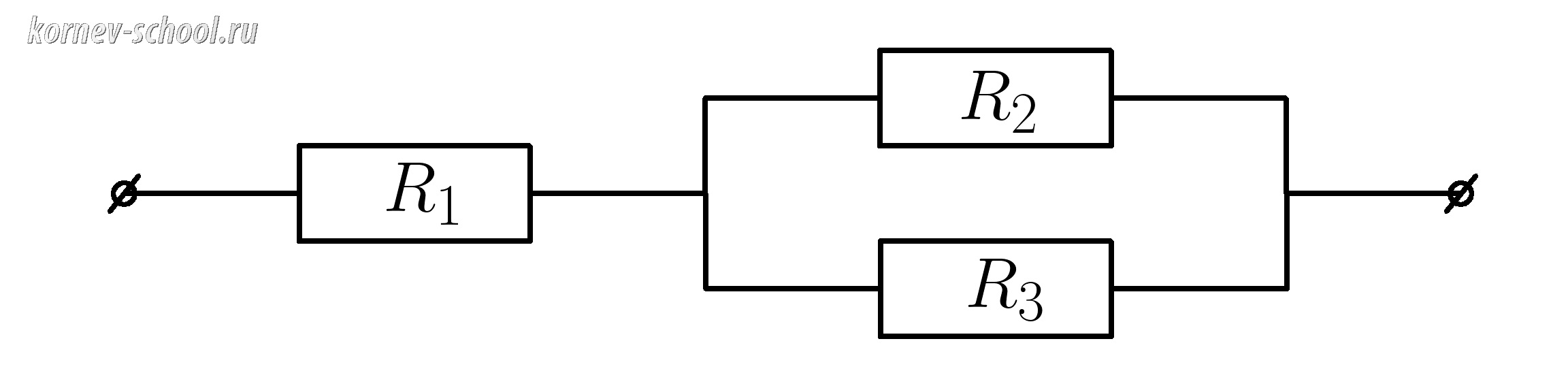
Найти сопротивление цепи, если \(R_1=2 Ом \; , \; R_2=2 Ом , \; R_3=2 Ом\)
Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=3 \; Ом \)
Запишем формулу параллельного соединения для двух проводников:
Дано: \( R_1=2 Ом \)
\( R_2=2 Ом \)
\( R_3=2 Ом \)
\(R_{общ}-?\)
\( \dfrac{1}{ R_{23}}= \dfrac{1}{R_2}+ \dfrac{1}{R_3} \)
\( \dfrac{1}{ R_{23}}= \dfrac{1}{2}+ \dfrac{1}{2} \)
\( \dfrac{1}{ R_{23}}= \dfrac{2}{2} \)
\( \dfrac{1}{ R_{23}}= 1 \)
\( R_{23}= 1 Ом \)
\( R_{общ}=R_{1}+R_{23}=2 Ом+1 Ом=3 Ом \)
Ответ: \( R_{общ}= 3 \; Ом \)
Задача 2. (Смешанное соединение проводников)
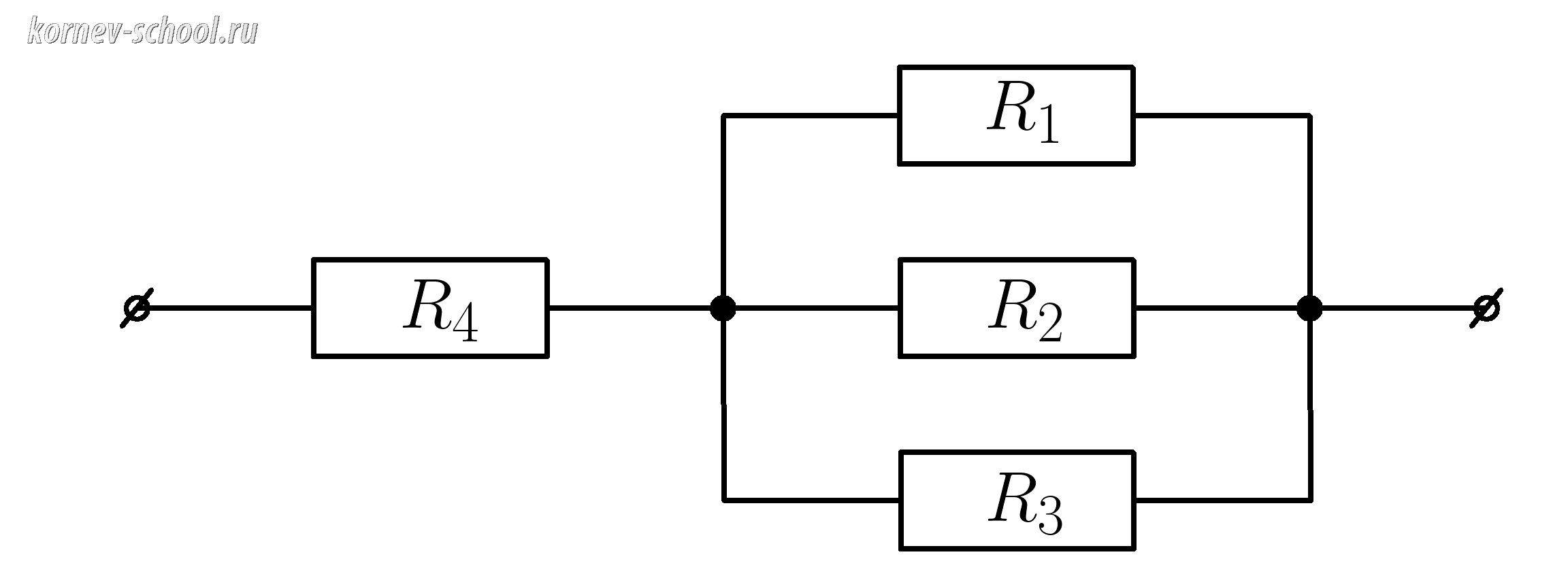
Найти сопротивление цепи, если \(R_1=18 Ом \; , \; R_2=18 Ом , \; R_3=18 Ом, \; R_4=2 Ом\)
Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=8 \; Ом \)
Можно запомнить, что если два и более резистора соединены параллельно и сопротивления этих
резисторов одинаковые, то сопротивление параллельного участка будет равно сопротивлению любого из этих
резисторов деленное на их количество.
Дано: \( R_1=18 Ом \)
\( R_2=18 Ом \)
\( R_3=18 Ом \)
\( R_4=2 Ом \)
\(R_{общ}-?\)
\( R_{123}=\dfrac{18 Ом}{3}=6 Ом \)
\( R_{общ}=R_{4}+R_{123}=2 Ом+6 Ом=8 Ом \)
Ответ: \( R_{общ}= 8 \; Ом \)
Задача 3. (Смешанное соединение проводников)
Найти сопротивление цепи, если \(R_1=6 Ом \; , \; R_2=2 Ом , \; R_3=1 Ом , \; R_4=1,4 Ом \)

Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=2 \; Ом \)
Запишем формулу параллельного соединения для трех проводников:
Дано: \( R_1=6 Ом \)
\( R_2=2 Ом \)
\( R_3=1 Ом \)
\( R_4=1,4 Ом \)
\(R_{общ}-?\)
\( \dfrac{1}{ R_{123}}= \dfrac{1}{R_1}+ \dfrac{1}{R_2}+ \dfrac{1}{R_3} \)
\( \dfrac{1}{ R_{123}}= \dfrac{1}{6}+ \dfrac{1}{2} +\dfrac{1}{1} \)
\( \dfrac{1}{ R_{123}}= \dfrac{\; \; 1^{(1 } }{6\;}+ \dfrac{\;\; 1^{(3} }{2\;} +\dfrac{\;\;1^{(6}}{1} \)
\( \dfrac{1}{ R_{123}}= \dfrac{1+3+6}{6} \)
\( \dfrac{1}{ R_{123}}= \dfrac{10}{6} \)
\( R_{123}= \dfrac{6}{10}=0,6 Ом \)
\( R_{общ}=R_{4}+R_{123}=1,4 Ом+0,6 Ом=2 Ом \)
Ответ: \( R_{общ}= 2 \; Ом \)
Задача 5. (Смешанное соединение проводников)
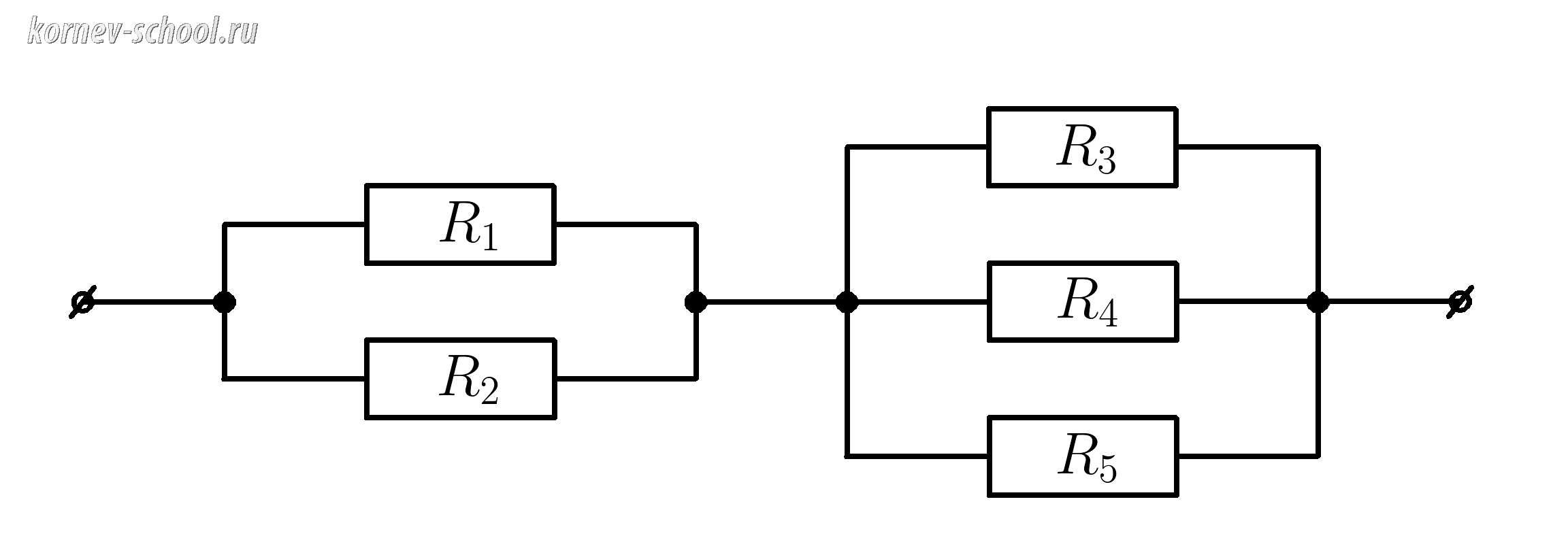
Найти сопротивление цепи, если \(R_1=15 Ом \; , \; R_2=5 Ом , \; R_3=2 Ом , \; R_4=4 Ом , \; R_5=7 Ом \)
Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=4,87 \; Ом \)
Участок \( R_{12}\) и участок \( R_{345} \) соединены последовательно.
Запишем формулу параллельного соединения для трех проводников:
Дано: \( R_1=15 Ом \)
\( R_2=5 Ом \)
\( R_3=2 Ом \)
\( R_4=4 Ом \)
\( R_5=7 Ом \)
\(R_{общ}-?\)
\( \dfrac{1}{ R_{345}}= \dfrac{1}{R_3}+ \dfrac{1}{R_4}+ \dfrac{1}{R_5} \)
\( \dfrac{1}{ R_{345}}= \dfrac{1}{2}+ \dfrac{1}{4} +\dfrac{1}{7} \)
\( \dfrac{1}{ R_{345}}= \dfrac{\; \; 1^{(14 } }{2\;}+ \dfrac{\;\; 1^{(7} }{4\;} +\dfrac{\;\;1^{(4}}{7} \)
\( \dfrac{1}{ R_{345}}= \dfrac{14+7+4}{28} \)
\( \dfrac{1}{ R_{345}}= \dfrac{25}{28} \)
\( R_{345}= \dfrac{28}{25}=1,12 Ом \)
\( \dfrac{1}{ R_{12}}= \dfrac{1}{R_1}+ \dfrac{1}{R_2} \)
\( \dfrac{1}{ R_{12}}= \dfrac{1}{15}+ \dfrac{1}{5} \)
\( \dfrac{1}{ R_{12}}= \dfrac{\; \; 1^{(1 } }{15\;}+ \dfrac{\; 1^{(3} }{5\;} \)
\( \dfrac{1}{ R_{12}}= \dfrac{1+3}{15} \)
\( \dfrac{1}{ R_{12}}= \dfrac{4}{15} \)
\( R_{12}= \dfrac{15}{4}=3,75 Ом \)
\( R_{общ}=R_{12}+ R_{345}= 3,75 Ом +1,12 Ом=4,87 \; Ом \)
Ответ: \( R_{общ}= 4,87 \; Ом \)
Задача 6. (Смешанное соединение проводников)
Найти сопротивление цепи, если \(R_1=6 Ом \; , \; R_2=6 Ом , \; R_3=14 Ом , \; R_4=60 Ом , \; R_5=84 Ом \)

Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=13 \; Ом \)
Участок \( R_{12}\) и участок \( R_{345} \) соединены последовательно.
Запишем формулу параллельного соединения для трех проводников:
Дано: \( R_1=6 Ом \)
\( R_2=6 Ом \)
\( R_3=14 Ом \)
\( R_4=60 Ом \)
\( R_5=84 Ом \)
\(R_{общ}-?\)
\( \dfrac{1}{ R_{345}}= \dfrac{1}{R_3}+ \dfrac{1}{R_4}+ \dfrac{1}{R_5} \)
\( \dfrac{1}{ R_{345}}= \dfrac{1}{14}+ \dfrac{1}{60} +\dfrac{1}{84} \)
\( \dfrac{1}{ R_{345}}= \dfrac{\; \; 1^{(30 } }{14\;}+ \dfrac{\;\; 1^{(7} }{60\;} +\dfrac{\;\;1^{(5}}{84} \)
\( \dfrac{1}{ R_{345}}= \dfrac{30+7+5}{420} \)
\( \dfrac{1}{ R_{345}}= \dfrac{42}{420} \)
\( R_{345}= \dfrac{420}{42}=10 Ом \)
\( R_{12}= \dfrac{1}{R_1}+ \dfrac{1}{R_2} \)
\( \dfrac{1}{ R_{12}}= \dfrac{1}{6}+ \dfrac{1}{6} \)
\( \dfrac{1}{ R_{12}}= \dfrac{2}{6} \)
\( \dfrac{1}{ R_{12}}= \dfrac{1}{3} \)
\( R_{12}= 3 Ом \)
\( R_{общ}=R_{12}+ R_{345}= 3 Ом +10 Ом=13 \; Ом \)
Ответ: \( R_{общ}= 13 \; Ом \)
Задача 7. (Смешанное соединение проводников)
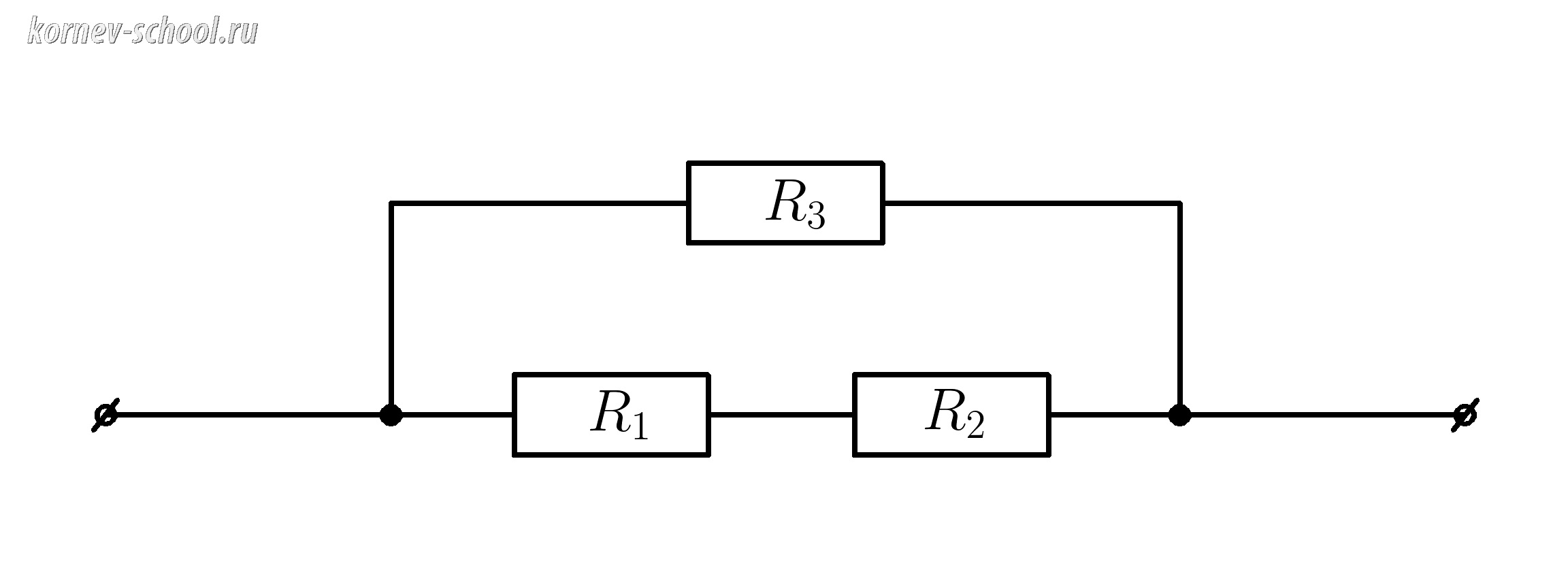
Найти сопротивление цепи, если \(R_1=12 Ом \; , \; R_2=2 Ом , \; R_3=35 Ом \)
Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=10 \; Ом \)
Участок \( R_{12}\) и \( R_{3} \) соединены параллельно .
Дано: \( R_1=12 Ом \)
\( R_2=2 Ом \)
\( R_3=35 Ом \)
\(R_{общ}-?\)
\( R_{12}= R_1+R_2=12 Ом+ 2 Ом=14 Ом \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{R_{12}}+ \dfrac{1}{R_3} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{14}+ \dfrac{1}{35} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{\;\;1^{(5}}{14}+ \dfrac{\;\;1^{(2}}{35} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{5+2}{70} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{7}{70} \)
\( R_{общ}= \dfrac{70}{7}= 10 Ом \)
Ответ: \( R_{общ}= 10 \; Ом \)
Задача 8. (Смешанное соединение проводников)
Найти сопротивление цепи, если \(R_1=50 Ом \; , \; R_2=10 Ом , \; R_3=15 Ом \)

Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=12 \; Ом \)
Участок \( R_{12}\) и \( R_{3} \) соединены параллельно .
Дано: \( R_1=50 Ом \)
\( R_2=10 Ом \)
\( R_3=15 Ом \)
\(R_{общ}-?\)
\( R_{12}= R_1+R_2=50 Ом+ 10 Ом=60 Ом \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{R_{12}}+ \dfrac{1}{R_3} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{60}+ \dfrac{1}{15} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{\;\;1^{(1}}{60}+ \dfrac{\;\;1^{(4}}{60} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1+4}{60} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{5}{60} \)
\( R_{общ}= \dfrac{60}{5}= 12 Ом \)
Ответ: \( R_{общ}= 12 \; Ом \)
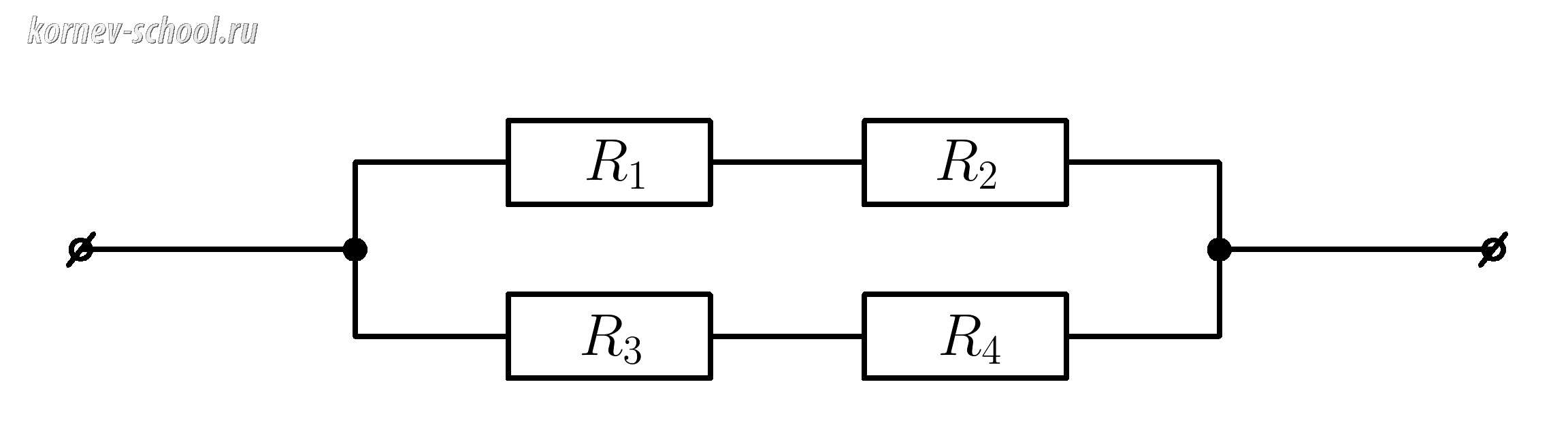
Задача 9. (Смешанное соединение проводников)
Найти сопротивление цепи, если \(R_1= 5 Ом \; , \; R_2=3 Ом , \; R_3=29 Ом , \; R_4=27 Ом \)
Показать ответ
Показать решение
Видеорешение
Ответ: \(R_{общ}=7 \; Ом \)
Участок \( R_{12}\) и \( R_{34} \) соединены параллельно .
Дано: \( R_1=5 Ом \)
\( R_2=3 Ом \)
\( R_3=29 Ом \)
\( R_4=27 Ом \)
\(R_{общ}-?\)
\( R_{12}= R_1+R_2=5 Ом+ 3 Ом=8 Ом \)
\( R_{34}= R_3+R_4=29 Ом+ 27 Ом=56 Ом \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{R_{12}}+ \dfrac{1}{R_{34}} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{1}{8}+ \dfrac{1}{56} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{\;\;1^{(7}}{8}+ \dfrac{\;\;1^{(1}}{56} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{7+1}{56} \)
\( \dfrac{1}{ R_{общ}}= \dfrac{8}{56} \)
\( R_{общ}= \dfrac{56}{8}= 7 Ом \)
Ответ: \( R_{общ}= 7 \; Ом \)
|







