Движение связанных тел.
Когда мы имеем дело с системмой связанных нитью тел нам удобнее рассматривать не всю систему целиком, а каждое тело по отдельности.
Задача 1 (Движение связанных тел)
На неподвижном блоке с разных сторон подвешены на нити грузы массами \(m_1=2 \ кг \) и \(m_2=3 \ кг \).
С каким ускорением движутся грузы?
\(g=10 м/с^2\)
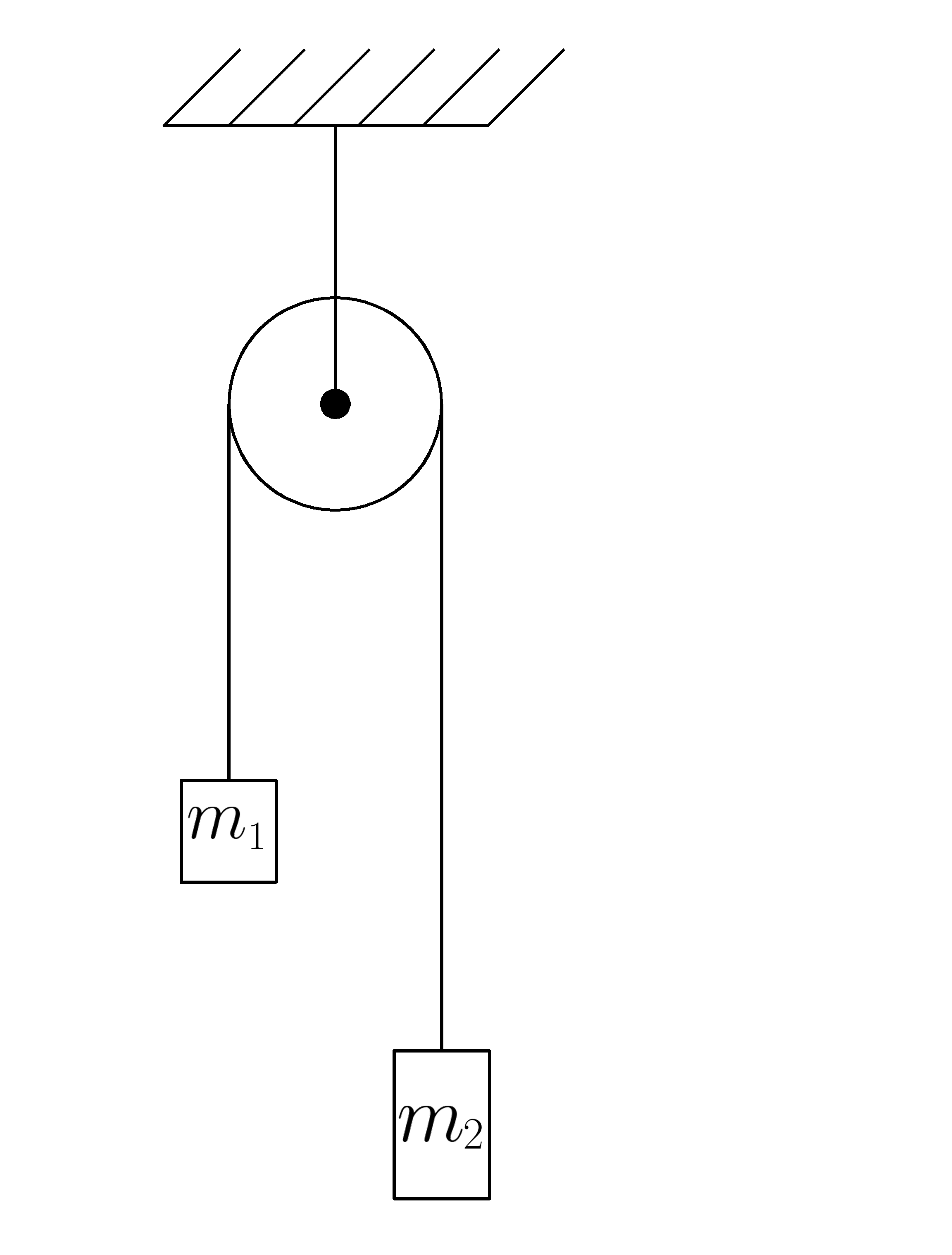
Показать ответ Показать решение Видеорешение
Задача 2 (Движение связанных тел)
Через неподвижный блок перекинута нить, к противоположным концах которой привязаны два груза. Масса первого груза \( m_1= 1 кг \), масса второго груза \( m_2=19 кг \). Найти силу натяжения нити \(T . \)
\(g=10 м/с^2 \)

Показать ответ Показать решение Видеорешение
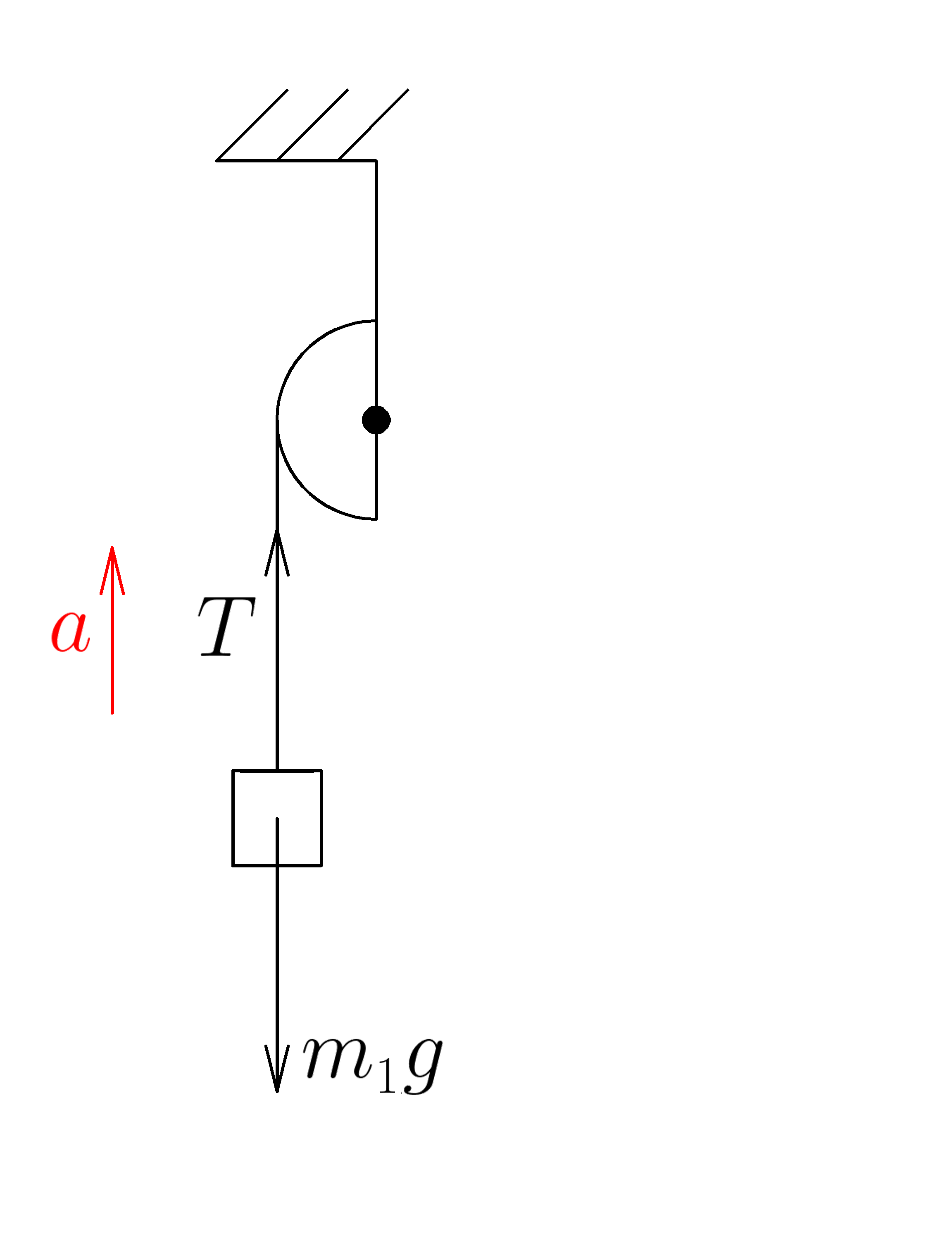
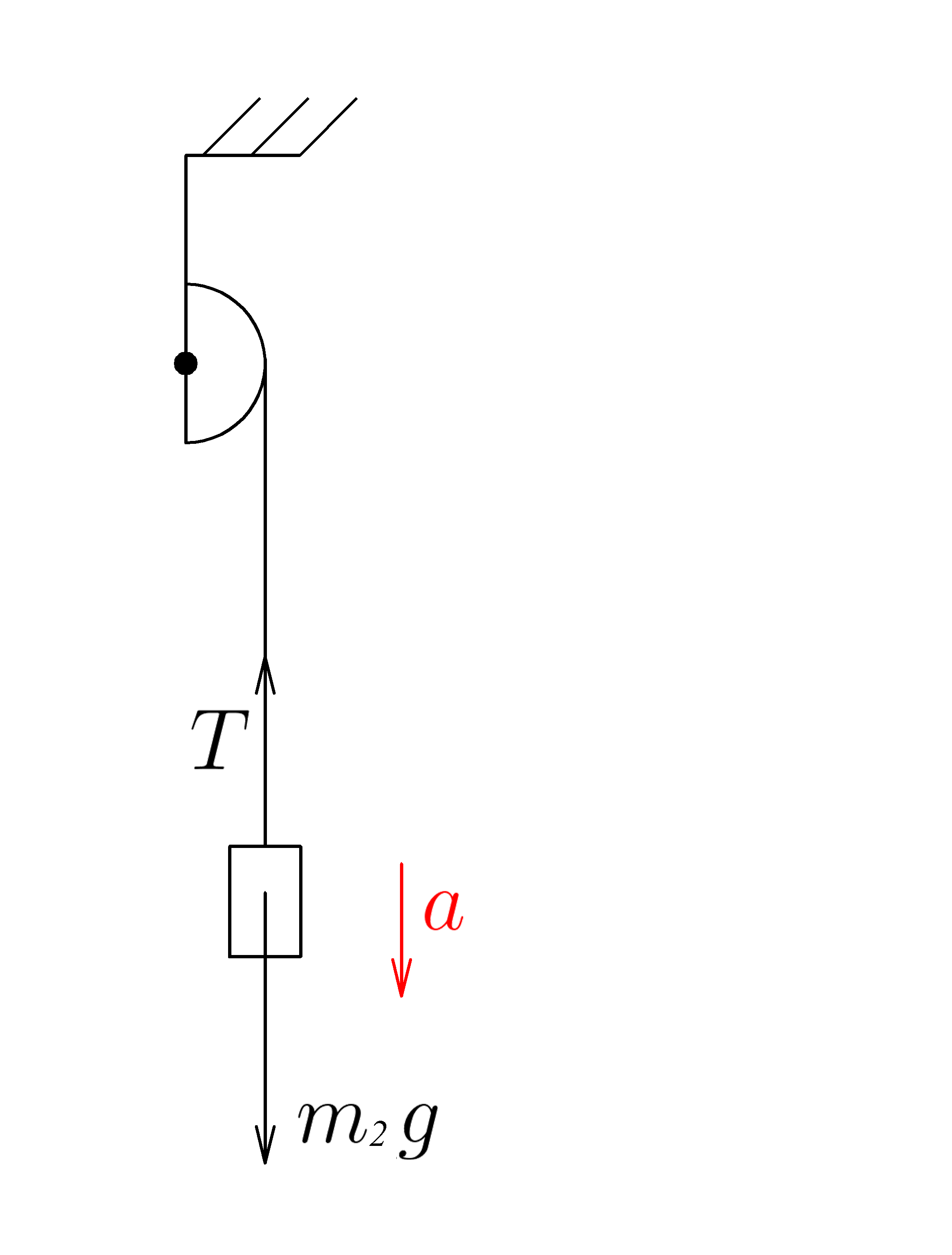 Запишем уравнение второго закона Ньютона для правого груза:
Запишем уравнение второго закона Ньютона для правого груза: