Задачи на цилиндр .

Если вращать прямоугольник вокруг любой из его сторон, то получится цилиндр.

На фото цилиндр выглядит вот так:

На чертеже цилиндр обозначают так:

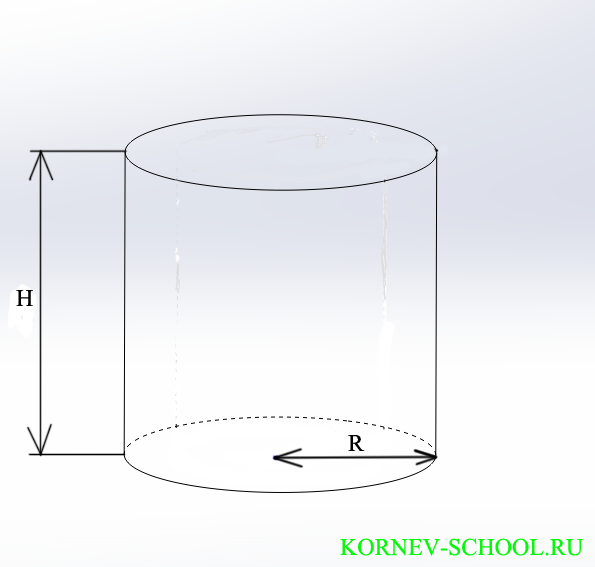
\( R \) радиус цилиндра

\( H \) высота цилиндра

Объем цилиндра вычисляется по формуле:

\( V=S \cdot H \)

\(S\) площадь основания цилиндра

любой цилиндр имеет два одинаковых основания, нижнее и верхнее

каждое основание цилиндра это круг

Как мы помним площадь круга находится по формуле: \( S=\pi \cdot R^2 \)

Заменим в формуле вычисления объема цилиндра \( S \) на \( \pi \cdot R^2 \) и мы сможем находить объем цилиндра зная его радиус и высоту:

\( V=S \cdot H = \pi \cdot R^2 \cdot H \)

\( \textcolor {green} { V= \pi \cdot R^2 \cdot H } \)

Задача 1:

Найдите объем цилиндра высотой 5 см и площадью основания \( S=3 \ см^2 \)
Показать ответ Показать решение Видеорешение

\( V=15 \ см^3 \)

\( V=H \cdot S=5 \ см \cdot 3 \ см^2= 15 \ см^3 \)

ПОЗЖЕ

Задача 2:

Каким будет объем цилиндра, если его высота \(H=1 \ см \), а радиус основания \(R=1 \ см \) ?
Показать ответ Показать решение Видеорешение

\( V=\pi см^3 \)

\( V= \pi \cdot R^2 \cdot H = \pi \cdot (1 \ см)^{2} \cdot 1 \ см = \pi см^3 \)

Ответ: \( V=\pi см^3 \)

ПОЗЖЕ