Метод координат для пирамиды .

1. \( ABCD \) - треугольная пирамида, все грани которой являются равносторонними треугольниками с единичной стороной. \(Q\)- середина стороны \(AB\)
\(P\)- середина стороны \(BC . \) Найдите угол между прямыми \( DP \) и \(QC\)
Показать ответ Показать решение Видеорешение

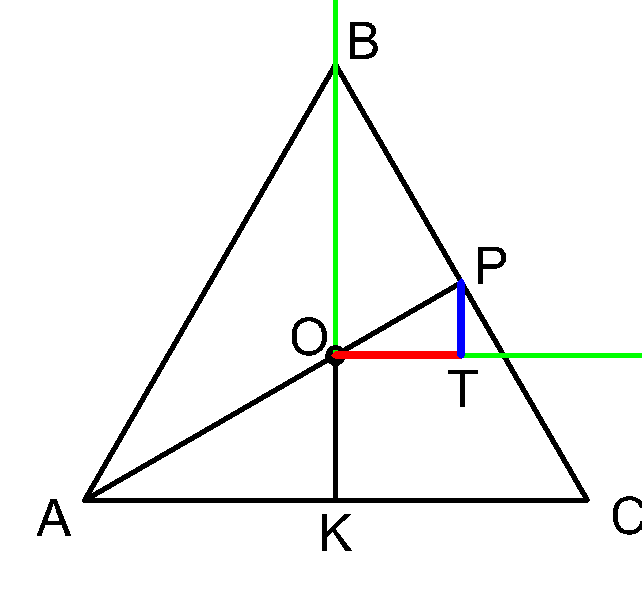
Пусть основанием нашей пирамиды будет равносторонний треугольник \(ABC\) поместим начало координат в центр вписанной окружности, а оси расположим как мы привыкли:

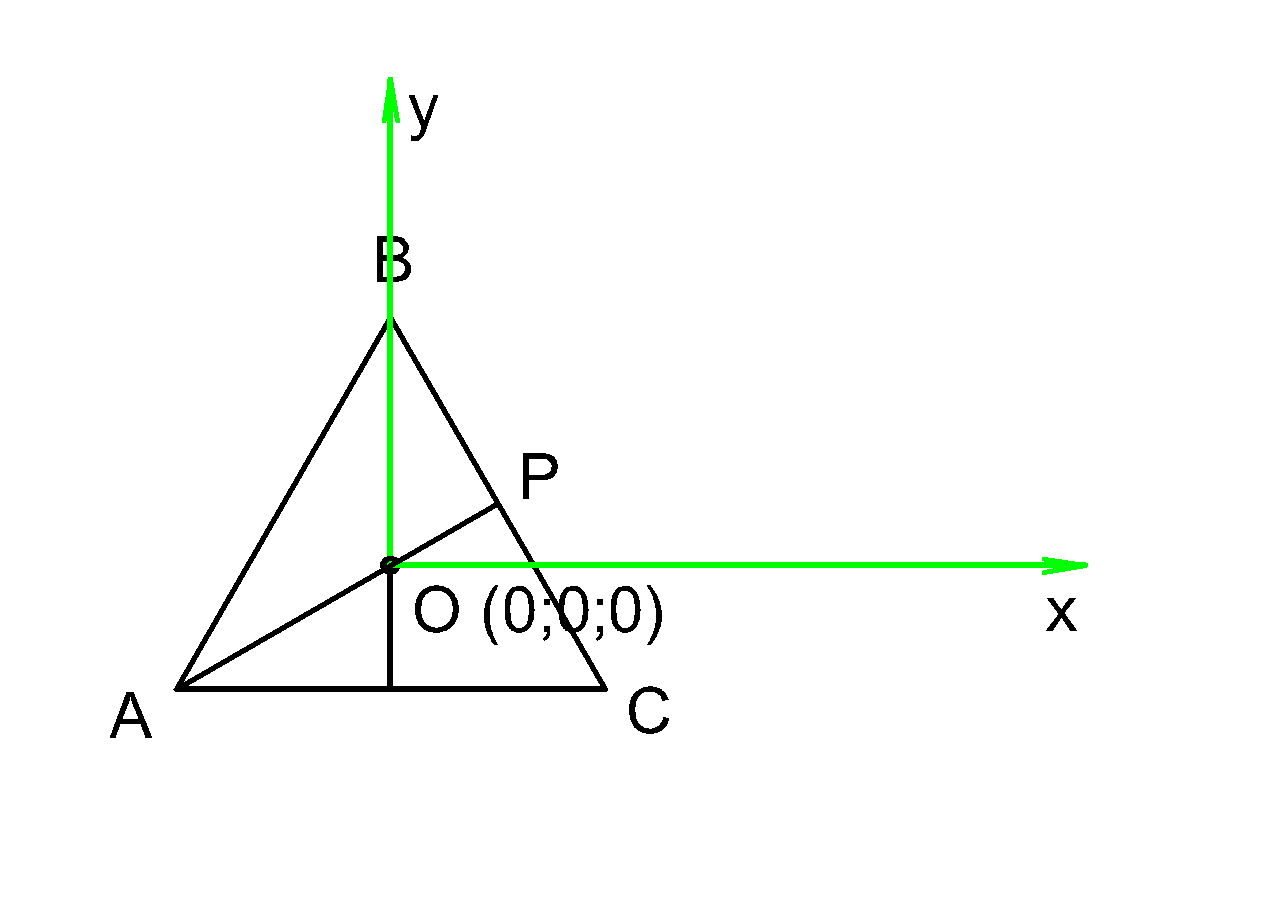
Ось \( Z \) также начинается в точке \(O\) и проходит через вершину \(D \) нашей пирамиды, то есть направлена вертикально вверх, поэтому на этом плоскостном рисунке мы ее не видим.
Попробуем найти координаты точки \( P: \)

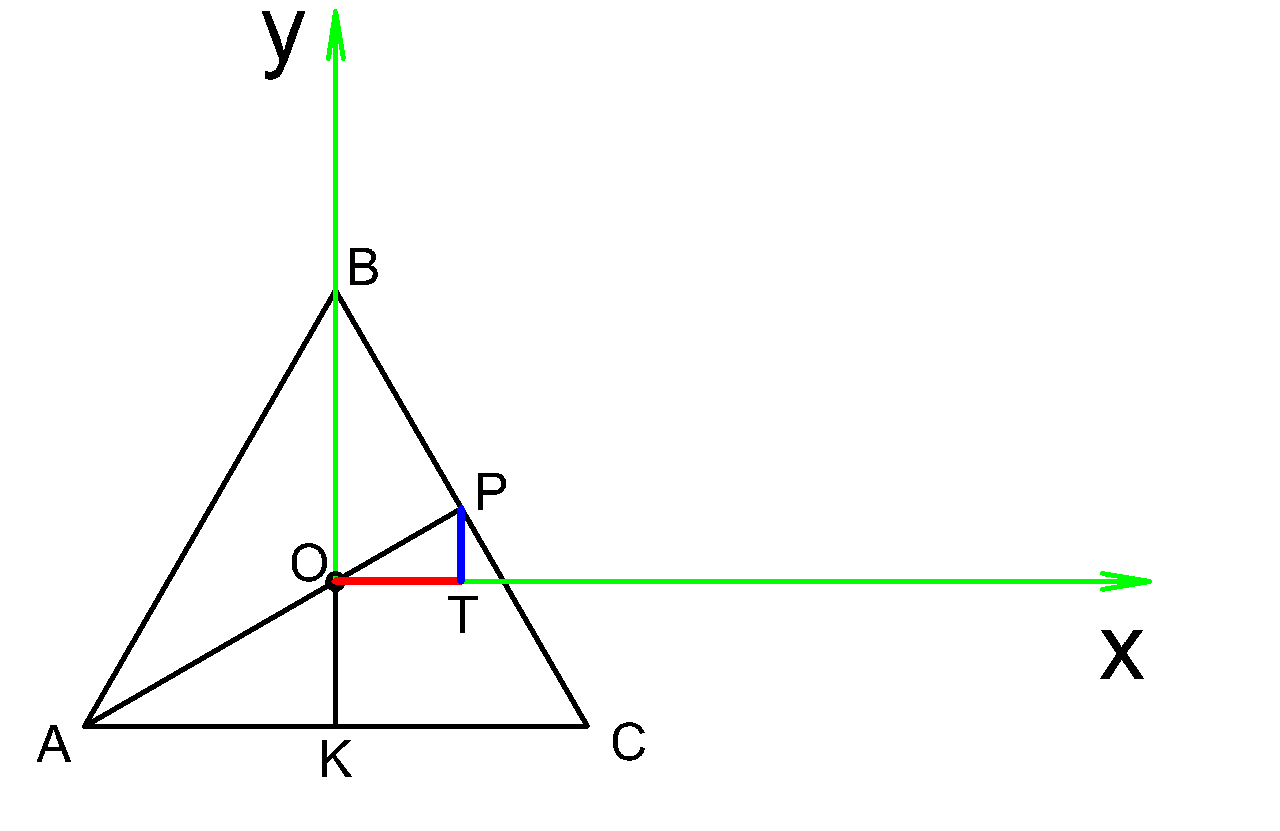
Получается длина красного отрезка \( OT \) равна абсциссе точки \( P \) , а длина синего отрезка \(PT \) равна ординате точки \( P \)

Мы знаем, что любое ребро нашей пирамиды равно единице, значит \(КС= \dfrac{1}{2} . \)
Найдем \(BK \) по теореме Пифагора:
\(BK= \sqrt{ 1^2- \left( \dfrac{1}{2} \right )^2 } = \dfrac{\sqrt{3}}{2} \)
Центр вписаной окружности делит высоту в соотношении 2:1 от вершины треугольника:
\(BO=2x \)
\(OK=x \)
\(2x+x=\dfrac{\sqrt{3}}{2} \)
\(x=\dfrac{\sqrt{3}}{6} = OK\)
\(OP\) в два раза меньше \( AO \) по тому же принципу.
\( \angle TOP=\angle OAK \) (по теореме о параллельных прямых и секущей)
Поэтому треугольники \( TOP \) и \( OAK \) подобны по двум углам с коэффициентом подобия 2.
Значит \(OT\) в 2 раза меньше \(AK\)
\( OT=\dfrac{1}{4} \)
\(PT\) в 2 раза меньше \(OK\)
\(PT=\dfrac{\sqrt{3}}{12} \)
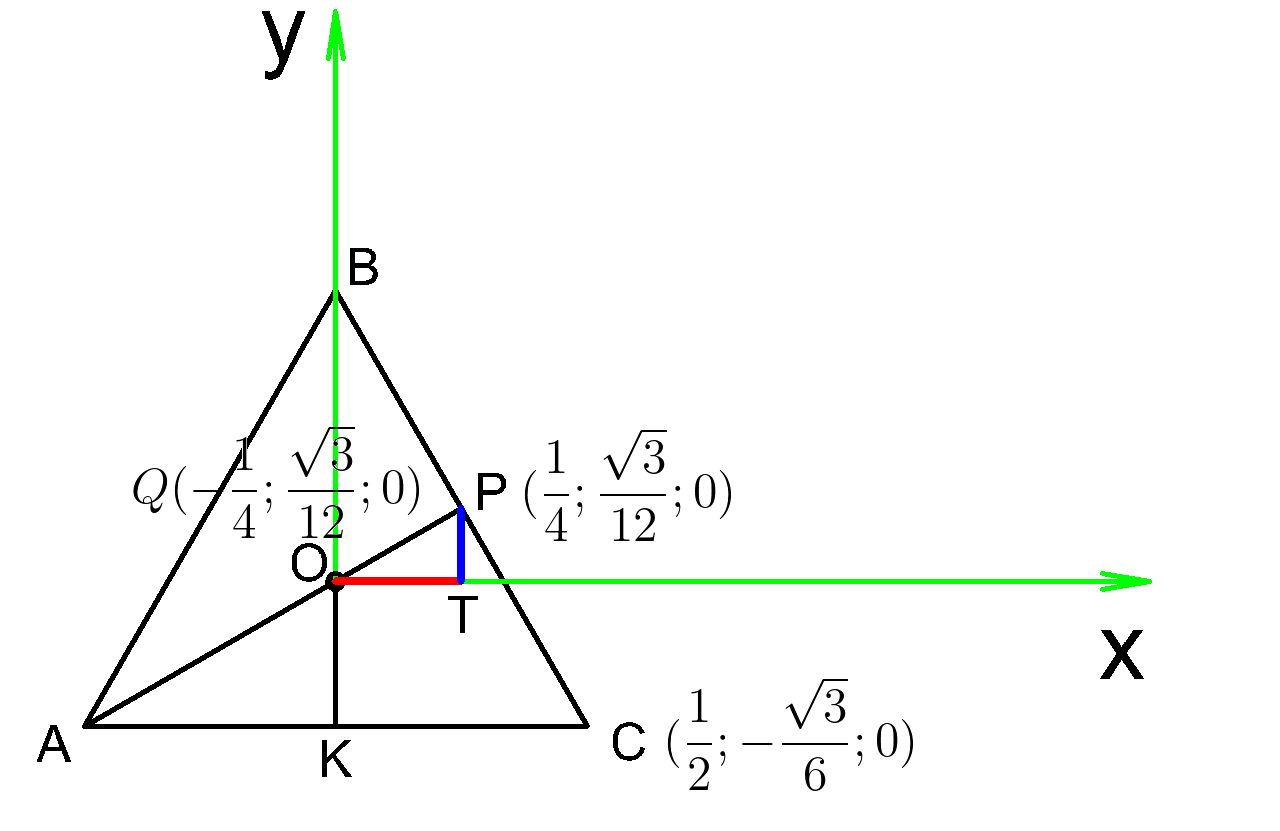
Теперь мы знаем координаты точки \( P(\dfrac{1}{4};\dfrac{\sqrt{3}}{12};0 ) \)
Точка \(Q\) симметрична точке \(P\) относительно оси ординат, поэтому имеет такую же абсциссу, что и точка \(P\), но взятую с обратным знаком.Ординаты этих точек равны.
Абсцисса точки \( C \) численно равна \(KC=\dfrac{1}{2}\), а ее ордината длине отрезка \(OK\), взятая с обратным знаком.

Теперь строим объемный чертеж нашей пирамиды и видим, что вершина \( D \) лежит на оси \( Z \) , поэтому абсцисса и ордината точки \( D \) будут равны нулю, а \( Z \) координата будет равна отрезку \( DO \)

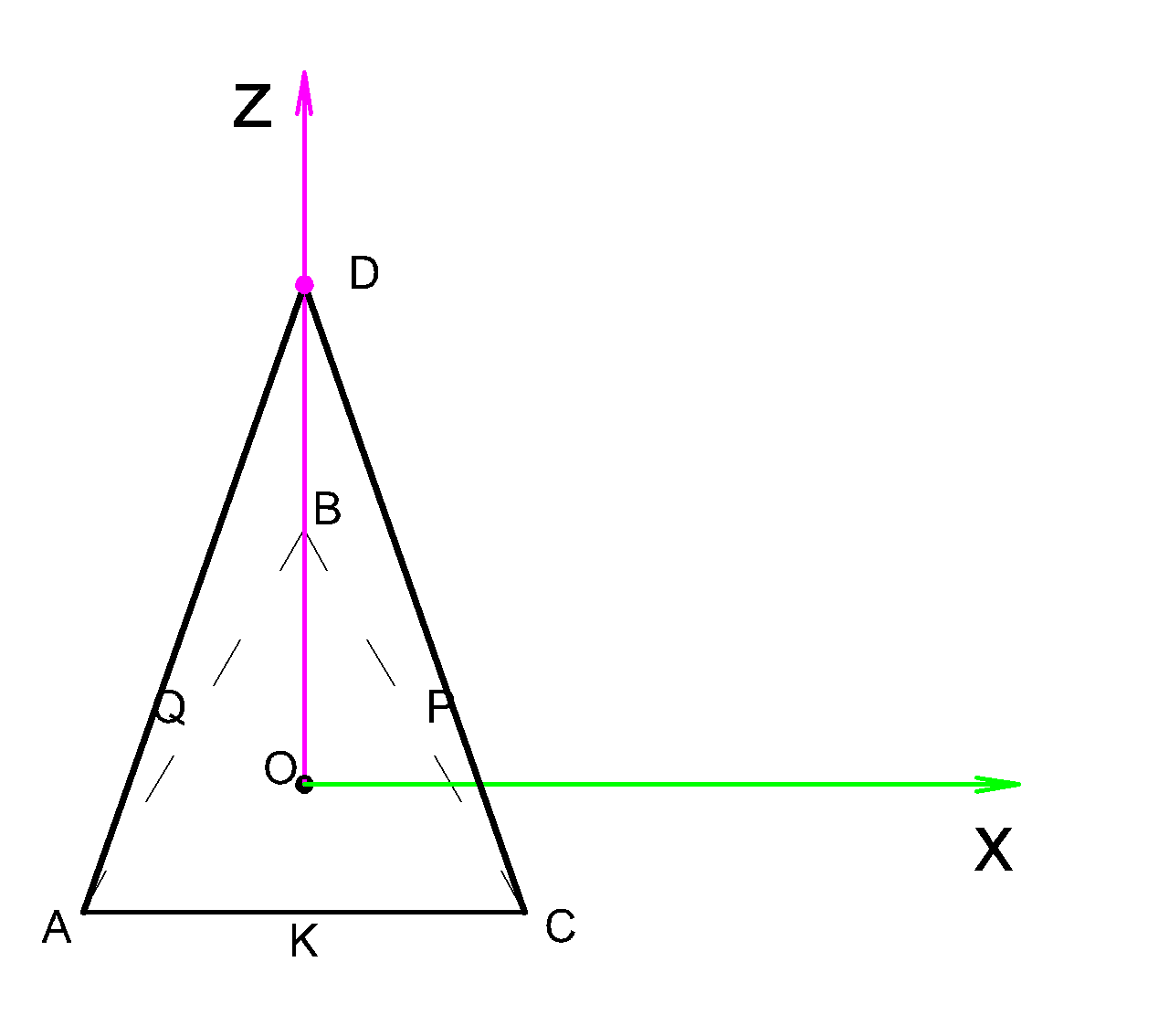
Найдем \( DO \) из треугольника \( DOK: \)
\(DK=BK=\dfrac{\sqrt{3}}{2} \) так как это высоты граней, а все грани одинаковы. \(OK =\dfrac{\sqrt{3}}{6} \)


\(DO= \sqrt{ \left(\dfrac{\sqrt{3}}{2} \right )^2 - \left(\dfrac{\sqrt{3}}{6} \right )^2 } = \dfrac{\sqrt{2}}{\sqrt{3}} \)
Теперь мы знаем координаты точки \( D(0;0;\dfrac{\sqrt{2}}{\sqrt{3}} ) \)
Косинус угла между векторами \( \vec{a}(x_1;y_1;z_1) \ и \ \vec{b}(x_2;y_2;z_2) \) находится по формуле:

\( cos \ \alpha = \dfrac{x_1 \cdot x_2+y_1\cdot y_2 +z_1\cdot z_2 } { \sqrt {x_{1}^2+y_{1}^2+z_{1}^2}\cdot \sqrt {x_{2}^2+y_{2}^2 +z_{2}^2} } \)

---

\( (x_1;y_1;z_1) \) это координаты вектора \( \vec{a} \)
\( (x_2;y_2;z_2) \) это координаты вектора \( \vec{b} \)

Представим какой-то произвольный вектор \( \vec{GM} \)
Точка \( G \{x_1;y_1;z_1 \} \) это начало вектора

Точка \( M \{x_2;y_2;z_2 \} \) это конец вектора
Для нахождения координат вектора нужно из координат конца вектора вычесть координаты начала вектора:

\(\vec{GM} \{x_2-x_1; y_2-y_1 ;z_2-z_1 \} \)
Теперь вернемся к нашим векторам \(\vec{QC} \) и \(\vec{DP} \)
\(\vec{QC} \{ \dfrac{1}{2}-(-\dfrac{1}{4});-\dfrac{\sqrt{3}}{6}-\dfrac{\sqrt{3}}{12};0 \} \)

\(\vec{QC} \{ \dfrac{3}{4};-\dfrac{\sqrt{3}}{4};0 \} \)

\(\vec{DP} \{ \dfrac{1}{4}-0; \dfrac{\sqrt{3}}{12}-0;0-\dfrac{\sqrt{2}}{\sqrt{3}} \} \)

\(\vec{DP} \{ \dfrac{1}{4}; \dfrac{\sqrt{3}}{12};-\dfrac{\sqrt{2}}{\sqrt{3}} \} \)

\( cos \ \alpha = \dfrac{\dfrac{3}{4} \cdot \dfrac{1}{4}+ \left( -\dfrac{\sqrt{3}}{4} \right ) \cdot \dfrac{\sqrt{3}}{12} +0\cdot \left (-\dfrac{\sqrt{2}}{\sqrt{3}} \right )} { \sqrt {\left(\dfrac{3}{4}\right ) ^2+\left( -\dfrac{\sqrt{3}}{4} \right )^2+0^2}\cdot \sqrt {\left(\dfrac{1}{4}\right )^2+\left( \dfrac{\sqrt{3}}{12} \right )^2 +\left(-\dfrac{\sqrt{2}}{\sqrt{3}} \right)^2} } \)
\( cos \ \alpha = \dfrac{\dfrac{3}{16} -\dfrac{3}{48}} { \sqrt {\dfrac{9}{16}+\dfrac{3}{16}}\cdot \sqrt {\dfrac{1}{16}+ \dfrac{3}{144}+\dfrac{2}{3}} } \)


\( cos \ \alpha = \dfrac{\dfrac{1}{8}} { \sqrt {\dfrac{9}{16}+\dfrac{3}{16}}\cdot \sqrt {\dfrac{1}{16}+ \dfrac{3}{144}+\dfrac{2}{3}} } \)


\( cos \ \alpha = \dfrac{\dfrac{1}{8}} { \sqrt {\dfrac{12}{16}}\cdot \sqrt {\dfrac{108}{144}} } \)


\( cos \ \alpha = \dfrac{\dfrac{1}{8}} { \sqrt {\dfrac{3}{4}}\cdot \sqrt {\dfrac{3}{4}} } \)


\( cos \ \alpha = \dfrac{1}{8}:\dfrac{3}{4}=\dfrac{1}{6} \)

\(\alpha =arccos \left (\dfrac{1}{6} \right ) \)