Параллелепипед .

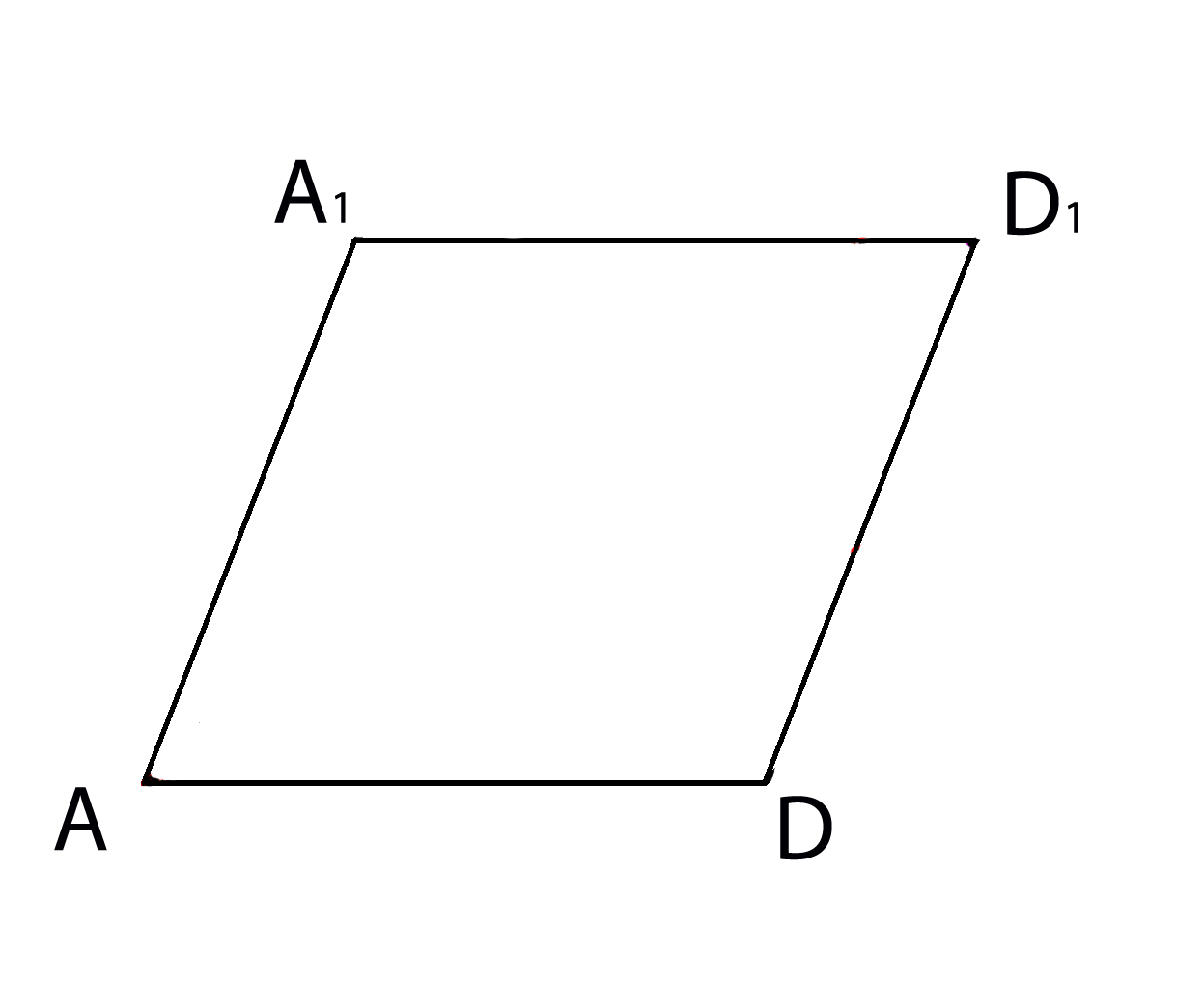
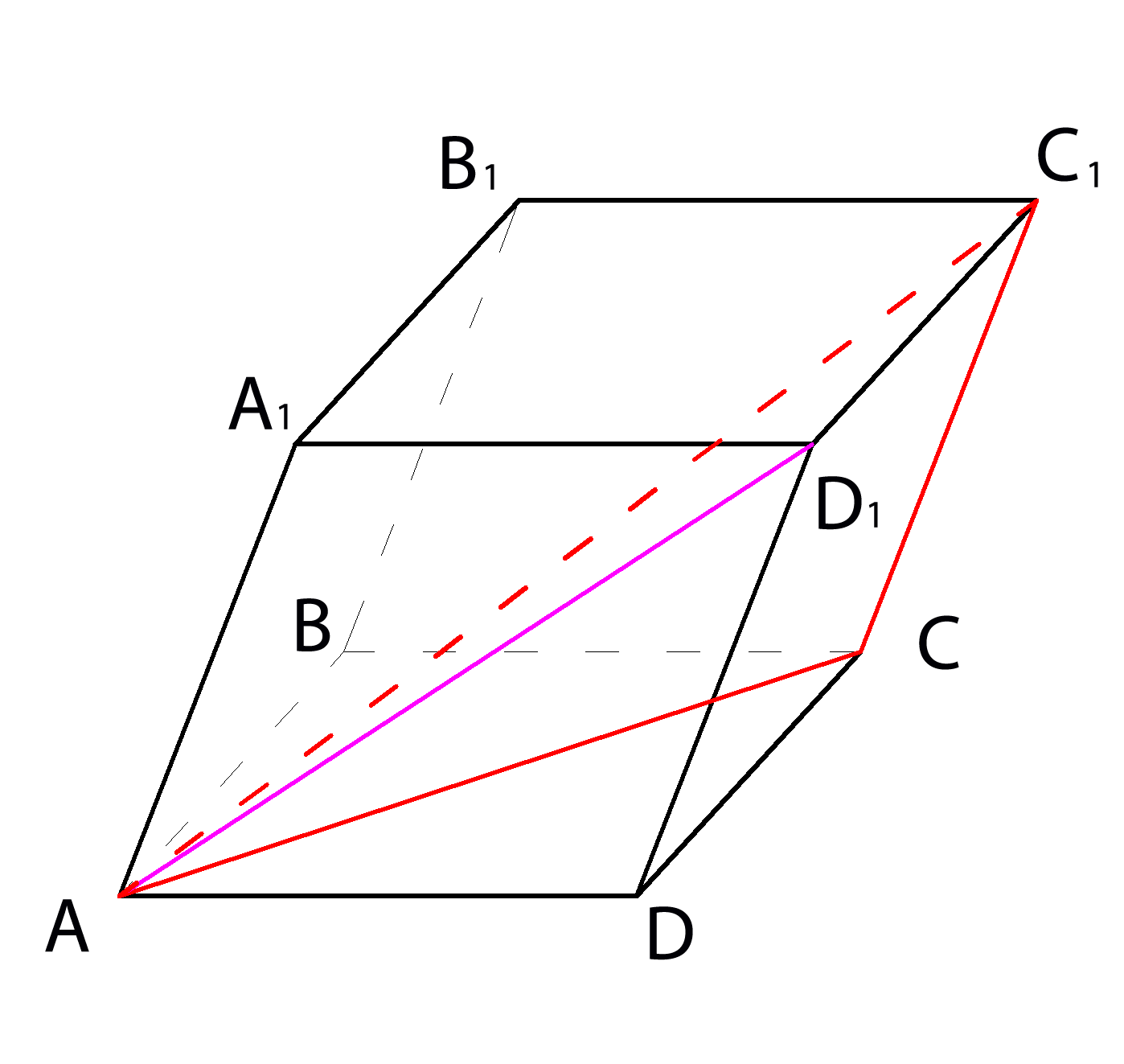
1. В основании наклонного параллелепипеда \(ABCDA_1B_1C_1D_1 \) лежит квадрат \( ABCD \) со стороной \( \sqrt{2} . \) Ребро \( AA_1=\sqrt{8} \) , а угол \( A_1AD=60^0 . \)
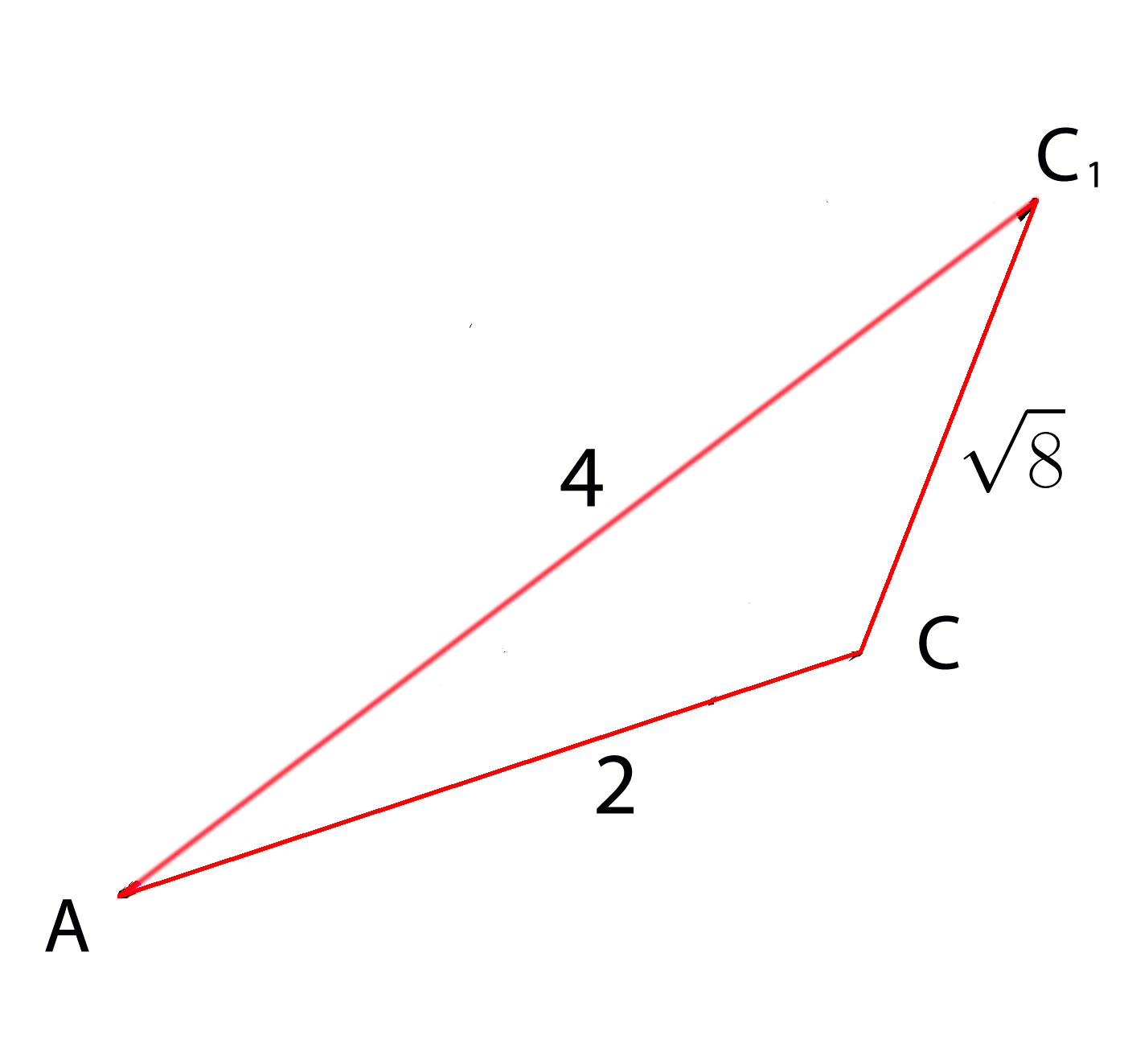
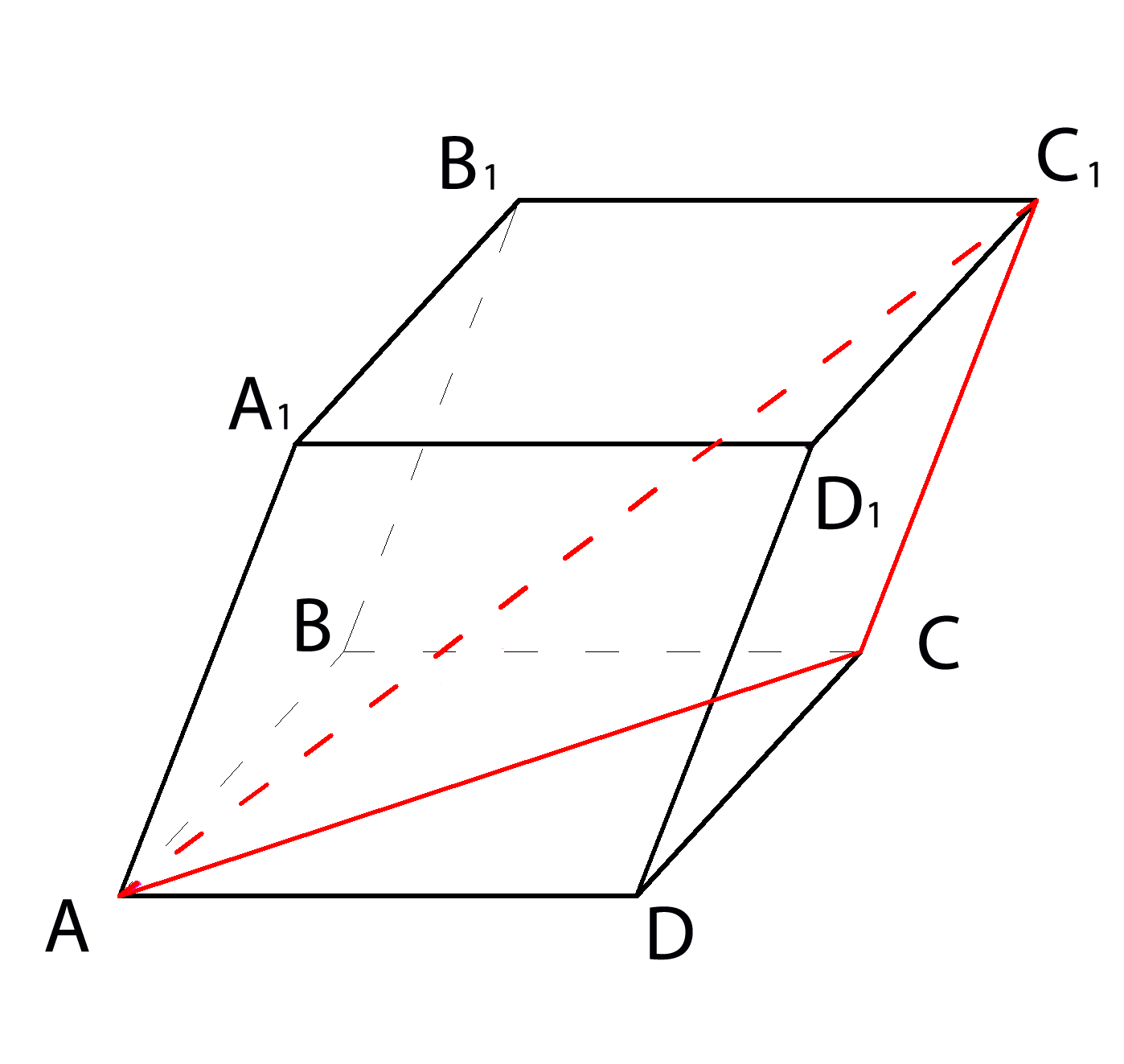
Найдите угол между прямой \( AC \) и прямой \( AC_1 \)
Показать ответ Показать решение Видеорешение

Найдем угол \( ADD_1 \)
Грань \( AA_1D_1D \) является параллелограммом, найдем угол \( D \) если угол \(A=60^0 \)

\( \angle A+\angle D=180^0 \)
\( \angle D=180^0-120^0 \)
\( \angle D=120^0 \)
Проведем отрезок \(AD_1\) и вычислим его по теореме косинусов:

\(AD_1^2=AD^2+DD_1^2-2 \cdot AD \cdot DD_1 \cdot cos \ \angle D \)

\(AD_1^2=\sqrt{2}^2+\sqrt{8}^2-2 \cdot \sqrt{2} \cdot \sqrt{8} \cdot cos \ 120^0 \)

\(AD_1^2=2+8-2 \cdot \sqrt{2} \cdot \sqrt{8} \cdot (-0,5) \)

\(AD_1^2=10-2 \cdot \sqrt{16} \cdot (-0,5) \)

\(AD_1^2=10+2 \cdot 4 \cdot (0,5) \)

\(AD_1=\sqrt{14} \)



Теперь найдем \(AC_1 \) из треугольника \( AD_1C_1 \), угол \( AD_1C_1 \) прямой

\(AC_1=\sqrt{ \sqrt{14}^2 +\sqrt{2}^2 }=4 \)

Теперь найдем \(AC=\sqrt{ \sqrt{2}^2+ \sqrt{2}^2 } =2 \)

Составим теорему косинусов для треугольника \(ACC_1 \)



\(\sqrt{8}=4^2+2^2-2\cdot 4 \cdot 2 \cdot cos \ \angle C_1AC \)

\(8=20-16 cos \ \angle C_1AC \)

\(16 cos \ \angle C_1AC=12 \)

\( cos \ \angle C_1AC=\dfrac{12}{16}=\dfrac{3}{4} \)

\( \angle C_1AC=arccos \left (\dfrac{3}{4} \right) \)

Ответ: \( arccos \left (\dfrac{3}{4} \right) \)