Биссектриса, медиана и высота.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны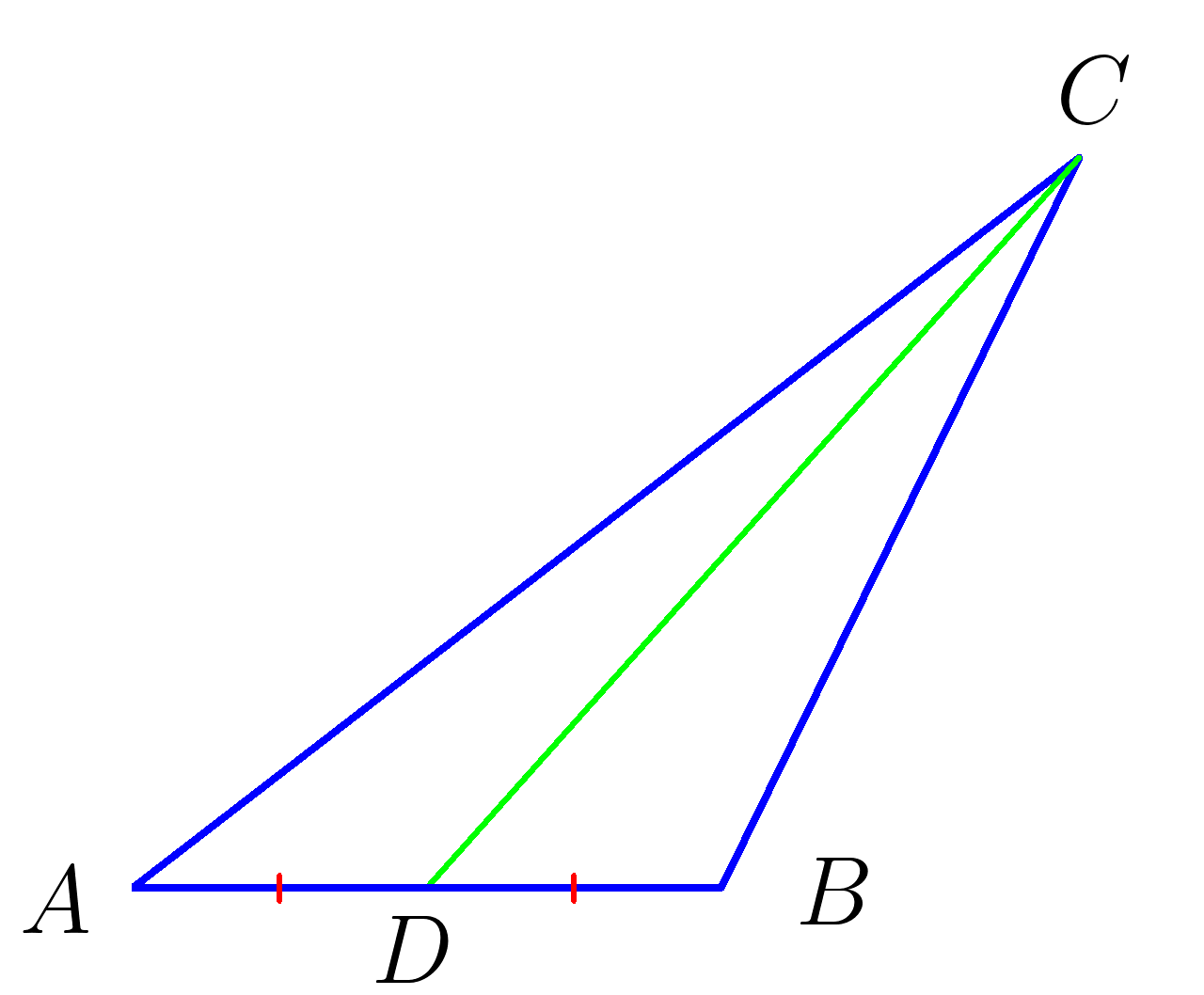

\( AD=BD\)
\(CD- медиана\)

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону

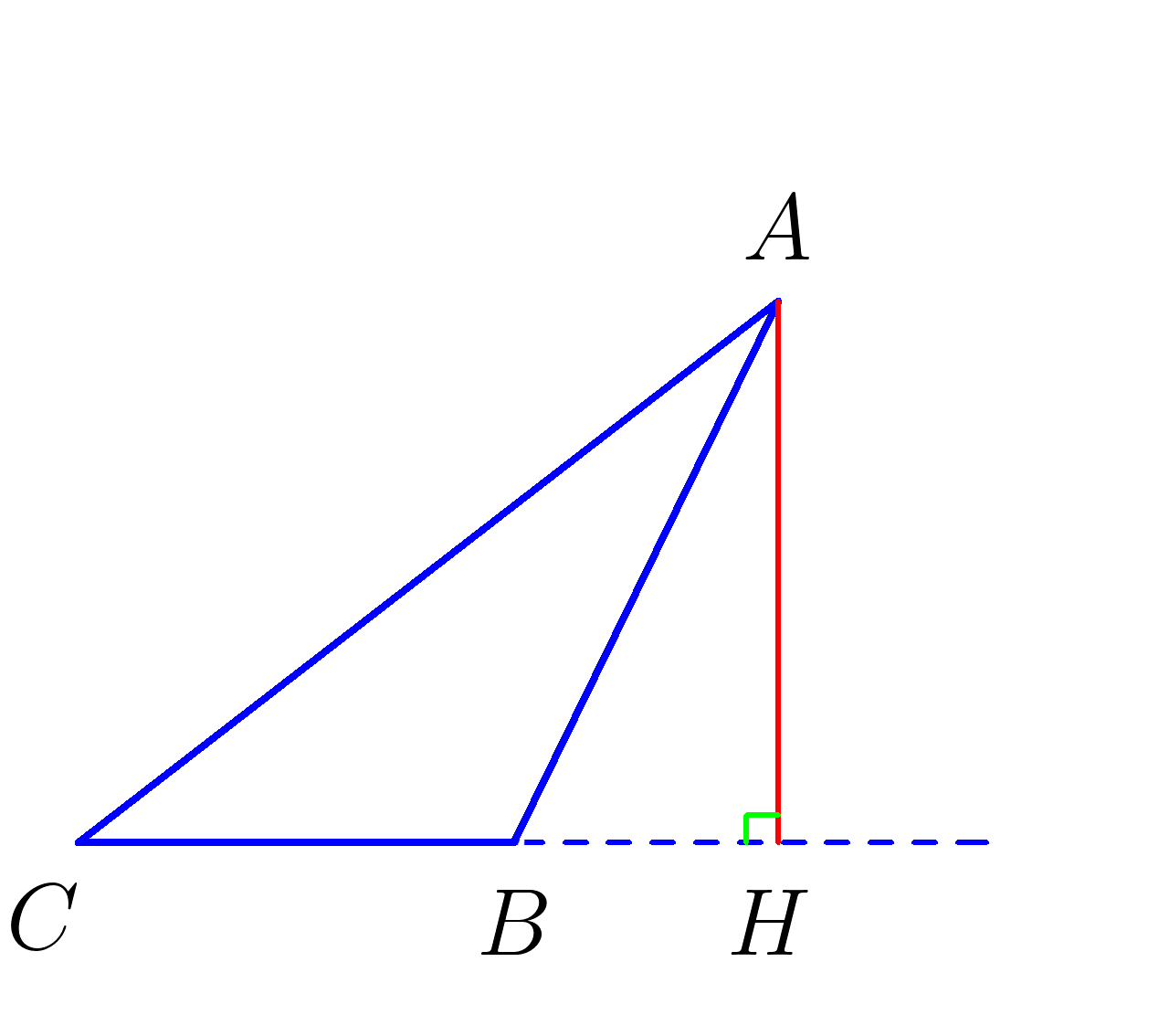
\(AH \) Высота треугольника \( ABC \)

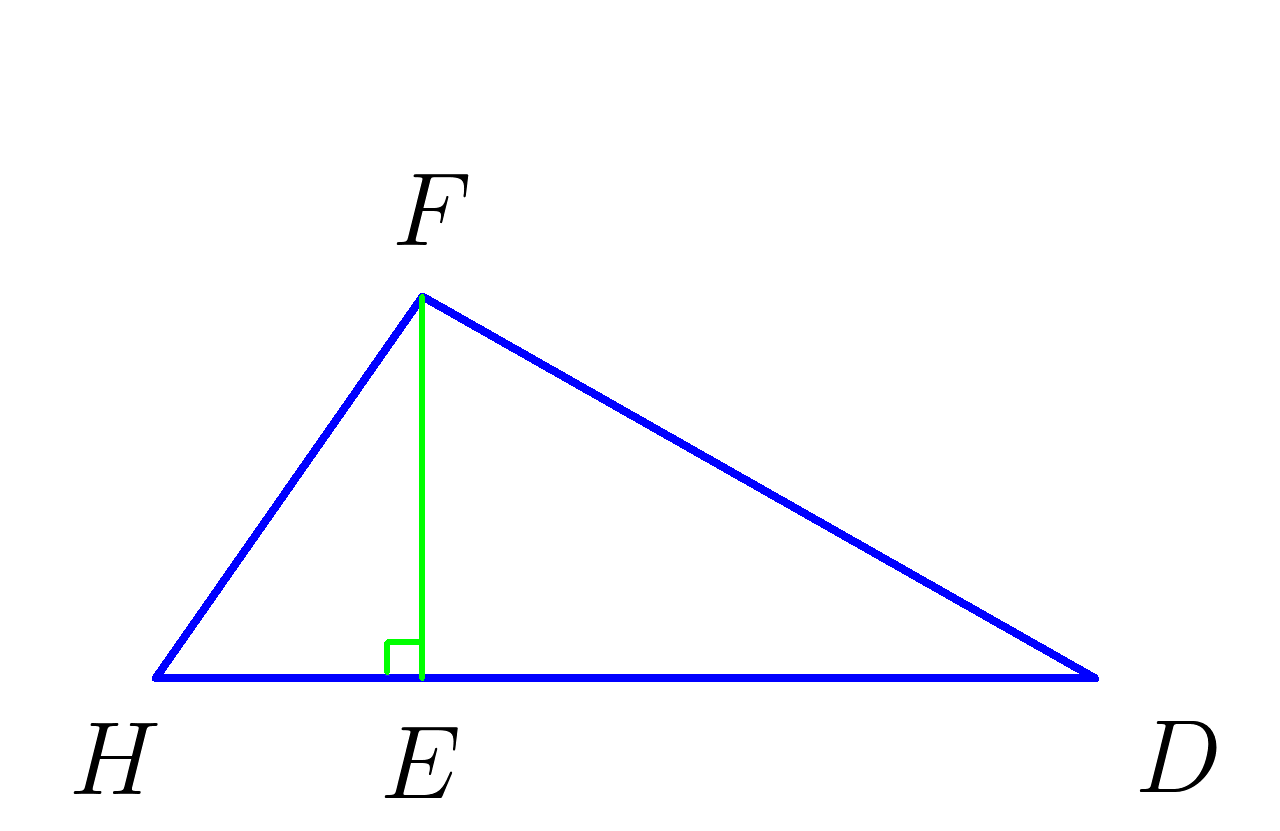
\(FE \) Высота треугольника \( HFD \)

Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой, лежащей на противоположной стороне

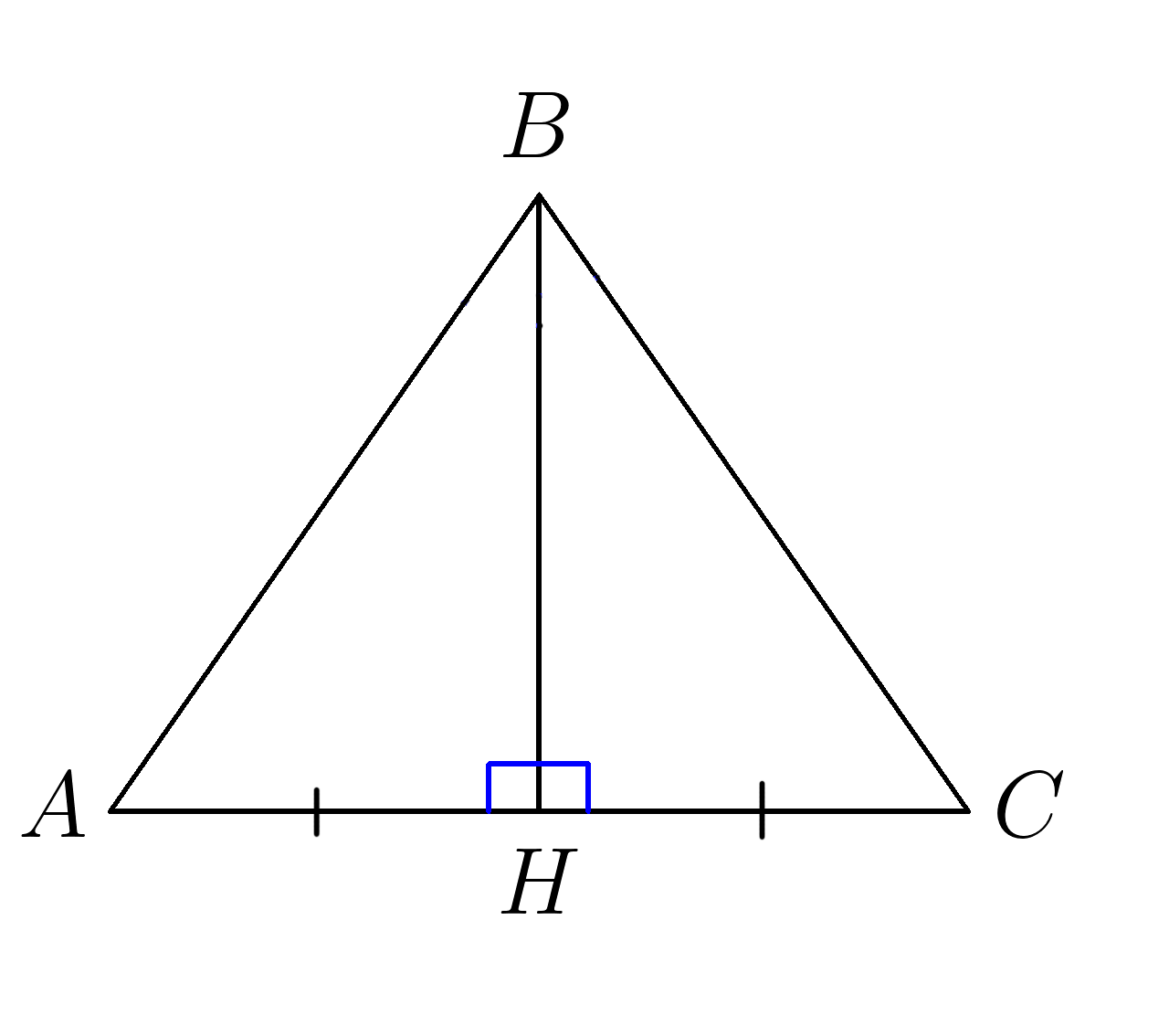
1. В треугольнике \(ABC \:\: BH \) медиана и высота . Доказать равенство треугольников \(ABH \ и \ BHC\).

Показать подсказку Показать решение Видеорешение

\(BH\) общая

Дано: \(BH \) медиана и высота

Доказать: \(ΔABH=ΔBHC\)

Доказательство:

\( 1)\:\: AH=HC \) (так как \(BH\) медиана )
2) \(∡AHB=∡BHC=90^0 \) (так как \(BH\) высота)
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по первому признаку.

ПОЗЖЕ

2. В треугольнике \(ABC \:\: BH \) медиана и высота . \(AB=7. \) Найти \(BC \).

Показать ответ Показать решение Видеорешение

\( BC= 7 \)

Дано: \(BH \) медиана и высота, \(AB=7 \)

Найти: \(BC\)

Сначала докажем равенство треугольников \(ABH \) и \( BHC \) :

\( 1)\:\: AH=HC \) (так как \(BH\) медиана )
2) \(∡AHB=∡BHC=90^0 \) (так как \(BH\) высота)
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по первому признаку.

В равных треугольниках против равных углов лежат равные стороны

\(AB \) лежит против \( ∡AHB \) , \(BC \) лежит против \( ∡BHC \) \( ∡AHB= ∡BHC \Rightarrow BC= AB=7 \)

Ответ: \( BC= 7 \)

ПОЗЖЕ