Биссектриса
Биссектриса это луч, исходящий из вершины угла и делящий этот угол на два равных угла.
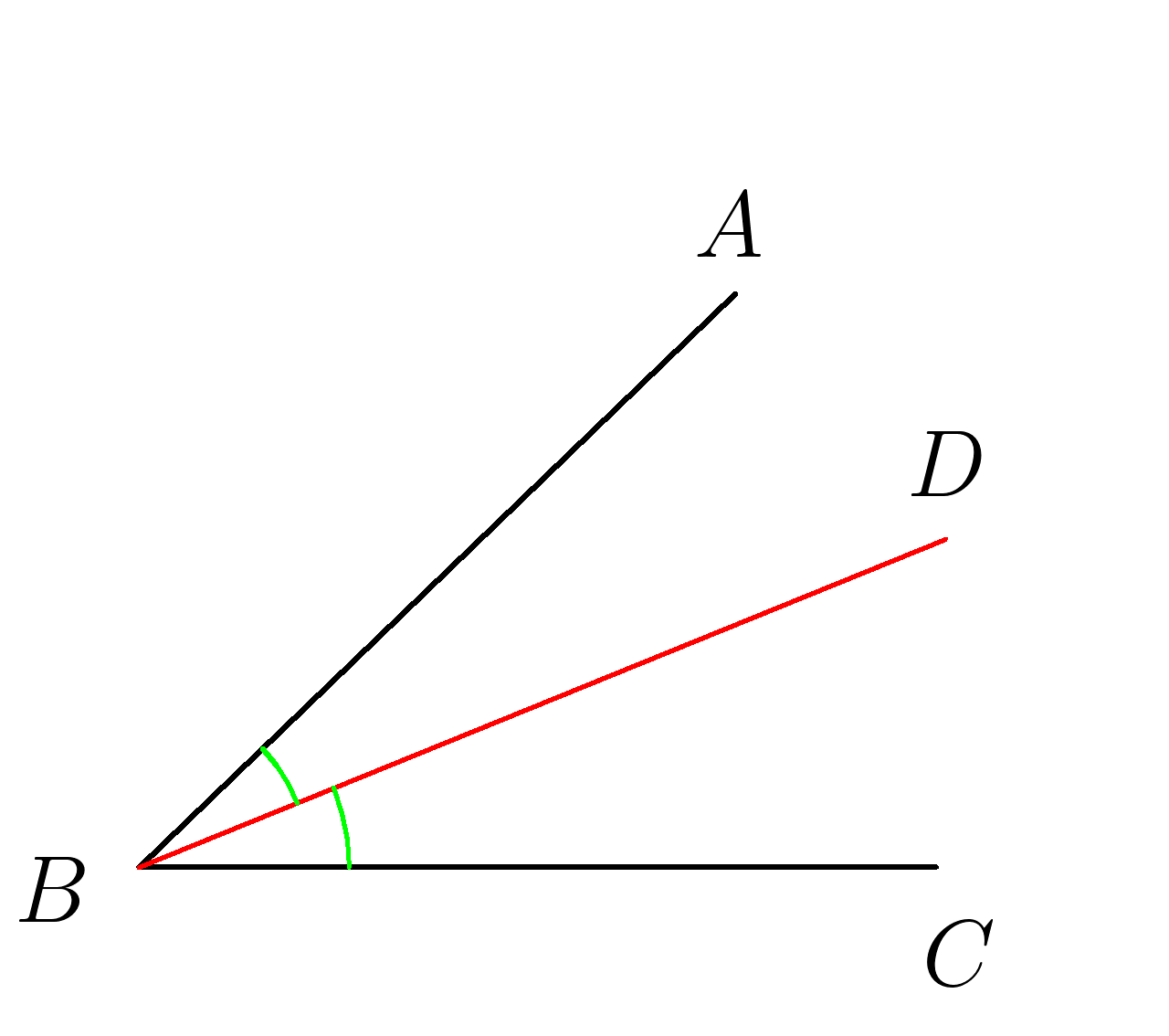
\(BD \) биссектриса угла \( ABC \)
\( \:\:∡ABD=∡DBC\)
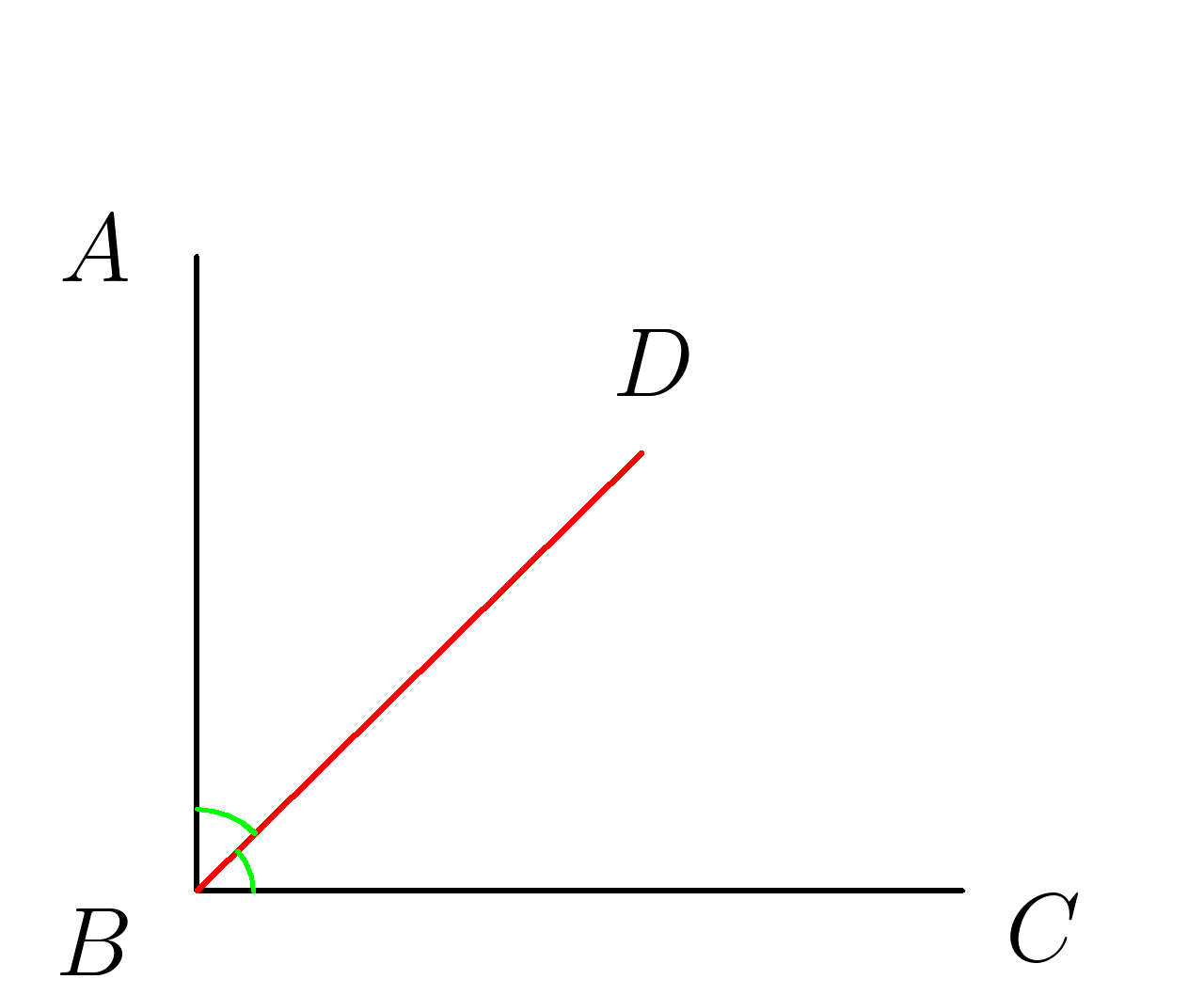
1. Угол \(ABC\) прямой. \(BD\)- его биссектриса. Найти градусную меру угла \(ABD\)
Показать подсказку Показать решение Видеорешение
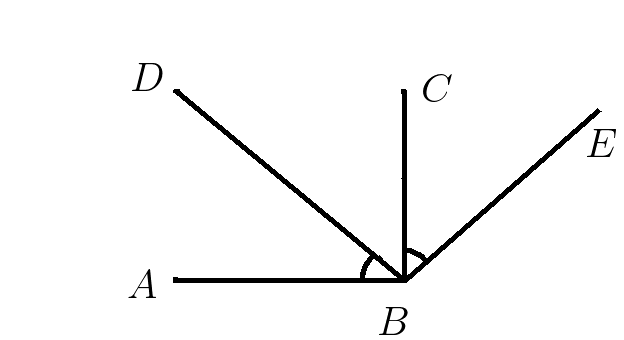
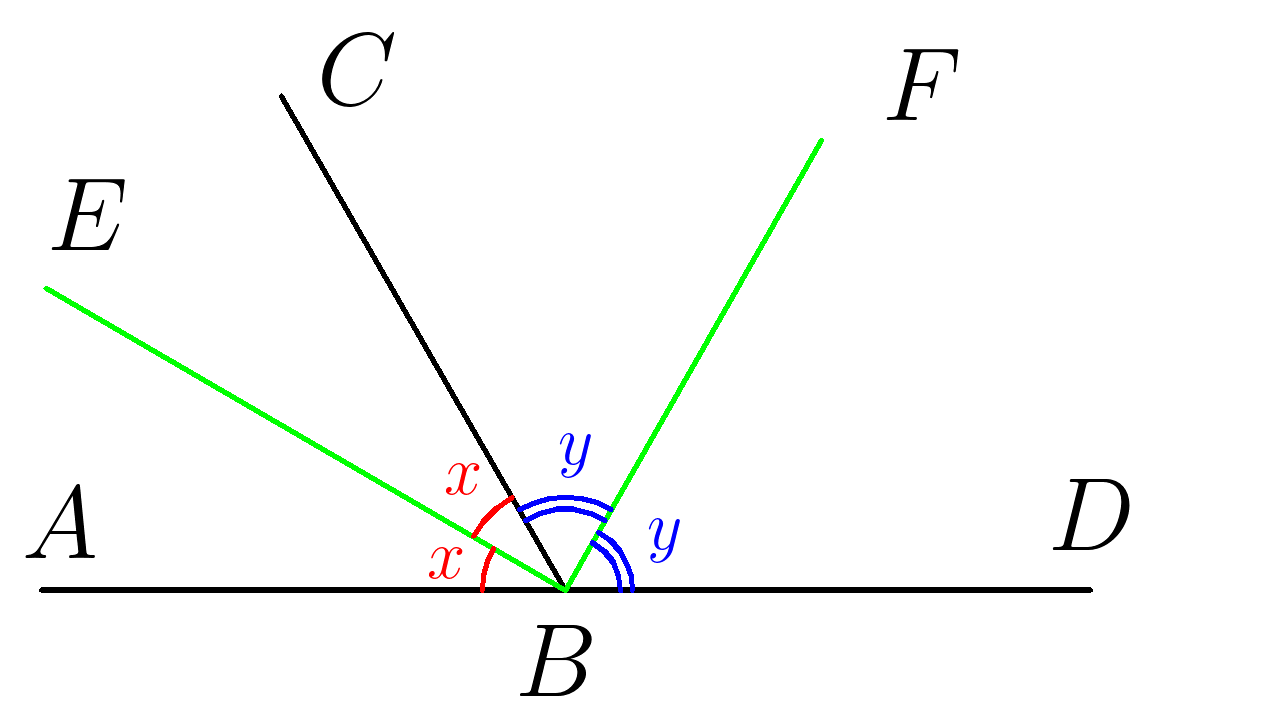
2. На рисунке угол \(ABD\) равен углу \(CBE \) . \(DB\)-биссектриса угла \(ABC\). Найти угол \(ABE\) , если угол \(ABC\) прямой.
Показать ответ Показать решение Видеорешение
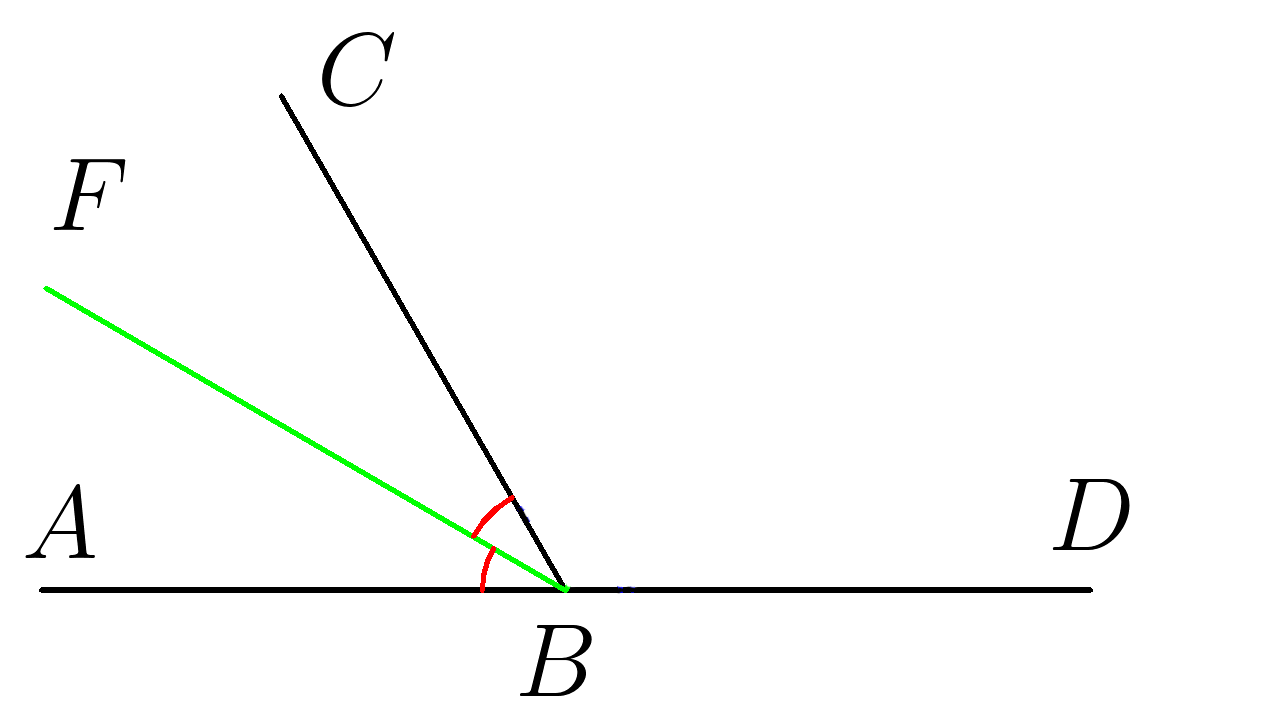
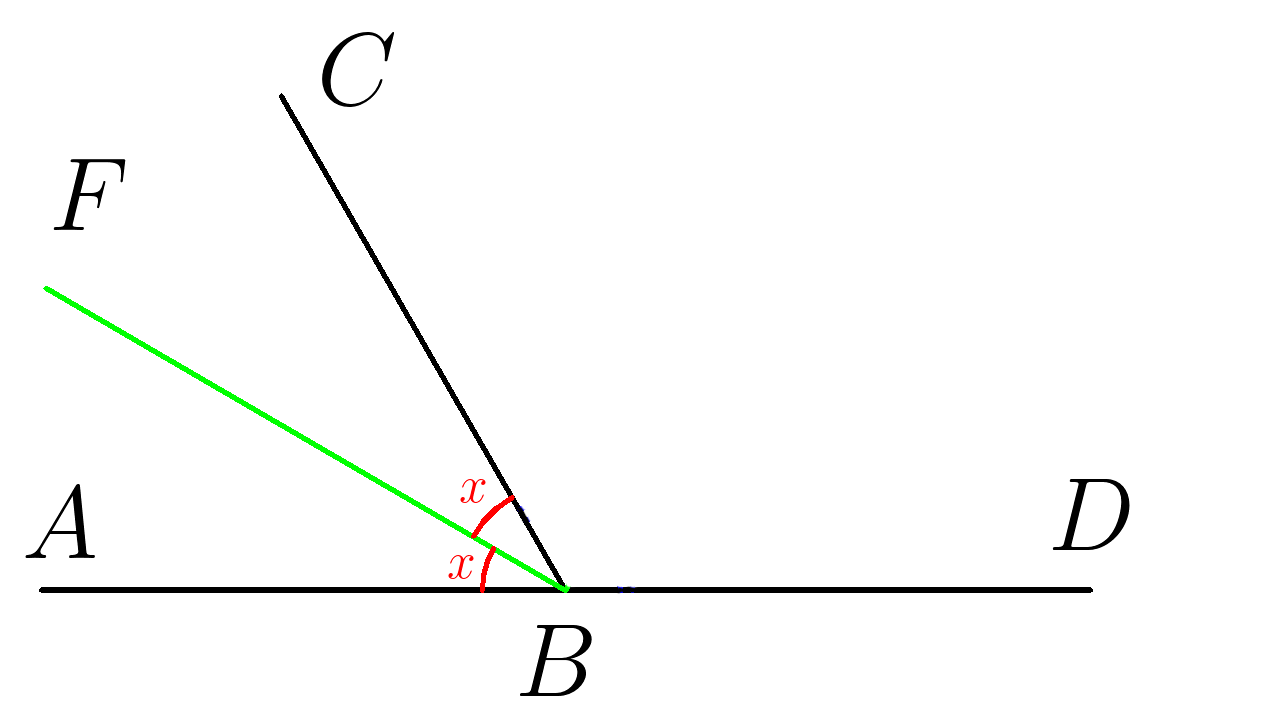
3. \( ∡CBF=25^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение

4. \( ∡CBF=30^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение

5. \( ∡CBF=30^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение

6. \( ∡CBF=35^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение

7. \( ∡FBD=140^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение
Эта же задача с другим решением (для старшеклассников):

7. \( ∡FBD=140^0\) \(BF\)- биссектриса угла \( CBA \). Найти градусную меру угла \(CBD\)
Показать ответ Показать решение Видеорешение
10. Найти угол, образованный биссектрисами двух смежных углов
Показать ответ Показать решение Видеорешение
11. Найти угол, образованный биссектрисами двух вертикальных углов
Показать ответ Показать решение Видеорешение