Первый признак равенства треугольников

Репетитор
по физике

916 478 1032

Репетитор
по алгебре

916 478 1032

Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны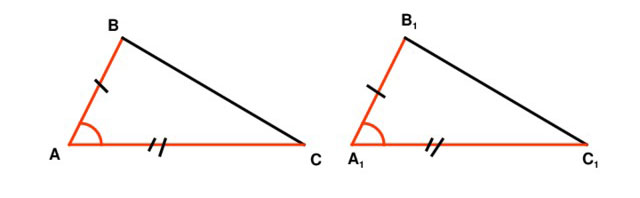
Первый признак равенства треугольников

1) A B = A_{1} B_{1}

2) A C = A_{1} C_{1}

3) ∡ A = ∡ A_{1}

\Rightarrow Δ A B C = Δ A_{1} B_{1} C_{1}

по первому признаку.

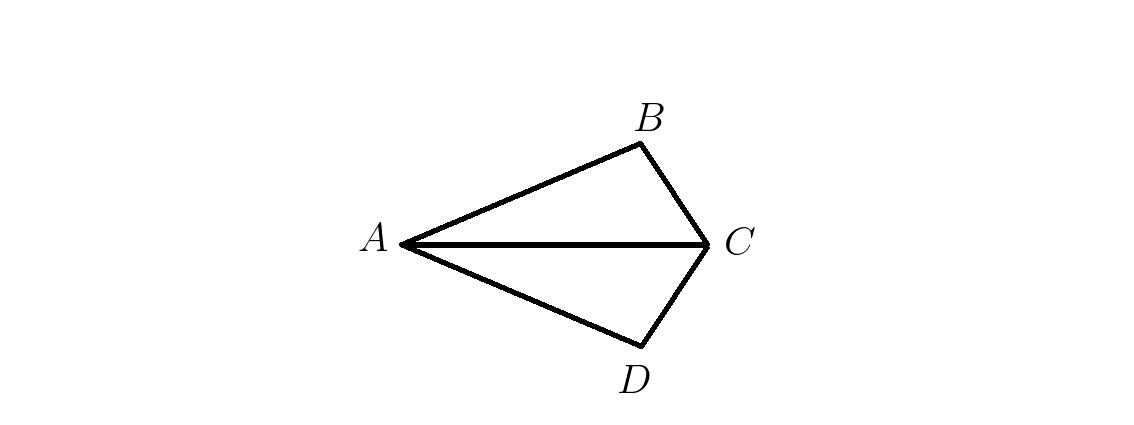
1. В треугольниках $A B C и A C D A B = A D и ∡ B A C = ∡ C A D$ . Доказать равенство треугольников $A B C и A C D$ .

Показать подсказку Показать решение Видеорешение

$A C$ общая

Дано: $A B = A D, ∡ B A C = ∡ C A D$

Доказать: $A B C = A C D$

Доказательство:

$1) A B = A D$ (по условию)
2) $∡ B A C = ∡ C A D (п о у с л о в и ю)$
3) $A C$ общая
$\Rightarrow Δ A B C = Δ A C D$ по первому признаку.

ПОЗЖЕ

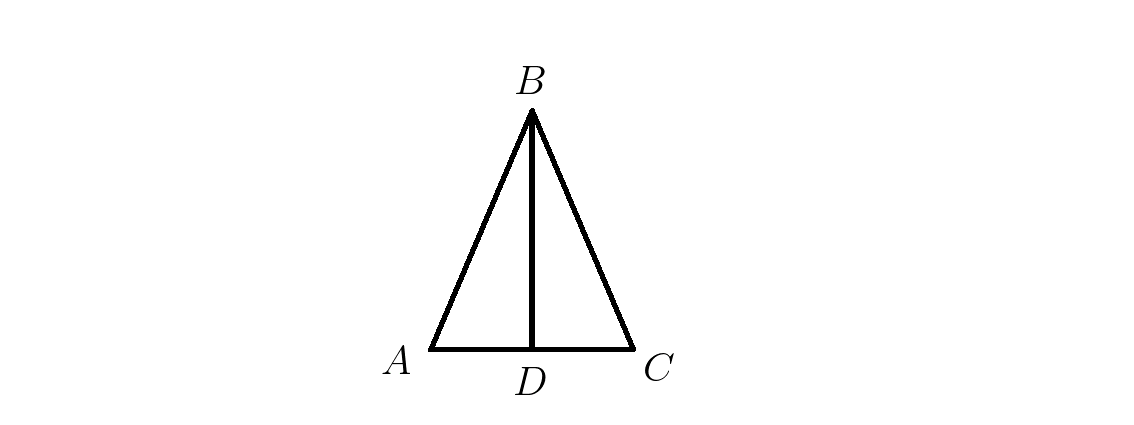
2. В треугольниках $A B D и B C D A B = B C и ∡ A B D = ∡ C B D$ . Доказать равенство треугольников $A B D и B C D$ .

Показать подсказку Показать решение Видеорешение

$B D$ общая

Дано: $A B = B C$ , $∡ A B D = ∡ C B D$
Доказать: $Δ A B D = Δ B C D$

Доказательство:

1) $A B = B C$ (по условию)
2) $∡ A B D = ∡ C B D$ (по условию)
3) $B D$ общая
$\Rightarrow Δ A B D = Δ B C D$ по первому признаку.

ПОЗЖЕ

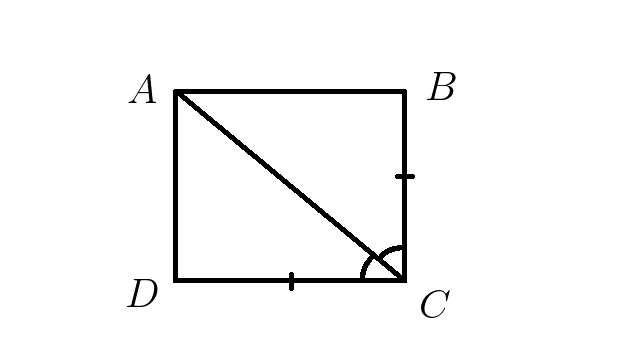
3. В треугольниках $A B C и A C D B C = D C и ∡ B C A = ∡ A C D$ . Доказать равенство треугольников $A B C и A C D$ .

Показать подсказку Показать решение Видеорешение

$A C$ общая

Дано: $B C = D C$ , $∡ B C A = ∡ A C D$
Доказать: $Δ A B C = Δ A C D$

Доказательство:

1) $B C = D C$ (по условию)
2) $∡ B C A = ∡ A C D$ (по условию)
3) $A C$ общая
$\Rightarrow Δ A B C = Δ A C D$ по первому признаку.

ПОЗЖЕ

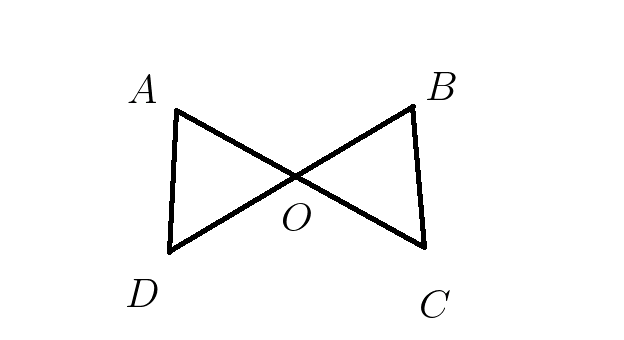
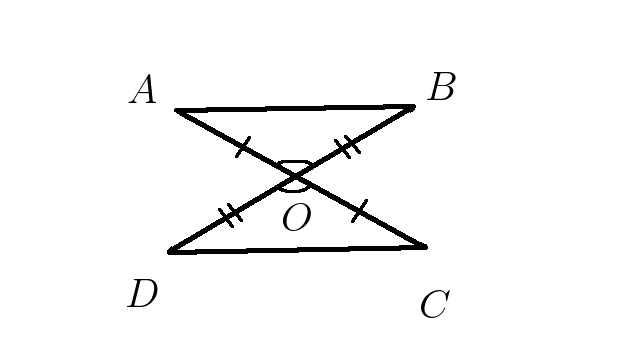
4. В треугольниках $A O D и B O C A O = O C и D O = O B$ . Доказать равенство треугольников $A O D и B O C$ .

Показать подсказку Показать решение Видеорешение

$∡ A O D = ∡ B O C$ так как это вертикальные углы.

Дано: $A O = O C$ , $D O = O B$
Доказать: $Δ A O D = Δ B O C$

Доказательство:

1) $A O = O C$ (по условию)
2) $D O = O B$ (по условию)
3) $∡ A O D = ∡ B O C$ так как это вертикальные углы.
$\Rightarrow Δ A O D = Δ B O C$ по первому признаку.

ПОЗЖЕ

5. Отрезки $A C и B D$ точкой пересечения $O$ делятся пополам, доказать равенство треугольников $A O B и D O C$

Показать подсказку Показать решение Видеорешение

$∡ A O B = ∡ D O C$ так как это вертикальные углы.

Дано: точка $O$ - середина $A C и B D$
Доказать: $Δ A O B = Δ C O D$

Доказательство:

1) $A O = O C$ (так как точка $O$ середина $A C$ )
2) $D O = O B$ (так как точка $O$ середина $B D$ )
3) $∡ A O B = ∡ D O C$ так как это вертикальные углы.
$\Rightarrow Δ A O B = Δ D O C$ по первому признаку.

ПОЗЖЕ