Третий признак равенства треугольников

Репетитор
по физике

916 478 1032

Репетитор
по алгебре

916 478 1032

Третий признак равенства треугольников

Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны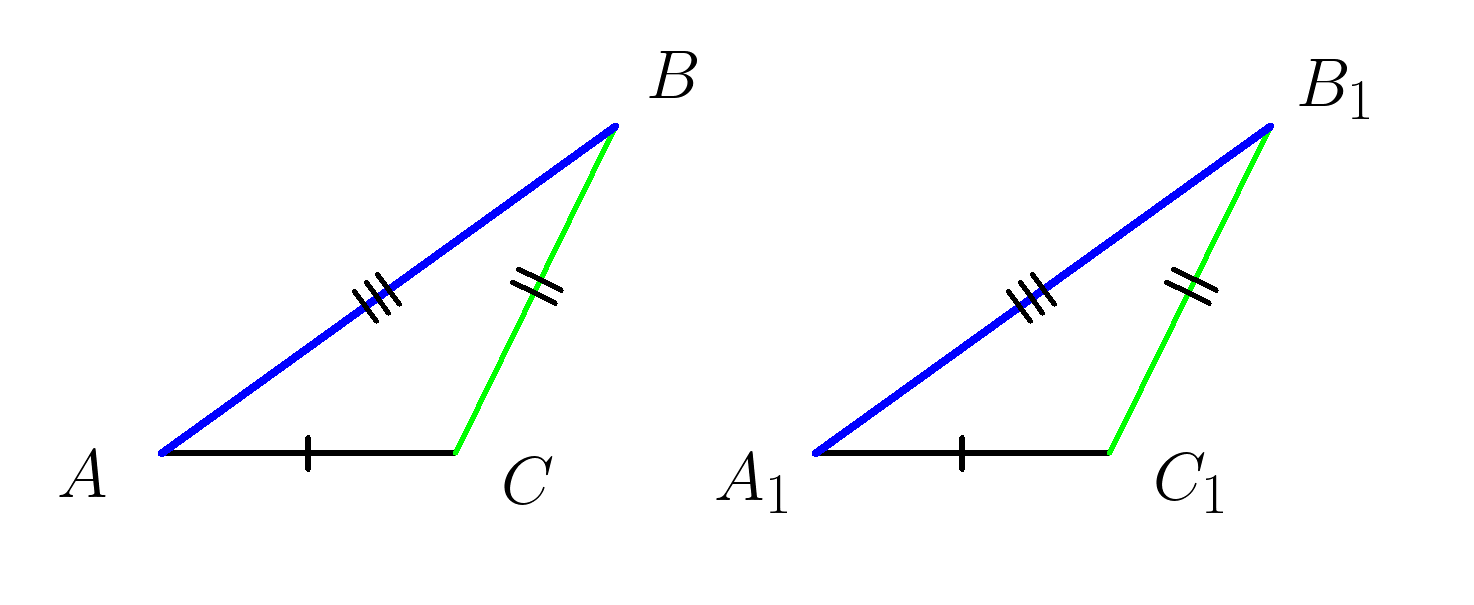
Третий признак равенства треугольников

1) A C = A_{1} C_{1}

2) A B = A_{1} B_{1}

3) B C = B_{1} C_{1}

\Rightarrow Δ A B C = Δ A_{1} B_{1} C_{1}

по третьему признаку.

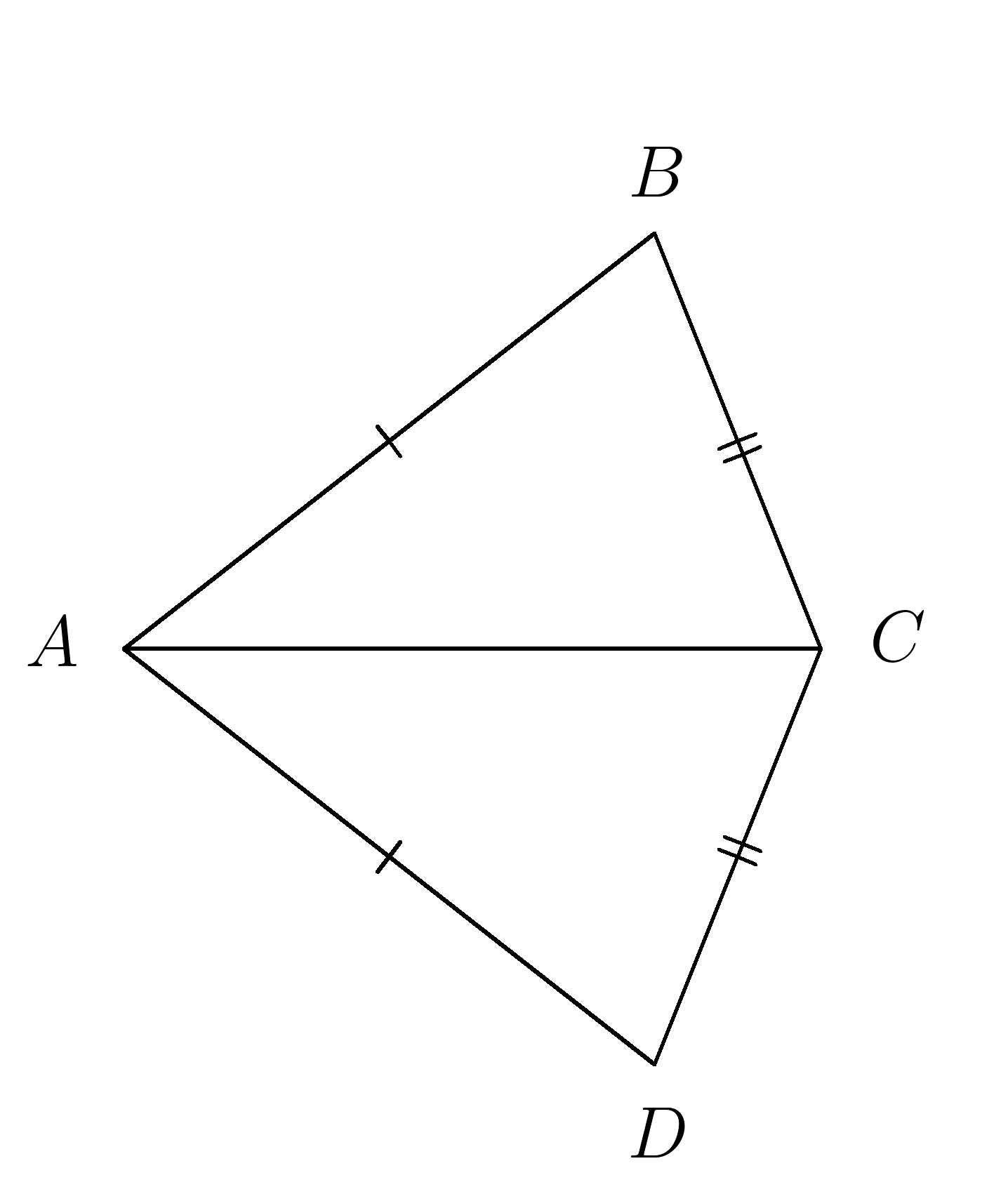
1. На рисунке $A B = A D, B C = C D$ .
Доказать: $Δ A B C = Δ A C D$

Показать подсказку Показать решение Видеорешение

$A C$ общая

Дано: $A B = A D, B C = C D$ .

Доказать: $Δ A B C = Δ A C D$

Доказательство:

$1) A B = A D$ (по условию)
2) $B C = C D$ (по условию)
3) $A C$ общая
$\Rightarrow Δ A B C = Δ A C D$ по третьему признаку.

ПОЗЖЕ

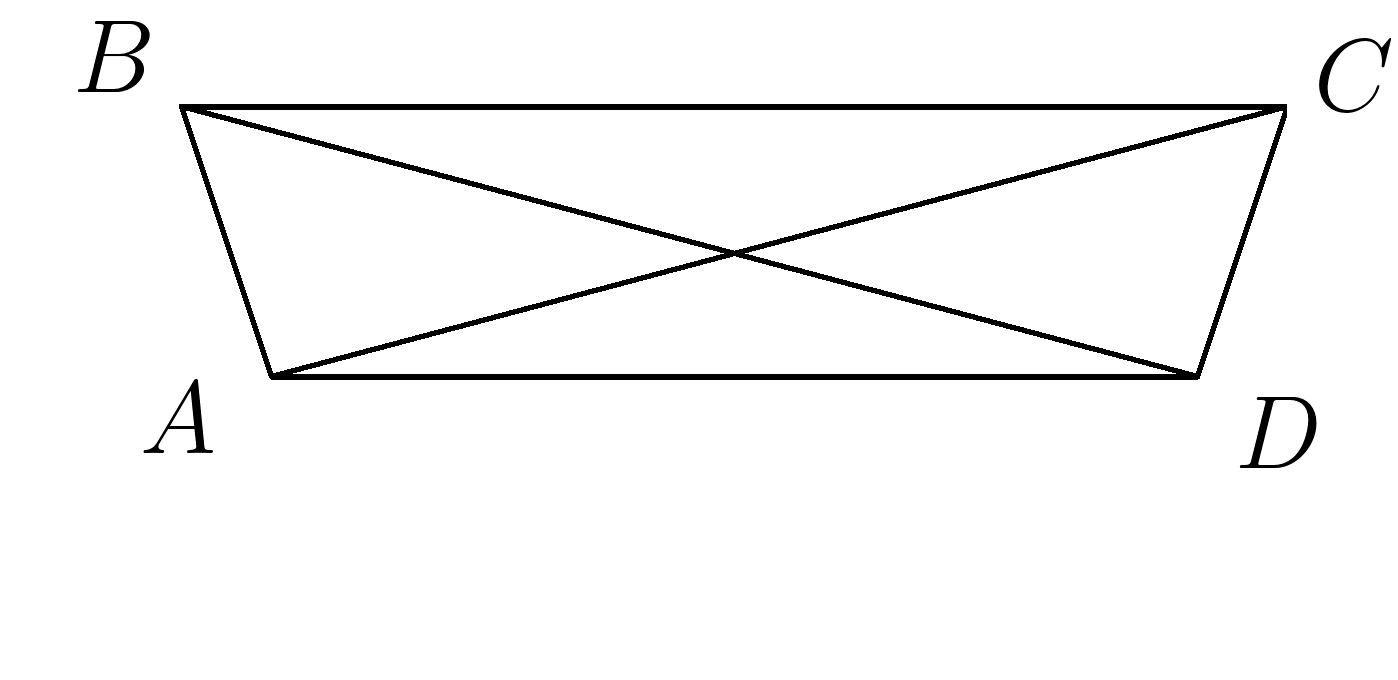
2. На рисунке $A C = B D, A B = C D$ .
Доказать: $Δ A B D = Δ A C D$

Показать подсказку Показать решение Видеорешение

$A D$ общая

Дано: $A C = B D, A B = C D$ .

Доказать: $Δ A B D = Δ A C D$

Доказательство:

$1) A C = B D$ (по условию)
2) $A B = C D$ (по условию)
3) $A D$ общая
$\Rightarrow Δ A B D = Δ A C D$ по третьему признаку.

ПОЗЖЕ

3. На рисунке $A C = B D, A B = C D$ .
Доказать: $Δ A B C = Δ B C D$

Показать подсказку Показать решение Видеорешение

$B C$ общая

Дано: $A C = B D, A B = C D$ .

Доказать: $Δ A B C = Δ B C D$

Доказательство:

$1) A C = B D$ (по условию)
2) $A B = C D$ (по условию)
3) $B C$ общая
$\Rightarrow Δ A B C = Δ B C D$ по третьему признаку.

ПОЗЖЕ

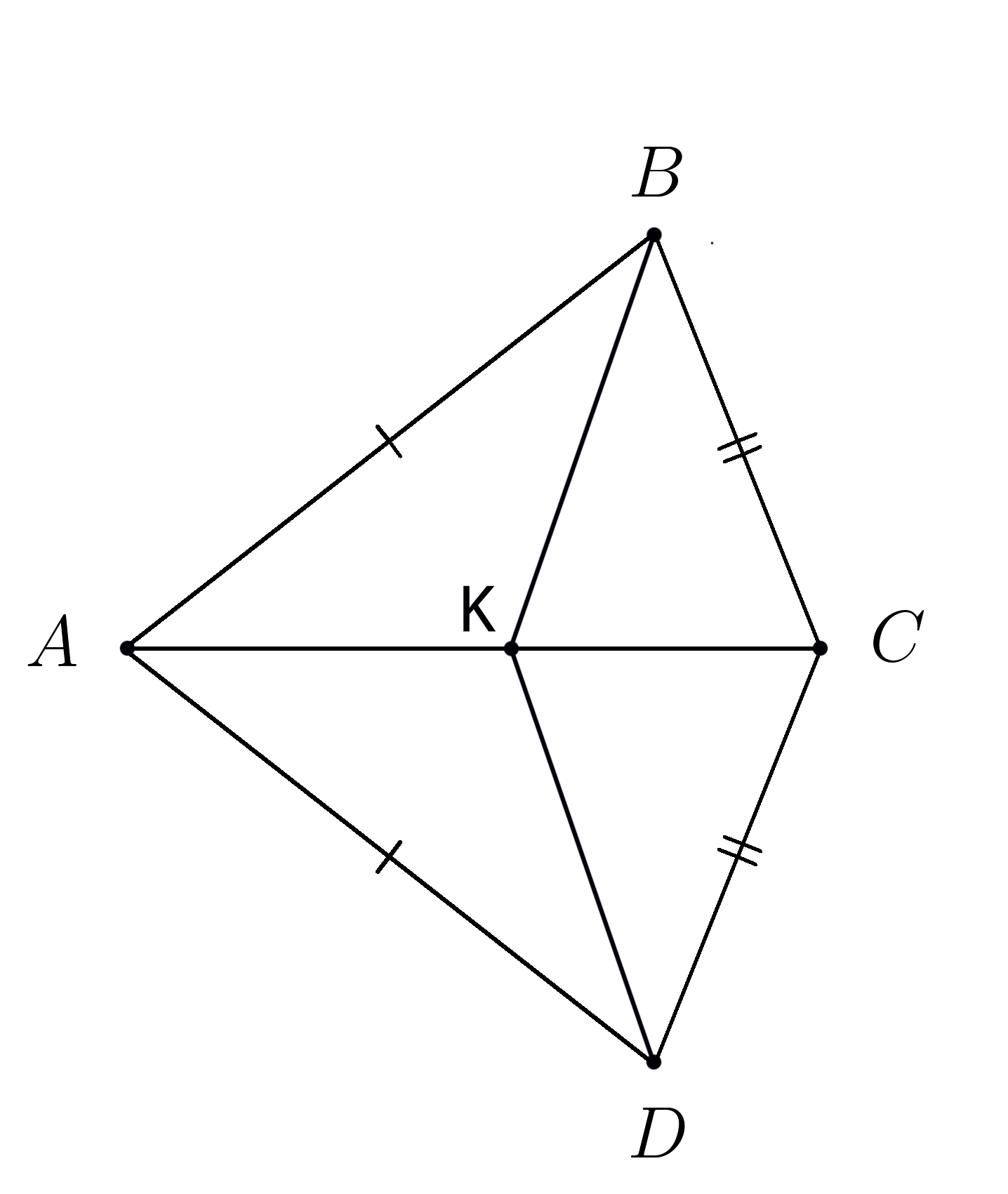
4. На рисунке $A B = A D, B C = C D$ .
На диагонали $A C$ четырехугольника $A B C D$ взята точка $K .$
Доказать: $Δ A B K = Δ A D K$

Показать подсказку Показать решение Видеорешение

Сначала докажем, что $Δ A B C = Δ A C D$

Дано: $A B = A D, B C = C D$ .

Доказать: $Δ A B K = Δ A D K$

Доказательство:

$1) A B = A D$ (по условию)
2) $B C = C D$ (по условию)
3) $A C$ общая
$\Rightarrow Δ A B C = Δ A C D$ по третьему признаку.

$1) ∠ B A K = ∠ D A K$ так как $Δ A B C = Δ A C D$
$2) A B = A D$ (по условию)
$3) A K$ Общая
$\Rightarrow Δ A B K = Δ A D K$ по первому признаку.
Из равенства треугольников $Δ A B K и Δ A D K$ следует равенство их сторон $B K и K D$
Так как в равных треугольниках против равных углов лежат равные стороны.

ПОЗЖЕ