Второй признак равенства треугольников

Репетитор
по физике

916 478 1032

Репетитор
по алгебре

916 478 1032

Второй признак равенства треугольников

Если сторона и прилегающие к ней углы одного треугольника соответственно равна стороне и прилегающим к ней углам другого треугольника другого треугольника, то такие треугольники равны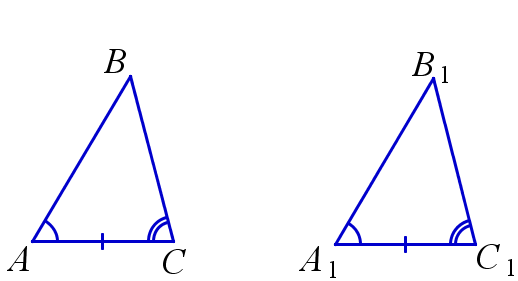
Второй признак равенства треугольников

\( 1)\:\:AC=A_1C_1\)
\( 2)\:\:∡A=∡A_1\)
\( 3)\:\:∡C=∡C_1\)
\(\Rightarrow ΔABC=ΔA_1B_1C_1\) по второму признаку.

1. В треугольниках \(ABH и BHC \:\: ∡ABH=∡HBC и ∡AHB=∡BHC\) . Доказать равенство треугольников \(ABH и BHC\).

Показать подсказку Показать решение Видеорешение

\(BH\) общая

Дано: \(∡AHB=∡BHC , \: ∡ABH=∡HBC\)

Доказать: \(ΔABH=ΔBHC\)

Доказательство:

\( 1)\:\: ∡AHB=∡BHC \) (по условию)
2) \(∡ABH=∡HBC (по условию) \)
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по второму признаку.

ПОЗЖЕ

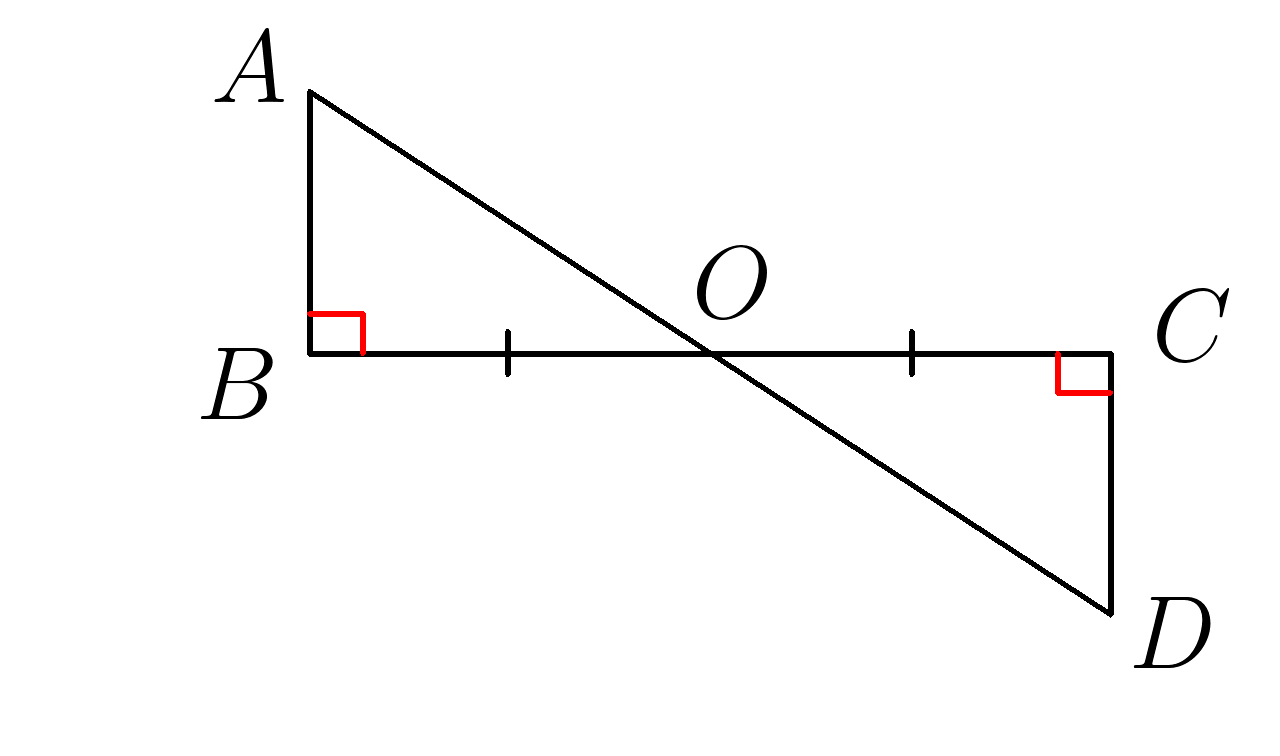
2. \( BO=OC \:\: ∡ABO=∡OCD \) . Доказать равенство треугольников \(ABO и COD\).

Показать подсказку Показать решение Видеорешение

\( ∡AOB=∡COD \) (Так как они вертикальные)

Дано: \(BO=OC , \: ∡ABO=∡OCD\)

Доказать: \( ΔABO = ΔCOD \)

Доказательство:

\( 1)\:\: BO=OC \) (по условию)
2) \( ∡ABO=∡OCD \) (по условию)
3) \( ∡AOB=∡COD \) (Так как они вертикальные)
\(\Rightarrow ΔABO = ΔCOD\) по второму признаку.

ПОЗЖЕ

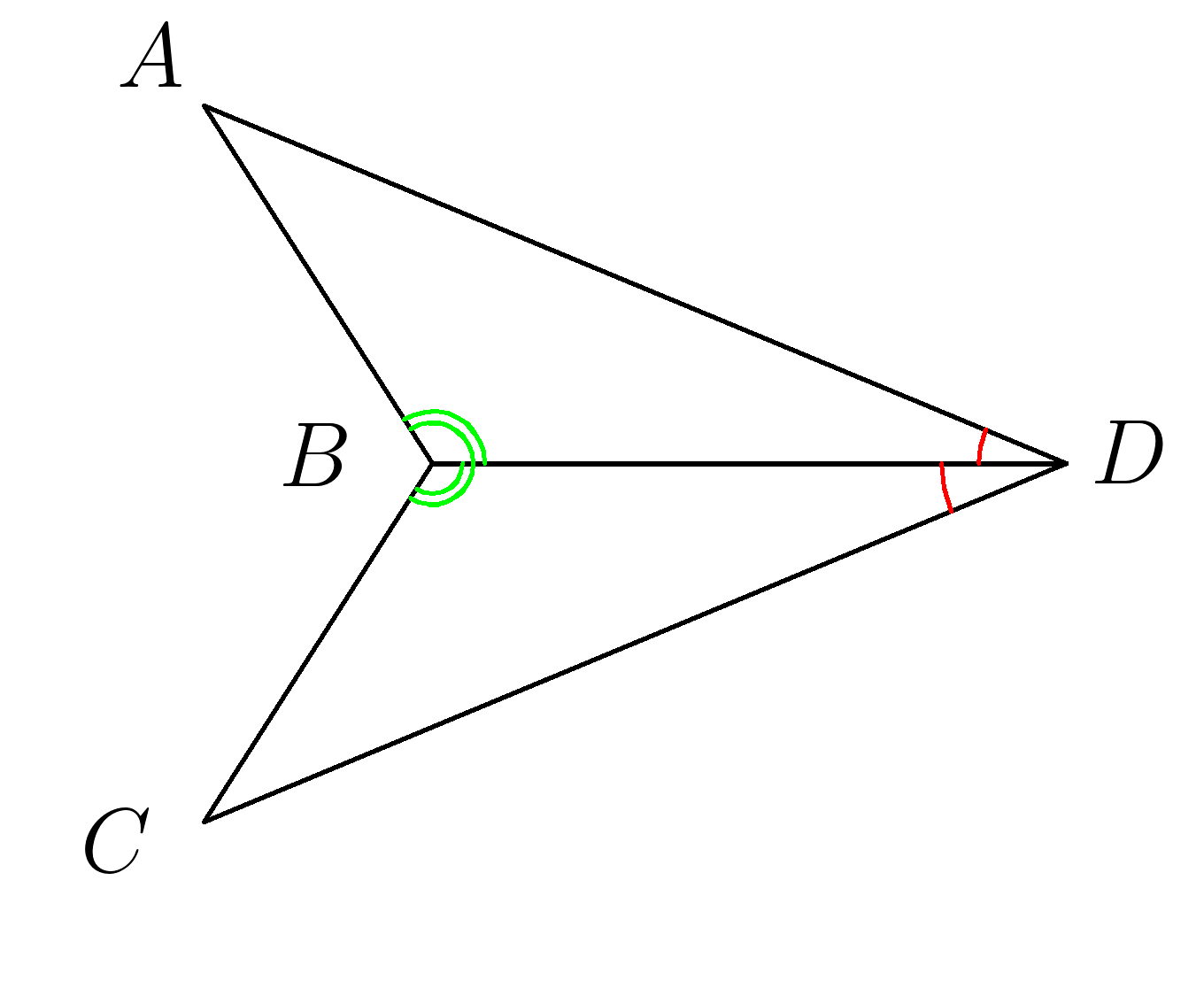
3. \( ∡ADB=∡BDC \:\: ∡ABD=∡CBD \) . Доказать равенство треугольников \(ADB и BDC \).

Показать подсказку Показать решение Видеорешение

\( BD Общая \)

Дано: \(∡ADB=∡BDC , \: ∡ABD=∡CBD \)

Доказать: \( ΔADB = ΔBDC \)

Доказательство:

\( 1)\:\: ∡ADB=∡BDC \) (по условию)
2) \( ∡ABD=∡CBD \) (по условию)
3) \( BD \) (Общая)
\(\Rightarrow ΔADB = ΔBDC \) по второму признаку.

ПОЗЖЕ

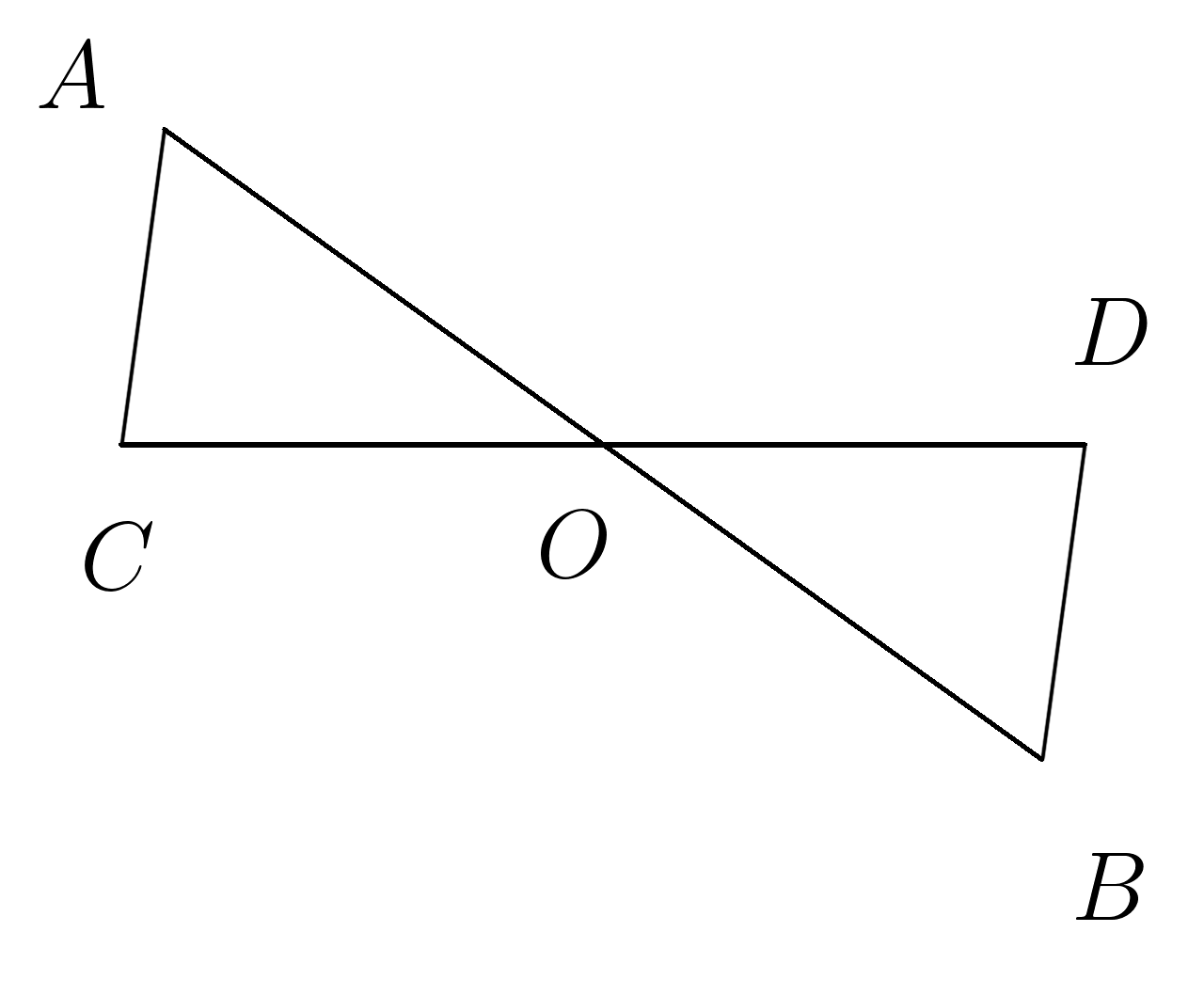
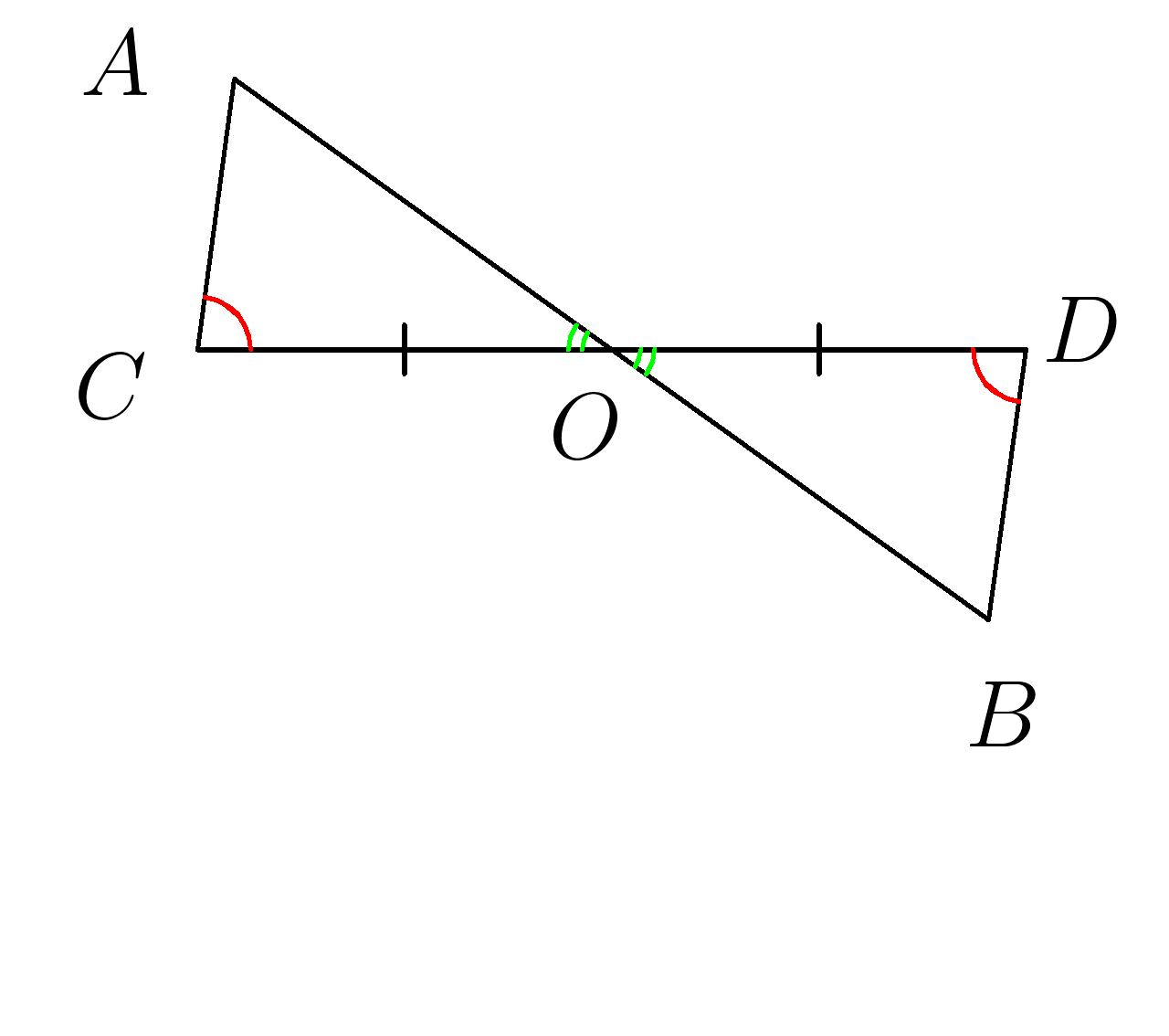
4. Отрезки \(AB и CD \) пересекаются в середине \(O\) отрезка \(CD \;\; , ∡ACO=∡BDO \) . Доказать равенство треугольников \(ACO и BDO \).

Показать подсказку Показать решение Видеорешение

\( ∡AOC=∡BOD \) (Так как они вертикальные)

Дано: \(∡ACO=∡BDO \)
\(O\) середина отрезка \(CD \)

Доказать: \( ΔACO = ΔBDO \)

Доказательство:

\( 1)\:\: ∡ACO=∡BDO \) (по условию)
2) \( CO=OD \) (так как точка \(O \) середина \(CD \) )
3) \( ∡AOC=∡BOD \) (Так как они вертикальные)
\(\Rightarrow ΔAOC = ΔBDO \) по второму признаку.

ПОЗЖЕ

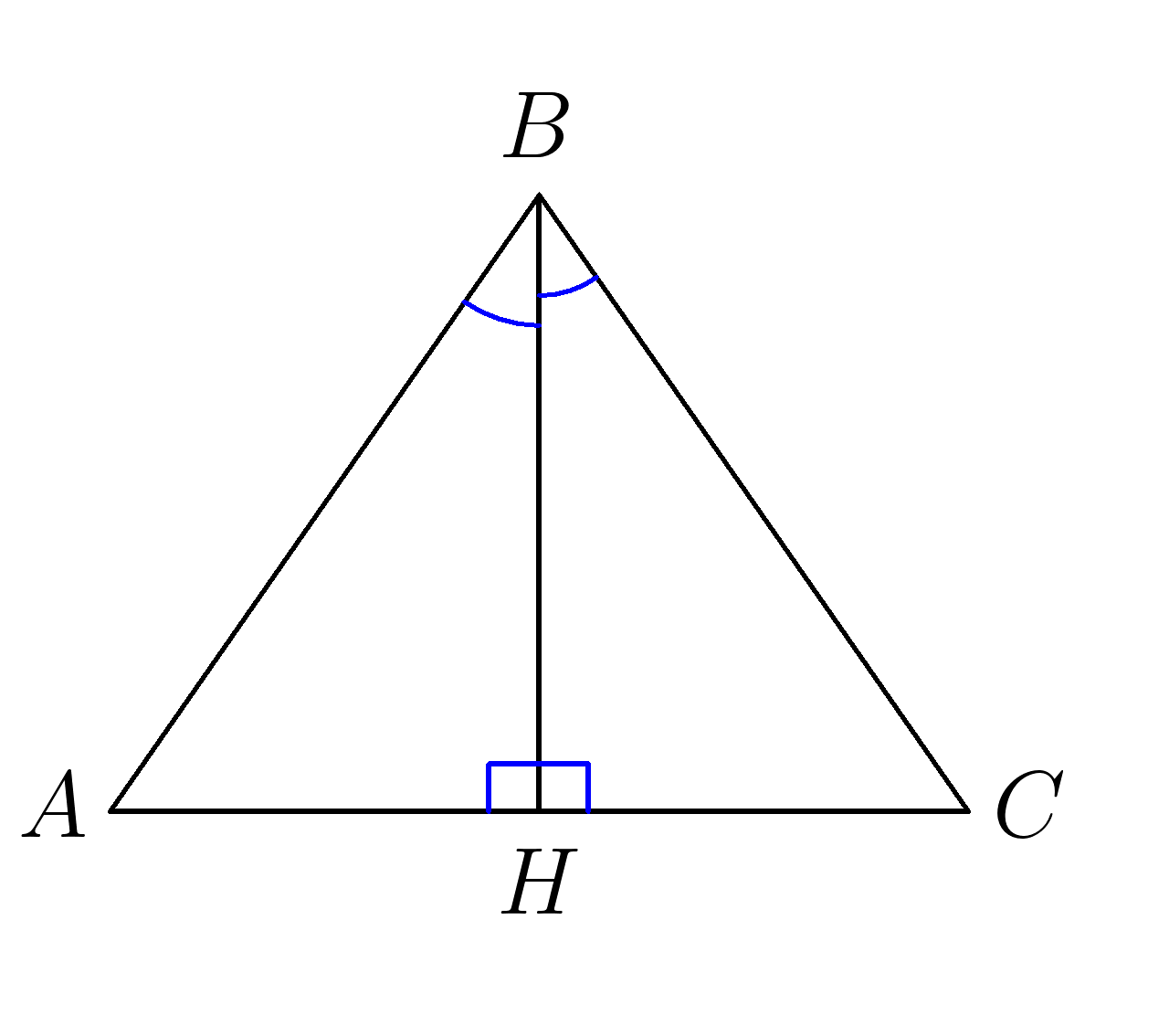
5. Биссекктриса треугольника является его высотой, доказать что этот треугольник равнобедренный.

Показать подсказку Показать решение Видеорешение

Сначала нужно доказать равенство треугольников

Дано: \(BH -\) биссектриса и высота

Доказать: \(ΔABC\) равнобедренный

Доказательство:

\( 1)\:\: ∡AHB=∡BHC=90^0 \) (так как \(BH\) высота )
2) \(∡ABH=∡HBC \) (так как \(BH\) биссектриса )
3) \(BH\) общая
\(\Rightarrow ΔABH=ΔBHC\) по второму признаку.

В треугольнике \(ABH\;\; AB \) лежит против прямого угла \( AHB \),
а в треугольнике \(BHC\) \(BC\) лежит против прямого угла \( BHC \)
В равных треугольниках против равных углов лежат равные стороны, значит:
\(AB=BC, а ΔABC-равнобедренный\)

ПОЗЖЕ