Площадь треугольника. Задачи

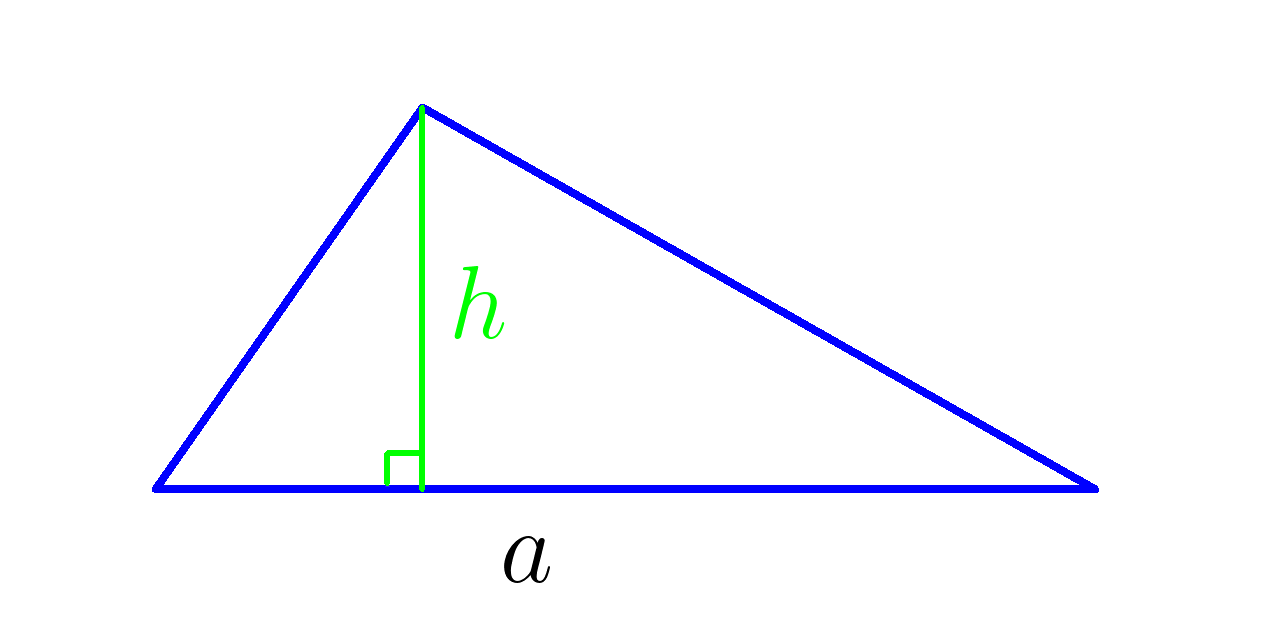
Площадь треугольника равна половине произведения основания на высоту:

\( S=\dfrac{1}{2}ah \)

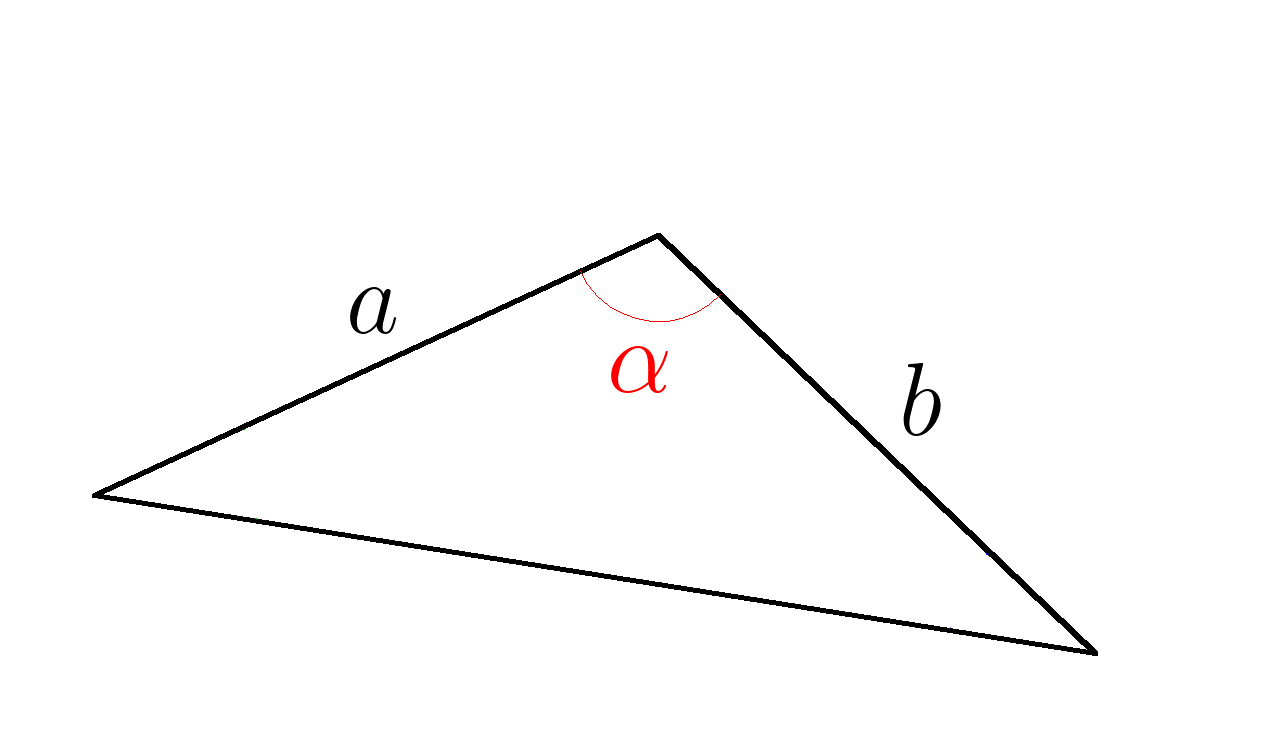
Площадь треугольника равна половине произведения любых двух его сторон на синус угла между ними:

\( S=\dfrac{1}{2}ab \cdot sin \; \alpha \)

1. Высота треугольника на рисунке \( h=4 \) ,а основание \(a=12 \). Найти площадь треугольника
Показать ответ Показать решение Видеорешение

Ответ: \( S=24 \)

\( S=\dfrac{1}{2}ah =\dfrac{1}{2} \cdot 12 \cdot 4=24 \)

Ответ: \( S=24 \)

ПОЗЖЕ

2. Высота треугольника на рисунке \( h=8 \) ,а основание \(a=20 \). Найти площадь треугольника
Показать ответ Показать решение Видеорешение

Ответ: \( S=80 \)

\( S=\dfrac{1}{2}ah =\dfrac{1}{2} \cdot 20 \cdot 8=80 \)

Ответ: \( S=80 \)

ПОЗЖЕ

3. Высота треугольника на рисунке \( h=2 \) ,а основание \(a=5 \). Найти площадь треугольника
Показать ответ Показать решение Видеорешение

Ответ: \( S=5 \)

\( S=\dfrac{1}{2}ah =\dfrac{1}{2} \cdot 5 \cdot 2=5 \)

Ответ: \( S=5 \)

ПОЗЖЕ

4. Площадь треугольника на рисунке \( S=30 \) ,а основание \(a=12 \). Найти высоту \(h\)
Показать ответ Показать решение Видеорешение

Ответ: \( h=5 \)

\( S=\dfrac{1}{2}ah \)

\( S=\dfrac{ah}{2} \)

\(h=\dfrac{2S}{a} \)

\(h=\dfrac{2S}{a}=\dfrac{2\cdot 30}{12}=5 \)

Ответ: \( h=5 \)

ПОЗЖЕ

5. Площадь треугольника на рисунке \( S=70 \) ,а основание \(a=35 \). Найти высоту \(h\)
Показать ответ Показать решение Видеорешение

Ответ: \( h=4 \)

\( S=\dfrac{1}{2}ah \)

\( S=\dfrac{ah}{2} \)

\(h=\dfrac{2S}{a} \)

\(h=\dfrac{2S}{a}=\dfrac{2\cdot 70}{35}=4 \)

Ответ: \( h=4 \)

ПОЗЖЕ

6. Площадь треугольника на рисунке \( S=175 \) ,а высота \(h=25 \). Найти основание \(a\)
Показать ответ Показать решение Видеорешение

Ответ: \( a=14 \)

\( S=\dfrac{1}{2}ah \)

\( S=\dfrac{ah}{2} \)

\(a=\dfrac{2S}{h} \)

\(h=\dfrac{2S}{h}=\dfrac{2\cdot 175}{25}=14 \)

Ответ: \( a=14 \)

ПОЗЖЕ

7. Площадь треугольника на рисунке \( S=225 \) ,а высота \(h=50 \). Найти основание \(a\)
Показать ответ Показать решение Видеорешение

Ответ: \( a=9 \)

\( S=\dfrac{1}{2}ah \)

\( S=\dfrac{ah}{2} \)

\(a=\dfrac{2S}{h} \)

\(h=\dfrac{2S}{h}=\dfrac{2\cdot 225}{50}=9 \)

Ответ: \( a=14 \)

ПОЗЖЕ

8. Площадь треугольника на рисунке \( S=14,5 \) ,а высота \(h=2 \). Найти основание \(a\)
Показать ответ Показать решение Видеорешение

Ответ: \( a=14,5 \)

\( S=\dfrac{1}{2}ah \)

\( S=\dfrac{ah}{2} \)

\(a=\dfrac{2S}{h} \)

\(h=\dfrac{2S}{h}=\dfrac{2\cdot 14,5}{2}=14,5 \)

Ответ: \( a=14 \)

ПОЗЖЕ

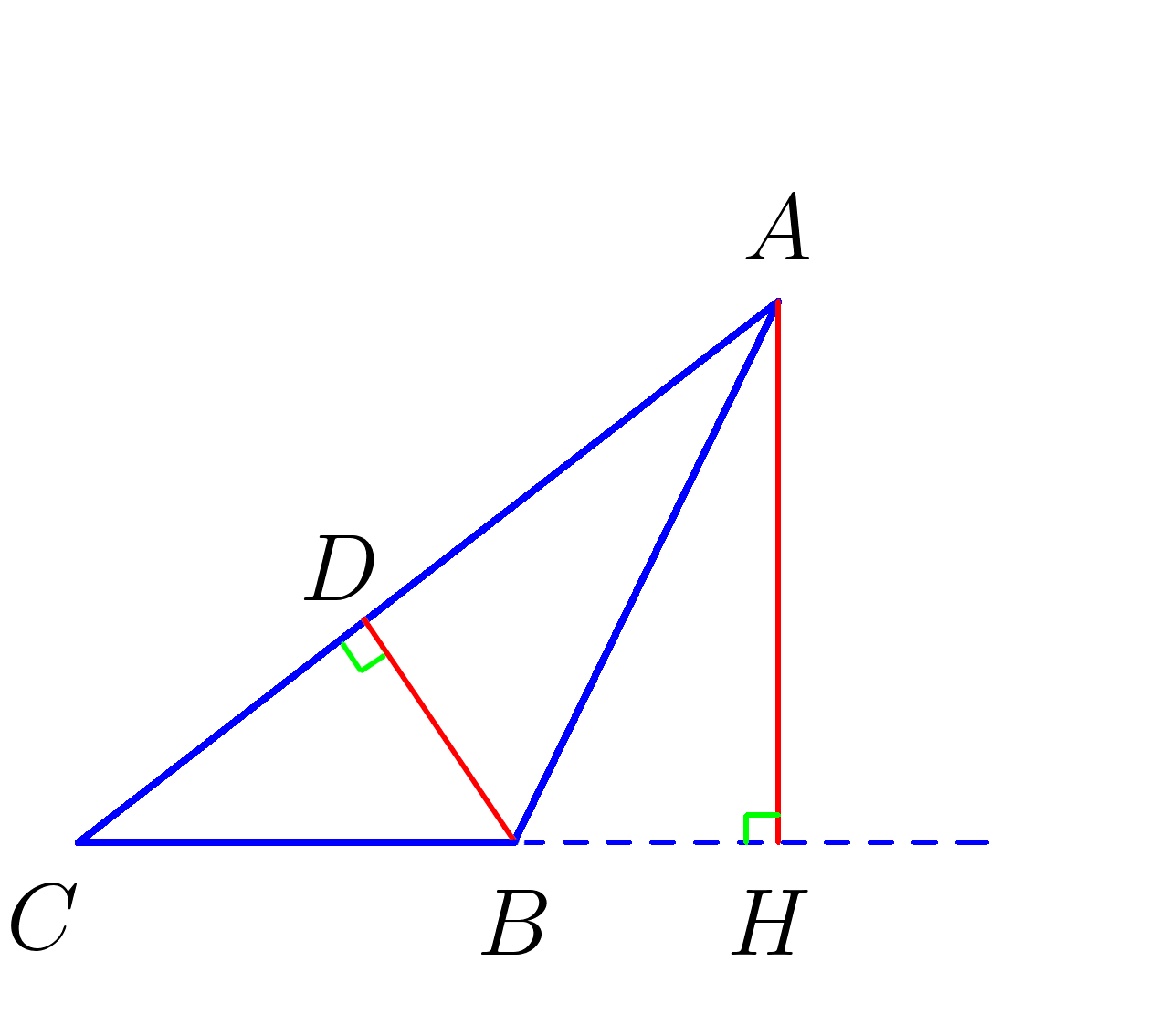
9. \(CB=4, \;\; AH=5, \;\; DB=2. \) Найти \(AC \)
Показать ответ Показать решение Видеорешение

Ответ: \( AC=10 \)

\( S=\dfrac{CB \cdot AH}{2}=\dfrac{4 \cdot 5}{2}= 10 \)

\( S=\dfrac{AC \cdot DB}{2}=10 \)

\( \dfrac{AC \cdot 2}{2}=10 \)

\( AC=10 \)

Ответ: \( AC=10 \)

Более рациональное решение :

\( \dfrac{CB \cdot AH}{2}=\dfrac{AC \cdot DB}{2} \)

\( CB \cdot AH=AC \cdot DB \)

\( AC=\dfrac{CB \cdot AH}{DB}=\dfrac{4 \cdot 5}{2}=10 \)

Ответ: \( AC=10 \)

ПОЗЖЕ

10. \(CB=12, \;\; AH=15, \;\; DB=6. \) Найти \(AC \)
Показать ответ Показать решение Видеорешение

Ответ: \( AC=30 \)

\( S=\dfrac{CB \cdot AH}{2}=\dfrac{12 \cdot 15}{2}= 90 \)

\( S=\dfrac{AC \cdot DB}{2}=90 \)

\( \dfrac{AC \cdot 6}{2}=90 \)

\( AC=30 \)

Ответ: \( AC=30 \)

Более рациональное решение :

\( \dfrac{CB \cdot AH}{2}=\dfrac{AC \cdot DB}{2} \)

\( CB \cdot AH=AC \cdot DB \)

\( AC=\dfrac{CB \cdot AH}{DB}=\dfrac{12 \cdot 15}{6}=30 \)

Ответ: \( AC=30 \)

ПОЗЖЕ

11. \(AC=17, \;\; DB=8, \;\; AH=10. \) Найти \(CB \)
Показать ответ Показать решение Видеорешение

Ответ: \( CB=13,6 \)

\( S=\dfrac{AC \cdot DB}{2}= \dfrac{17 \cdot 8}{2}=68 \)

\( S=\dfrac{CB \cdot AH}{2}= 68 \)

\( \dfrac{CB \cdot 10}{2}= 68 \)

\( CB=13,6 \)

Ответ: \( CB=13,6 \)

Более рациональное решение :

\( \dfrac{CB \cdot AH}{2}=\dfrac{AC \cdot DB}{2} \)

\( CB \cdot AH=AC \cdot DB \)

\(CB=\dfrac{AC \cdot DB }{AH}=\dfrac{17 \cdot 8 }{10}=13,6 \)

Ответ: \( CB=13,6 \)

ПОЗЖЕ

12. Угол \( \alpha \) между сторонами треугольника \( a \ и \ b \) составляет \( 30^0 . \) Найдите площадь этого треугольника, если \(a=10, \ \ b=11 . \)
Показать ответ Показать решение Видеорешение

Ответ: \( S=27,5 \)

Запишем формулу нахождения площади треугольника:

\( S=\dfrac{1}{2}ab \cdot sin \; \alpha \)

\( S=\dfrac{1}{2} \cdot 10 \cdot 11 \cdot sin \; 30^{\circ}=5 \cdot 11 \cdot 0,5=27,5 \)

Ответ: \( S=27,5 \)

ПОЗЖЕ

13. В треугольнике, изображенном на рисунке угол \( \alpha=45^{\circ} , \ \) а стороны \( a=\sqrt{8}, \ \ b=51 . \)
Найдите площадь этого треугольника.
Показать ответ Показать решение Видеорешение

Ответ: \( S=51 \)

Запишем формулу нахождения площади треугольника:

\( S=\dfrac{1}{2}ab \cdot sin \; \alpha \)

\( S=\dfrac{1}{2} \cdot \sqrt{8} \cdot 51 \cdot sin \; 45^{\circ}= \dfrac{1}{2} \cdot \sqrt{8} \cdot 51 \cdot \dfrac{\sqrt{2}}{2} = 51 \)

Ответ: \( S=51 \)

ПОЗЖЕ