Описанная окружность

Около любого треугольника можно описать окружность

Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.
     
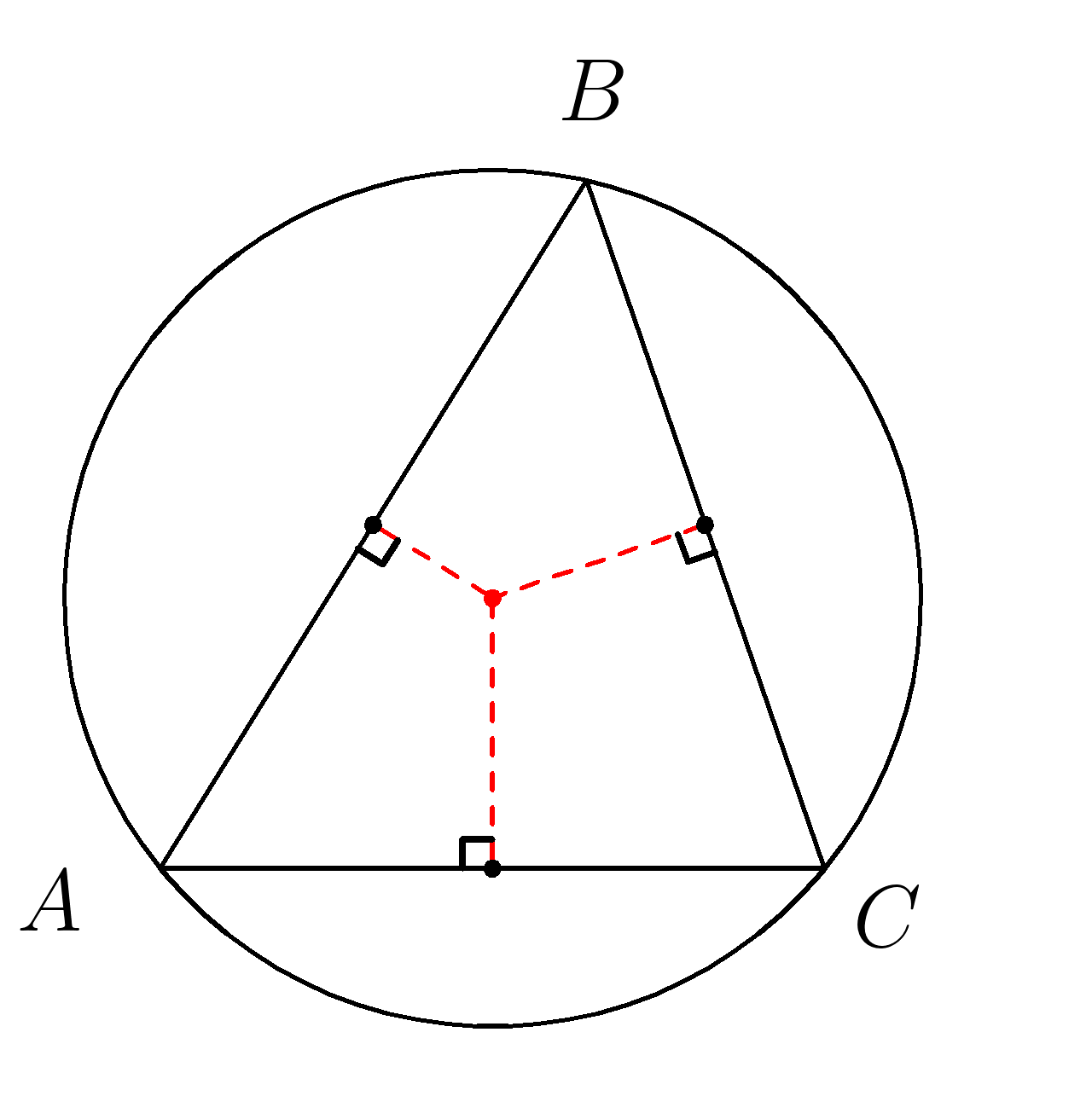
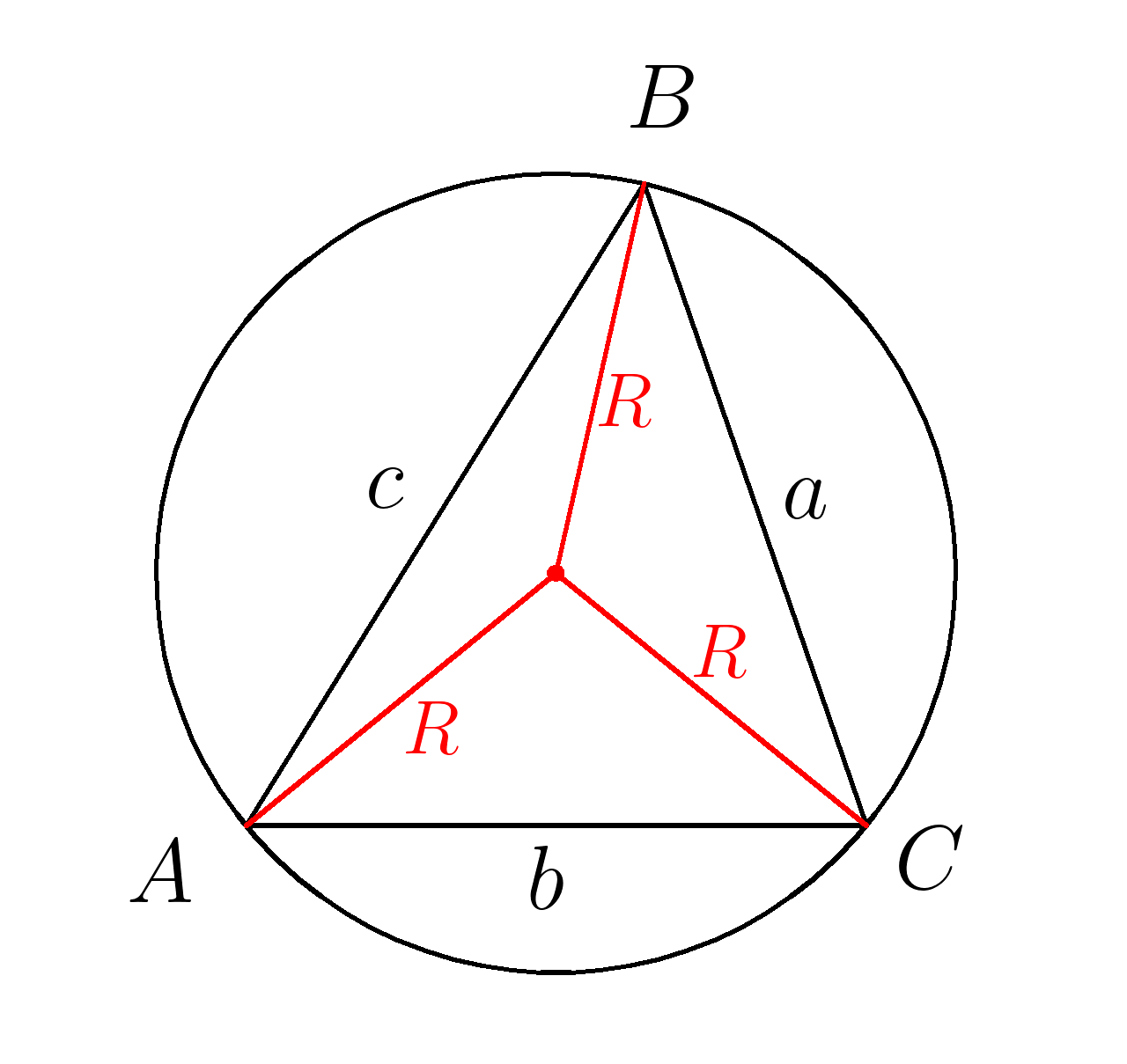
\(R= \dfrac{abc}{4S} \)

\(R\) -радиус описанной окружности
\(S\) -площадь треугольника
\(a\) - сторона \(BC\)
\(b\) - сторона \(AC\)
\(c\) - сторона \(AB\)

---

  

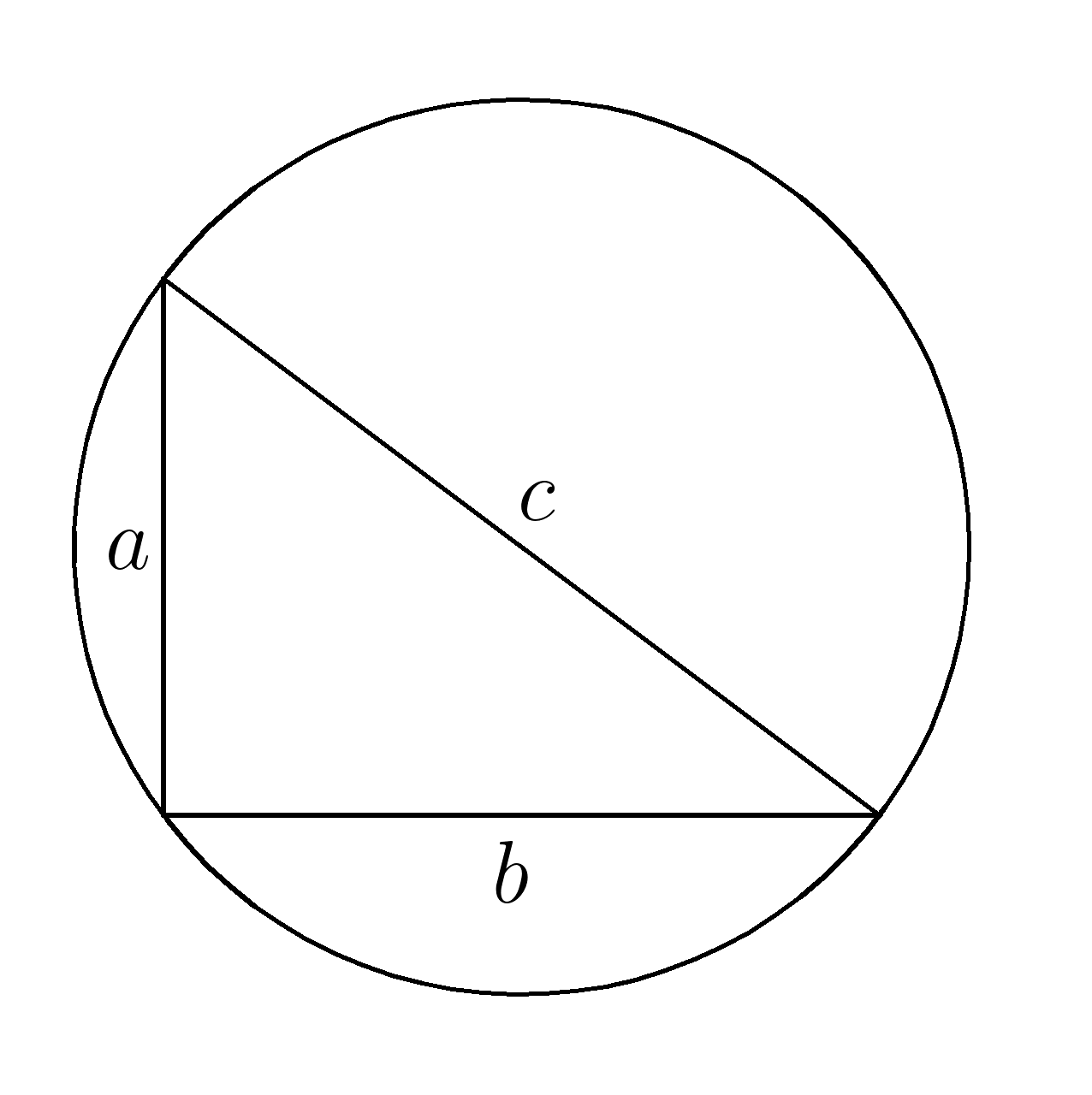
1.  Найти радиус описанной окружности, если площадь треугольника \(S=6 \; \), а стороны \(\; a=3, \; b=4, \; c=5 \)
Показать ответ Показать решение Видеорешение

ПОЗЖЕ

---

  

2.  Найти радиус описанной окружности, если площадь треугольника \(S=30 \; \), а стороны \(\; a=5, \; b=12, \; c=13 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(R=6,5\)

\(R= \dfrac{abc}{4S}= \dfrac{5 \cdot 12 \cdot 13 }{4 \cdot 30}= 6,5 \)

Ответ: \(R=6,5\)

ПОЗЖЕ

---

  

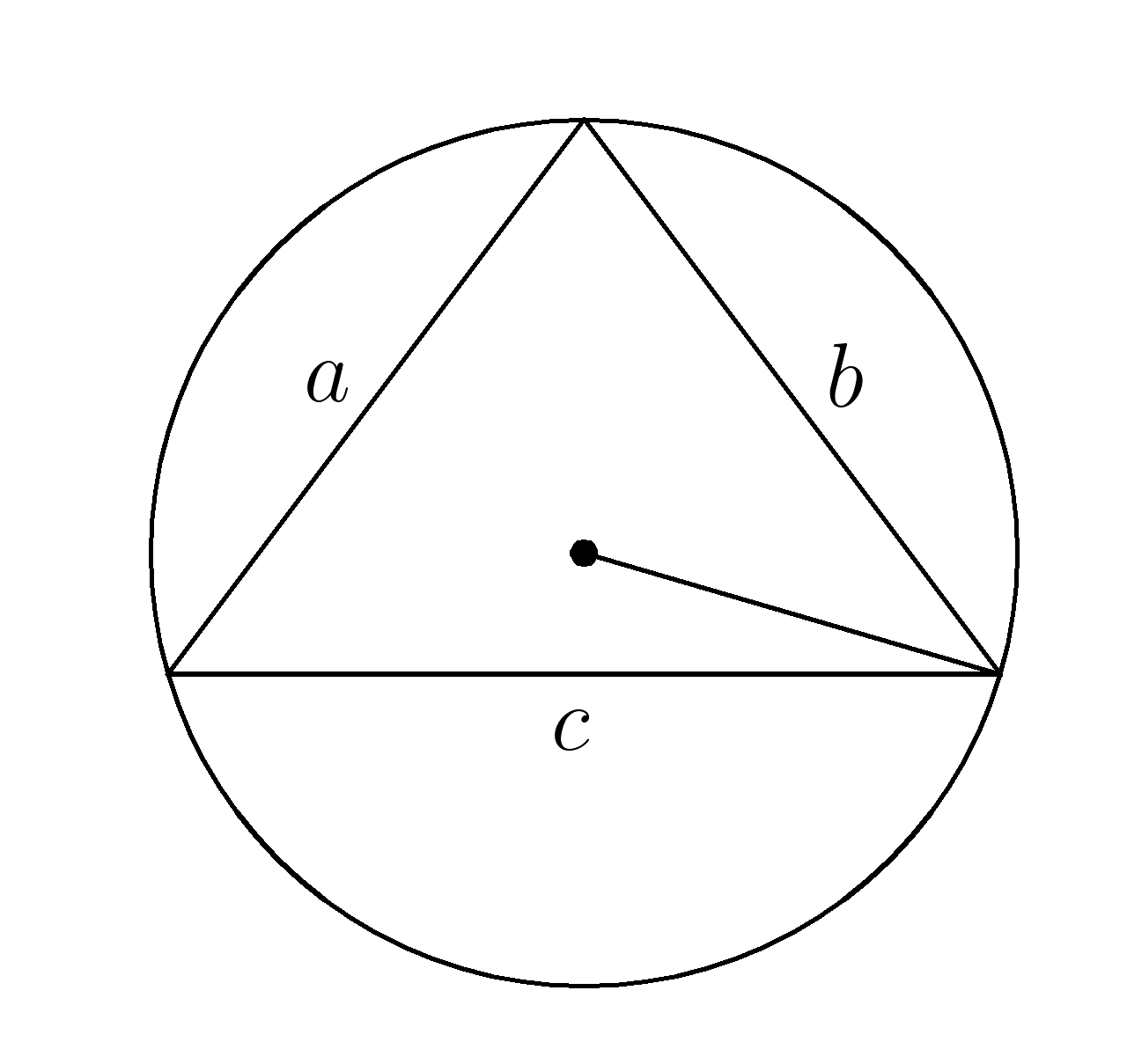
3.  Найти радиус описанной окружности, если площадь треугольника \(S=12 \; \), а стороны \(\; a=5, \; b=5, \; c=6 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(R=3,125\)

\(R= \dfrac{abc}{4S}= \dfrac{5 \cdot 5 \cdot 6 }{4 \cdot 12}= 3,125 \)

Ответ: \(R=3,125\)

ПОЗЖЕ

---

  

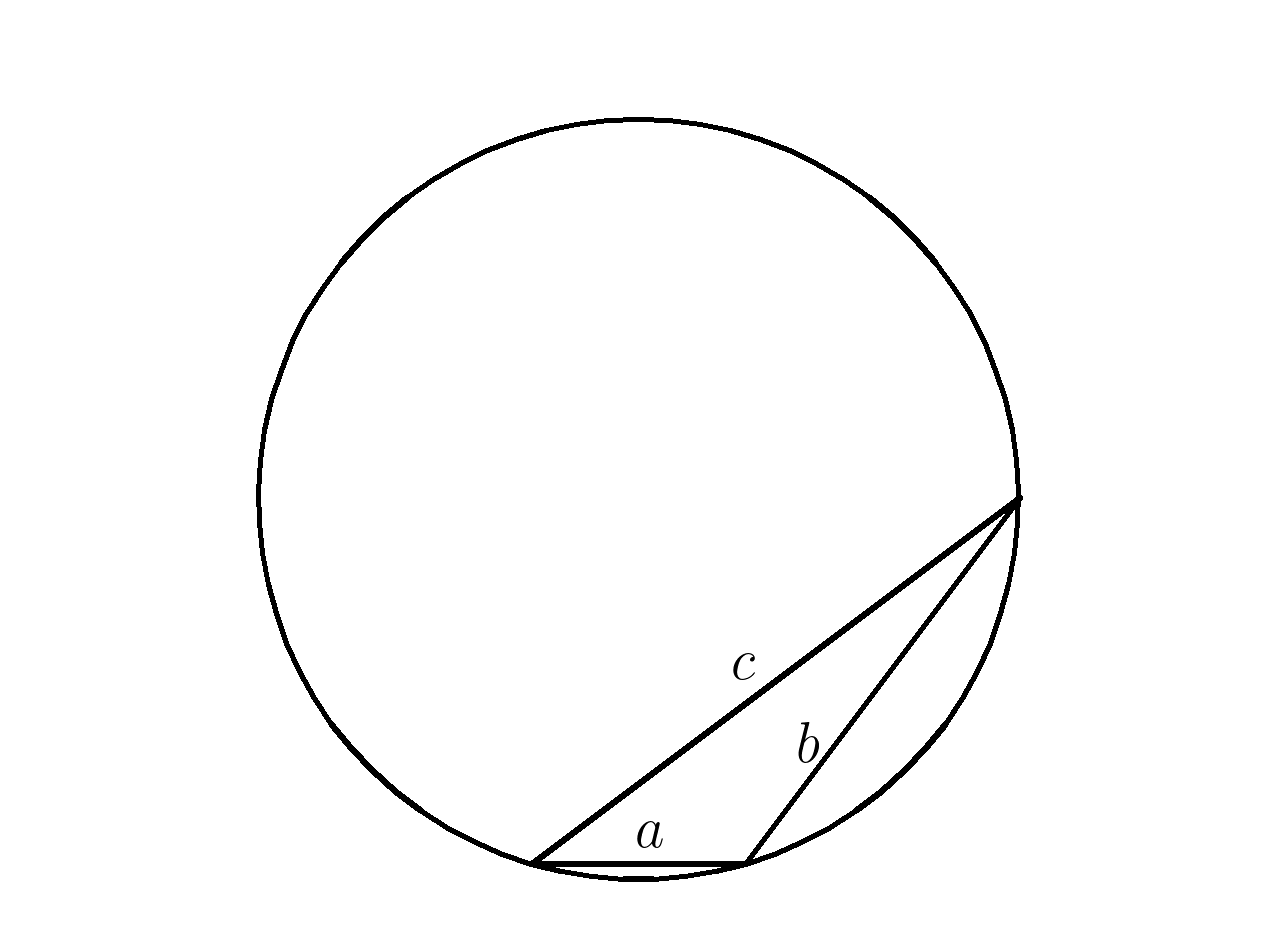
4.  Найти радиус описанной окружности, если площадь треугольника \(S=168 \; \), а стороны \(\; a=14, \; b=30, \; c=40 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(R=25\)

\(R= \dfrac{abc}{4S}= \dfrac{14 \cdot 30 \cdot 40 }{4 \cdot 168}= 25 \)

Ответ: \(R=25\)

ПОЗЖЕ

---

  

5.  Найти сторону \(a\) треугольника, если радиус описанной окружности \(R=12,5\), площадь треугольника \(S=42 \; \), а стороны \( \; b=15, \; c=20 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(a=7 \)

\(R= \dfrac{abc}{4S} \)

\(12,5= \dfrac{a \cdot 15 \cdot 20}{4 \cdot 42 } \)

\(12,5= \dfrac{a \cdot 300}{168 } \)

\(a=\dfrac{12,5 \cdot 168}{300} \)

\(a=7 \)
Ответ: \(a=7 \)

Другое, более рациональное решение:

\(a=\dfrac{4SR}{bc}=\dfrac{4\cdot42 \cdot 12,5}{15 \cdot 20}=7 \)

Ответ: \(a=7 \)

ПОЗЖЕ

---

  

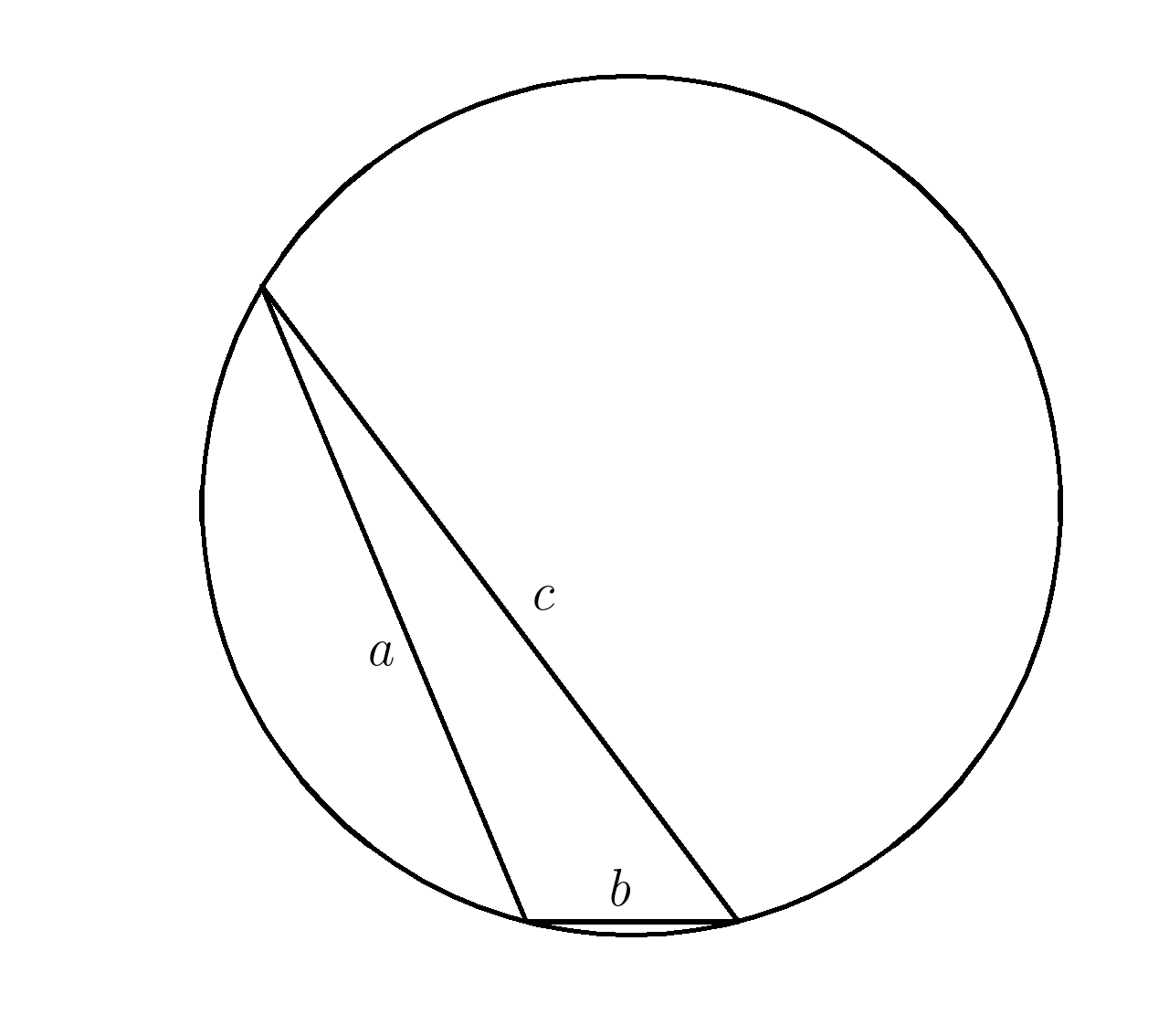
6.  Найти сторону \(b\) треугольника, если радиус описанной окружности \(R=16,25\), площадь треугольника \(S=96 \; \), а стороны \( \; a=26, \; c=30 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(b=8 \)

\(R= \dfrac{abc}{4S} \)

\(16,25= \dfrac{b \cdot 26\cdot 30}{4 \cdot 96 } \)

\(16,25= \dfrac{b \cdot 780 }{384 } \)

\(b=\dfrac{16,25 \cdot 384}{780} \)

\(b=8 \)
Ответ: \(b=8 \)

Другое, более рациональное решение:

\(b=\dfrac{4SR}{ac}=\dfrac{4\cdot96 \cdot 16,25}{26 \cdot 30}=8 \)

Ответ: \(b=8 \)

ПОЗЖЕ

---