Вписанная окружность

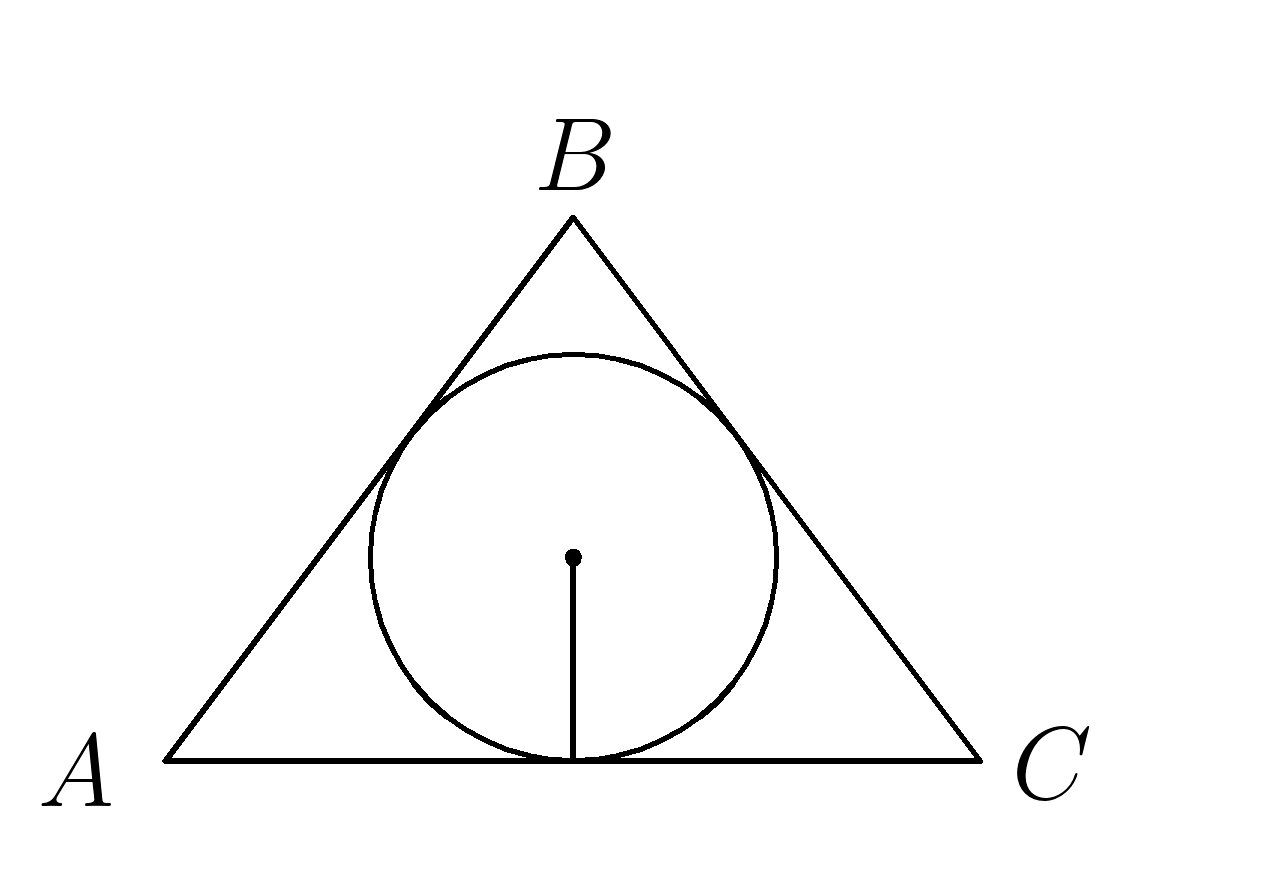
В любой треугольник можно вписать окружность
Центром окружности является точка пересечения биссектрис треугольника
     


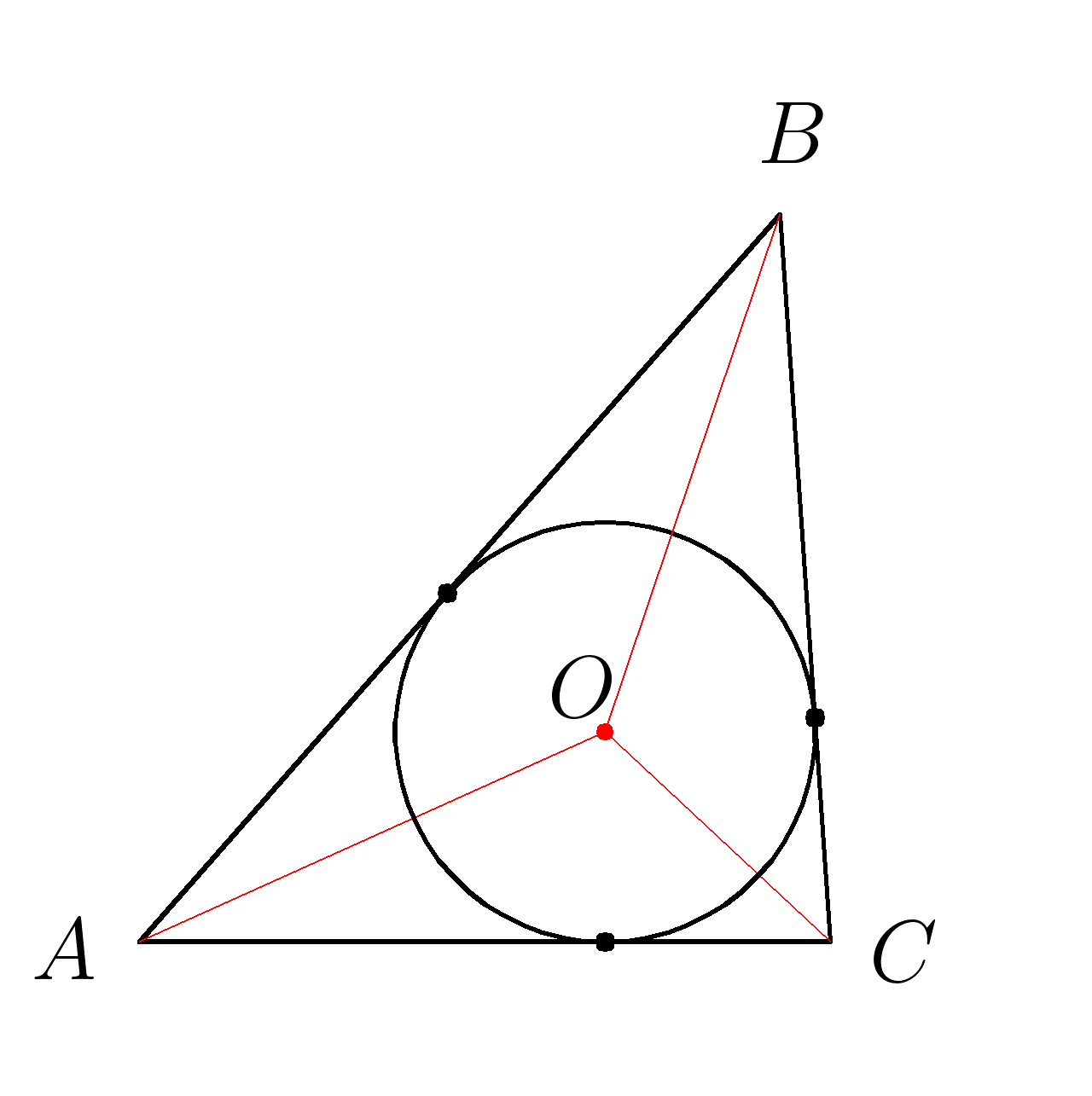
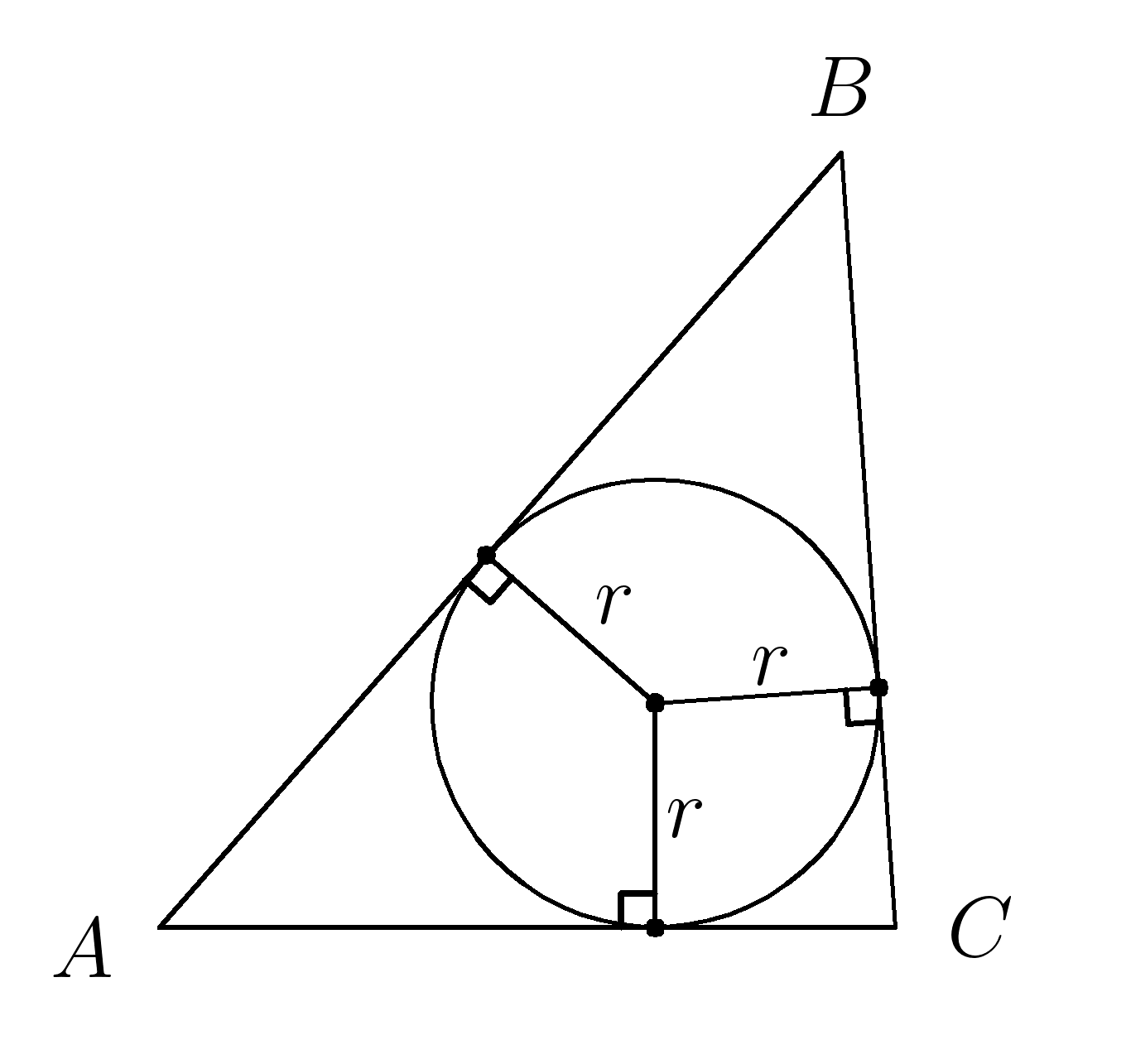
\( S=\dfrac{P}{2}\cdot r \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P=AB+AC+BC \)

\(S\)- площадь треугольника
\(P\)- периметр(сумма сторон) треугольника
\(r\)- радиус вписанной окружности

---

  

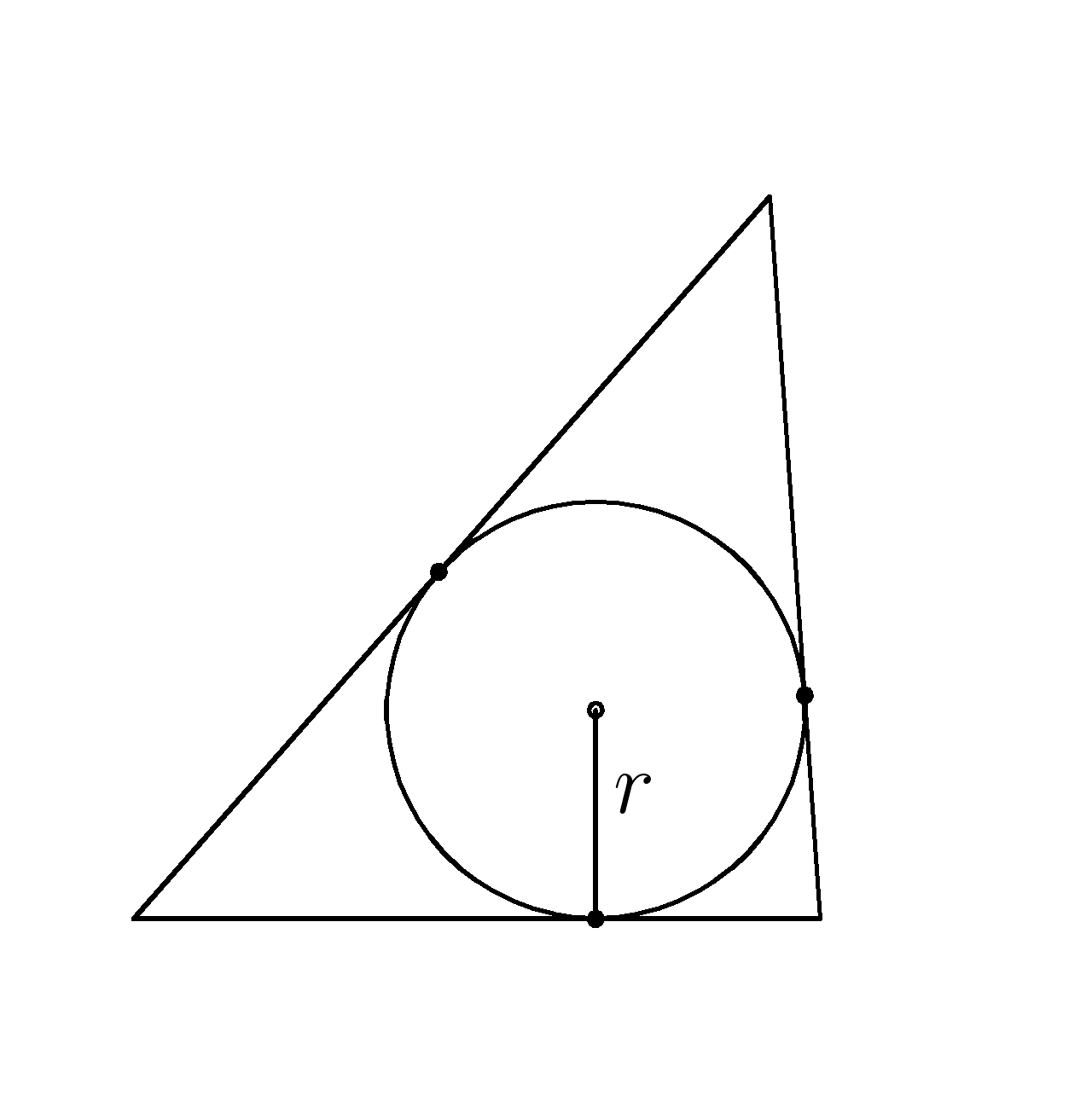
1.  Найти площадь \(S \) треугольника ,в который вписана окружность радиусом \(r=3\) , если ее периметр \(P\) равен \(30 \)
Показать ответ Показать решение Видеорешение

ПОЗЖЕ

---

  

2.  Найти площадь \(S \) треугольника ,в который вписана окружность радиусом \(r=5\) , если ее периметр \(P\) равен \(40 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(S=100\)

\( S=\dfrac{P}{2}\cdot r= \dfrac{40}{2}\cdot 5=100 \)

Ответ: \(S=100\)

ПОЗЖЕ

---

  

3.  Найти площадь \(S \) треугольника ,в который вписана окружность радиусом \(r=8\) , если ее периметр \(P\) равен \(74 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(S=296\)

\( S=\dfrac{P}{2}\cdot r= \dfrac{74}{2}\cdot 8=296 \)

Ответ: \(S=296\)

ПОЗЖЕ

---

  

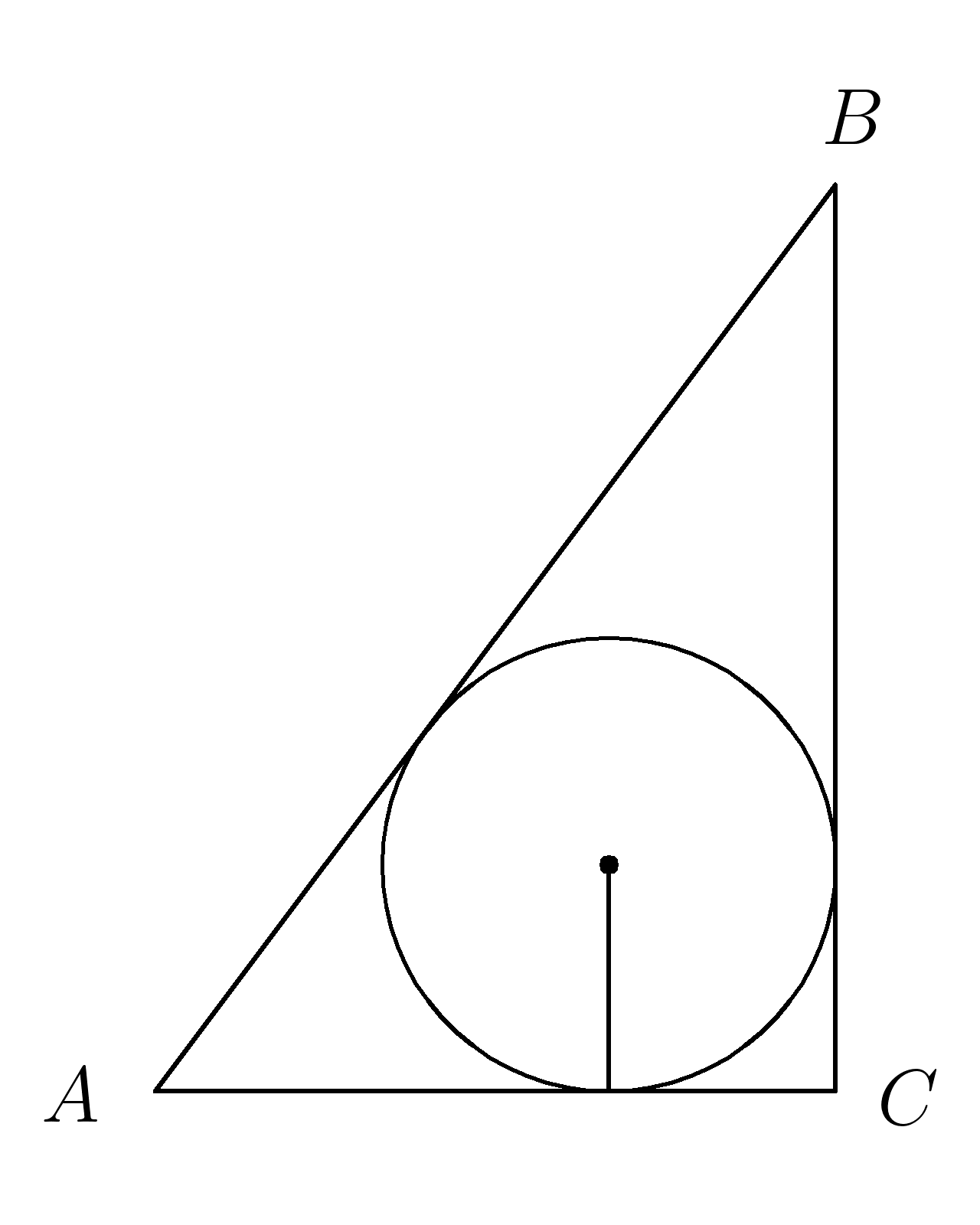
4.  Найти площадь \(S \) треугольника ,в который вписана окружность радиусом \(r=1\) , если \(AB=5, \; AC=4, \; BC=3 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(S=6\)

\(P=AB+AC+BC=5+4+3=12 \)

\( S=\dfrac{P}{2}\cdot r= \dfrac{12}{2}\cdot 1=6 \)

Ответ: \(S=6\)

ПОЗЖЕ

---

  

5.  Найти площадь \(S \) треугольника ,в который вписана окружность радиусом \(r=1,5\) , если \(AB=5, \; AC=6, \; BC=5 \)
Показать ответ Показать решение Видеорешение

  

Ответ: \(S=12\)

\(P=AB+AC+BC=5+6+5=16 \)

\( S=\dfrac{P}{2}\cdot r= \dfrac{16}{2}\cdot 1,5=12 \)

Ответ: \(S=12\)

ПОЗЖЕ

---

  

6.  \(AB=15, \; BC=15, \; AC=18.\; \) Площадь треугольника \(S=108\). Найти радиус вписанной окружности
Показать ответ Показать решение Видеорешение

  

Ответ: \(r=4,5\)

\( S=\dfrac{P}{2}\cdot r\)

\( S=\dfrac{Pr}{2}\)

\( r=\dfrac{2S}{P}\)

\( r=\dfrac{2S}{AB+BC+AC}=\dfrac{2\cdot 108}{15+15+18}=4,5\)

Ответ: \(r=4,5\)

ПОЗЖЕ

---