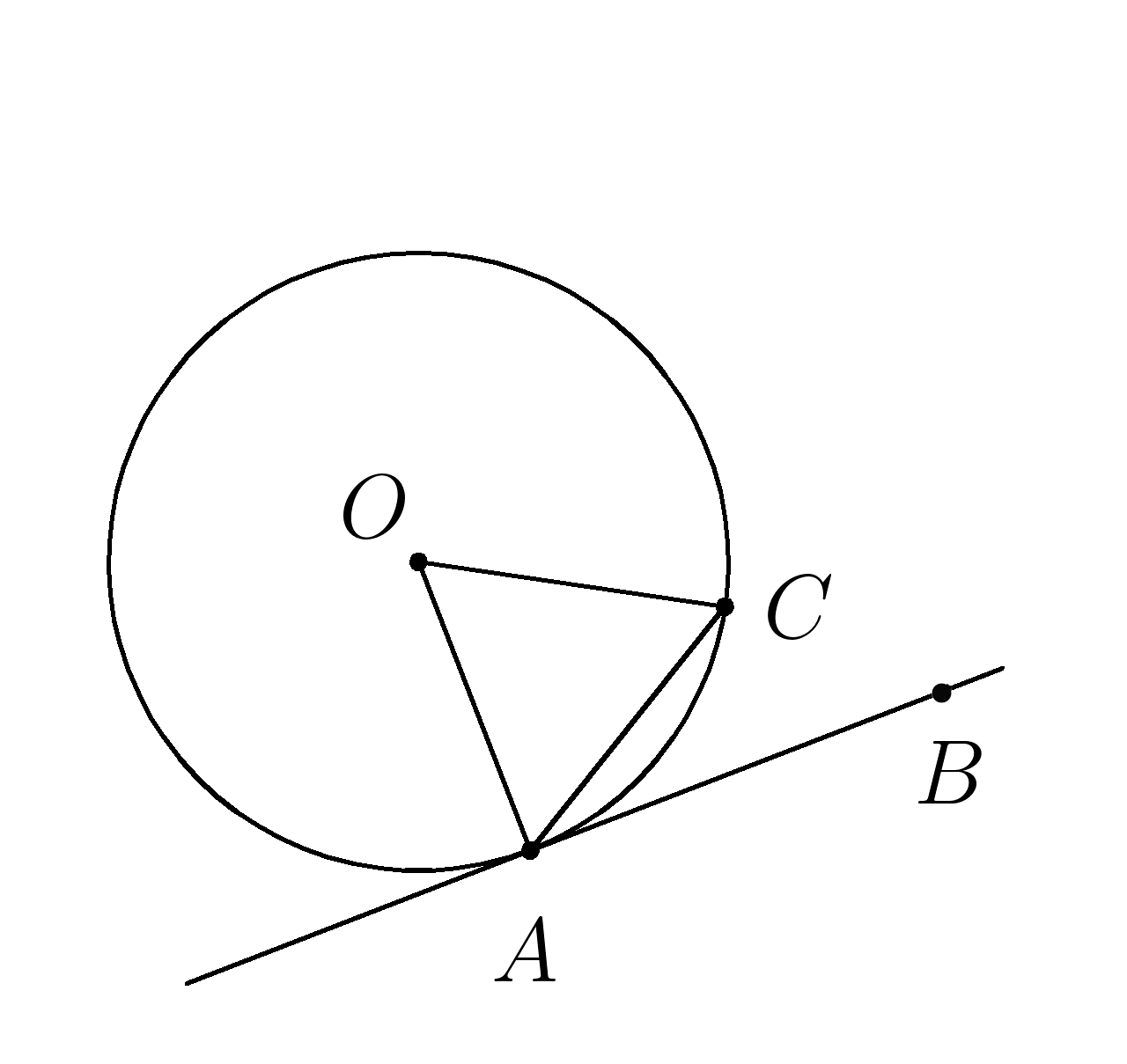
Касательная к окружности .
Касательная к окружности перпендикулярна радиусу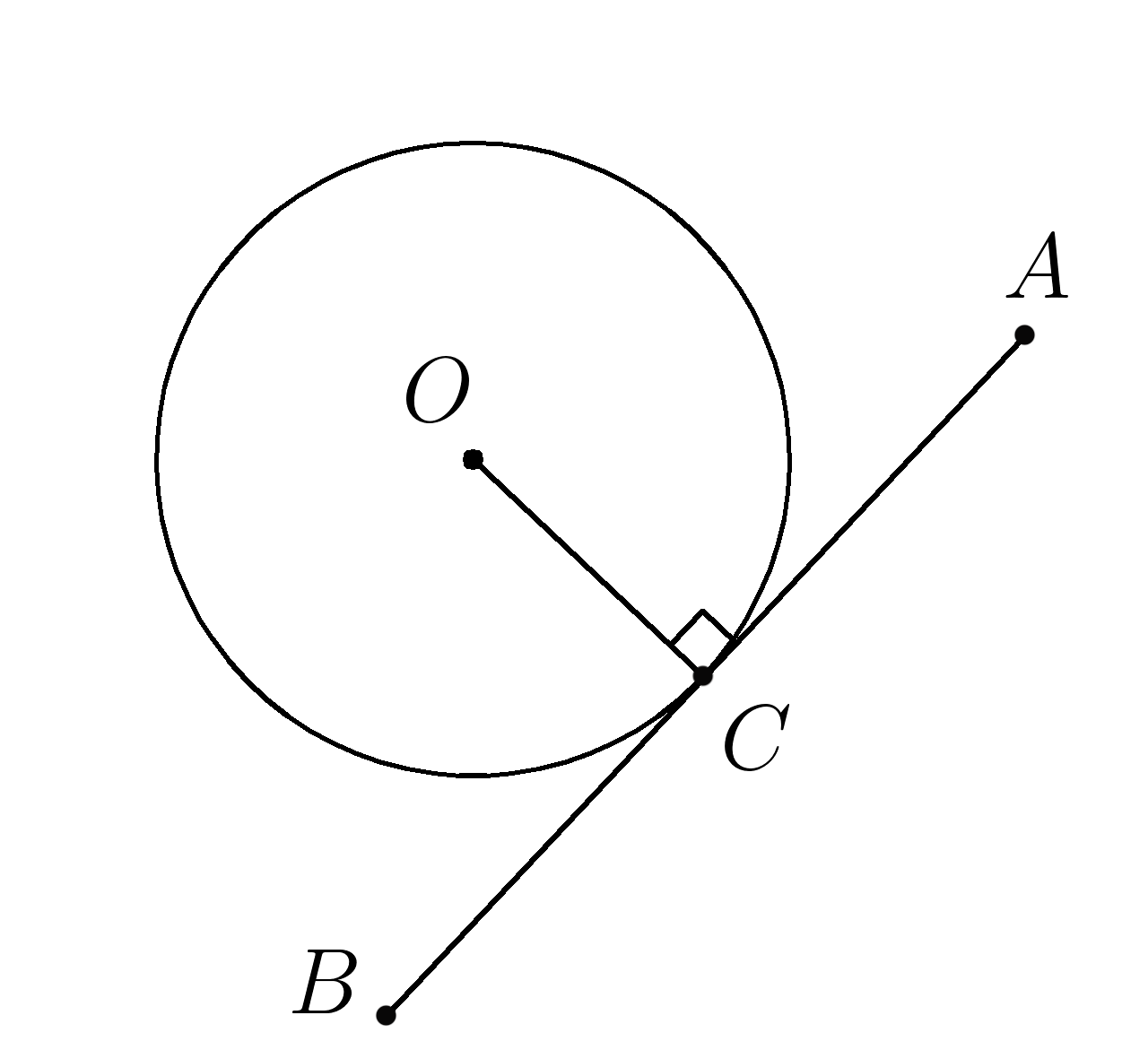
\(AB \perp OC \)
1. Прямая \( AB \) касается окружности в точке \(C, \; OC=3,\; AC=4. \)
Найти \(OA \)
Показать ответ
Показать решение
Видеорешение

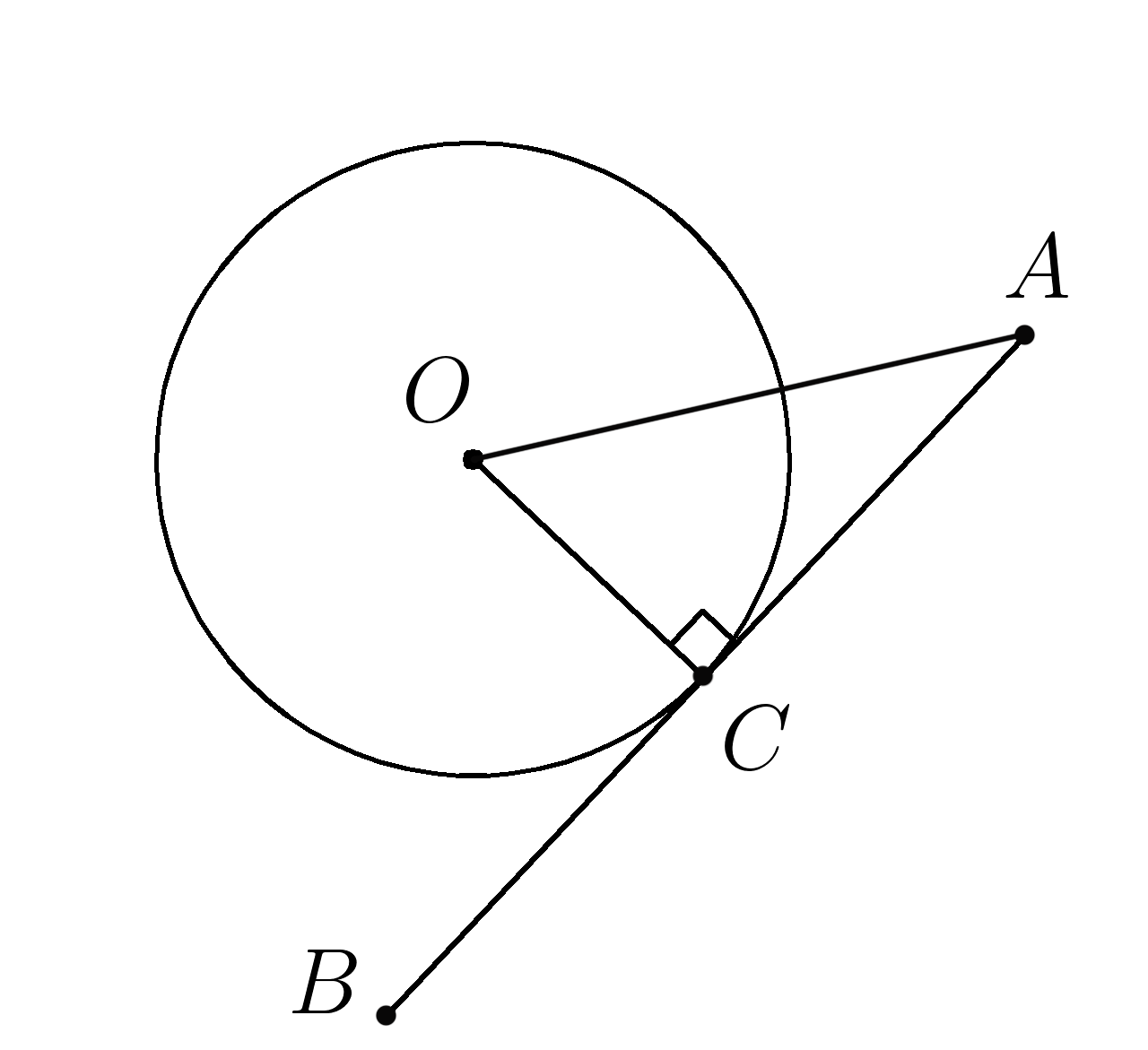
2. Прямая \( AB \) касается окружности в точке \(C, \; OC=5,\; AC=12. \)
Найти \(OA \)
Показать ответ
Показать решение
Видеорешение

3. Прямая \( AB \) касается окружности в точке \(C, \; OA=1,7,\; OC=\dfrac{4}{5}. \)
Найти \(AC \)
Показать ответ
Показать решение
Видеорешение
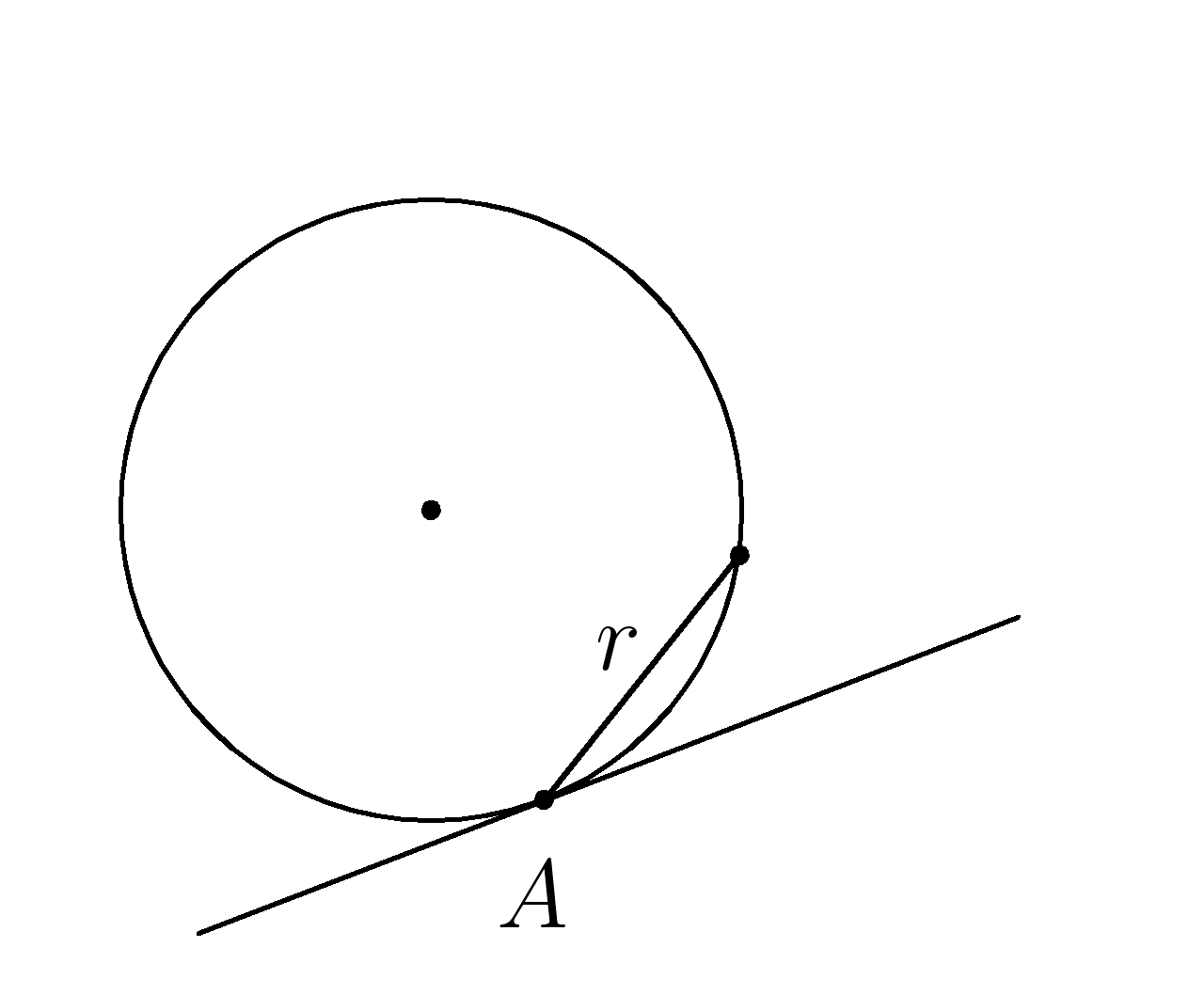
4. Через точку \(A \) окружности проведены касательная и хорда, равная радиусу окружности.
Найти угол между ними.
Показать ответ
Показать решение
Видеорешение
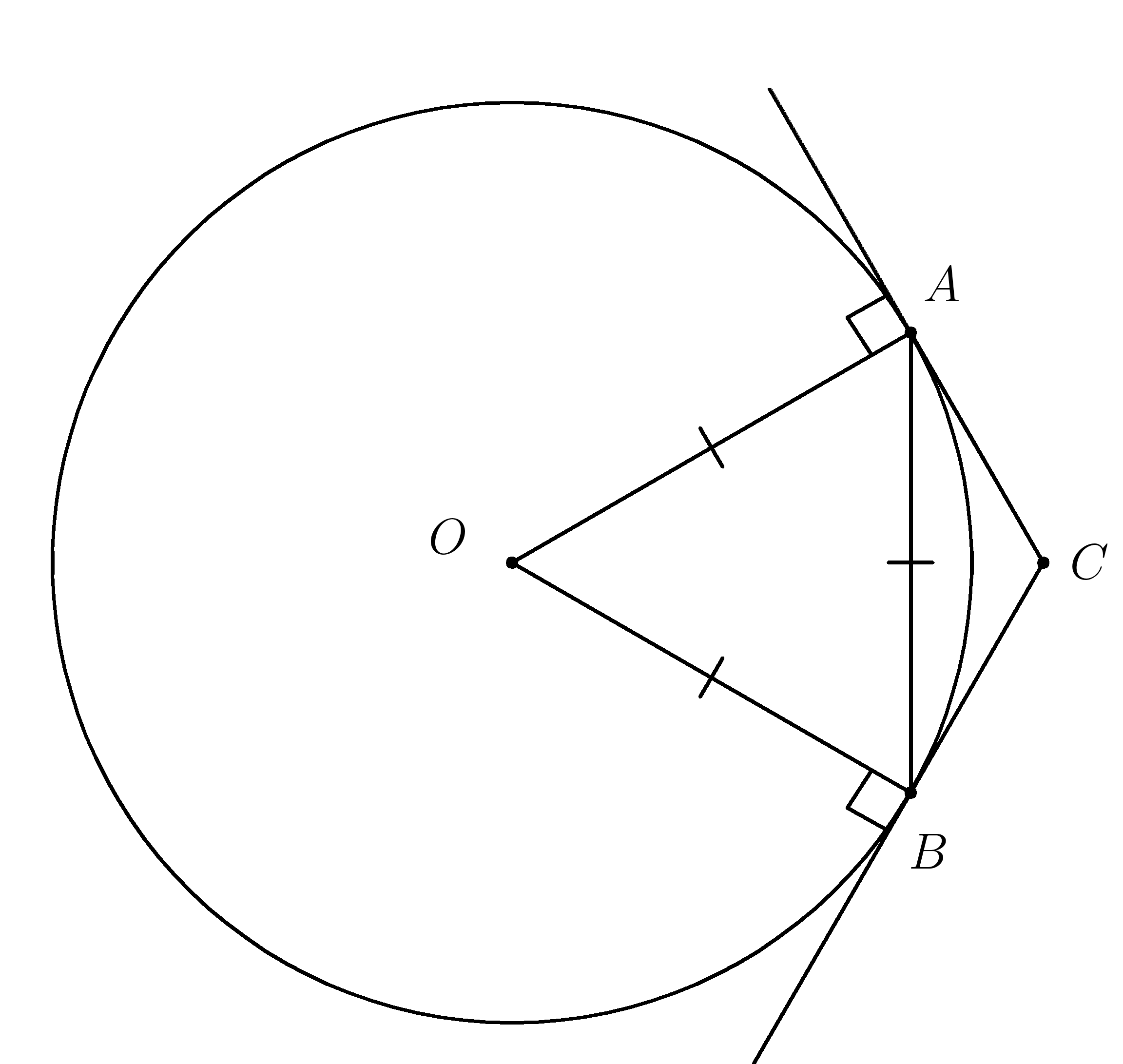
5. Через концы хорды \(AB\), равной радиусу окружности, проведены две касательнае, пересекающиеся в точке \(C \). Найти угол \(ACB\)
Показать ответ
Показать решение
Видеорешение