Подобные треугольники
Простыми словами:
Два треугольника называются подобными если один из них является уменьшенной копией второго
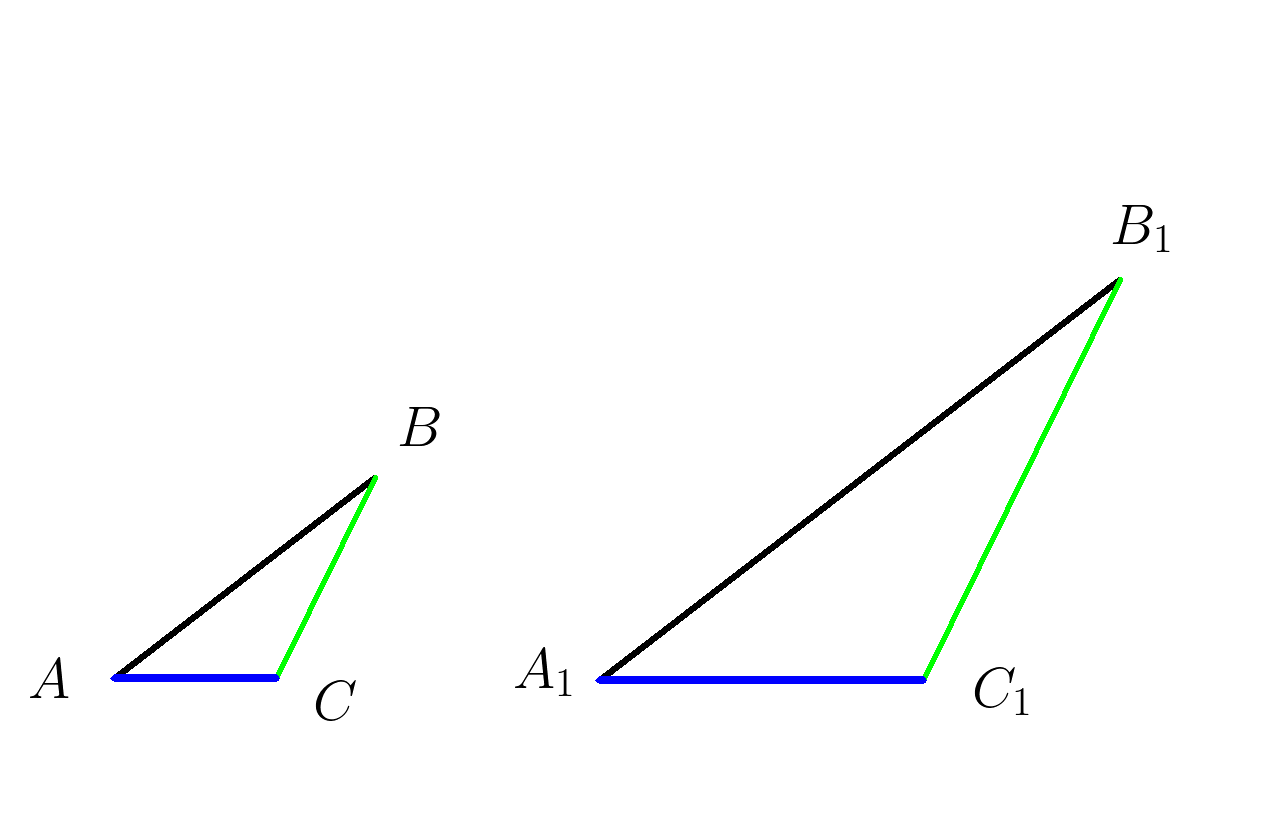
Стороны одного цвета называются сходственными
Знак \( ∾ \) означает подобие
\( \Delta ABC ∾ \Delta A_1B_1C_1 \)
\( \dfrac{A_1B_1}{AB}=\dfrac{A_1C_1}{AC}=\dfrac{B_1C_1}{BC}=k \)
\(k\) это коэффициент подобия
Первый признак подобия:
Если любые два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны
В подобных треугольниках каждый угол одного треугольника соответственно равен одному из углов другого треугольника
В подобных треугольниках против равных углов лежат сходственные стороны
Репетитор по геометрии
8 916 478 10 32

1. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=2, \; A_1B_1=4 , \; BC=1,5 . \) Найти \(B_1C_1 \)
Показать ответ
Показать решение
Видеорешение
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( \angle A=\angle A_1, \; \) значит \( BC и B_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{4}{2}=\dfrac{B_1C_1}{1,5} \)
\( B_1C_1 =3 \)
Ответ: \( B_1C_1 =3 \)

2. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=2, \; A_1B_1=4 , \; AC=1 . \) Найти \(A_1C_1 \)
Показать ответ
Показать решение
Видеорешение
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( AC \) лежит против \(\angle B \),
\( A_1C_1 \) лежит против \(\angle B_1 \)
\( \angle B=\angle B_1, \; \) значит \( AC и A_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{A_1C_1}{AC} \)
\( \dfrac{4}{2}=\dfrac{A_1C_1}{1} \)
\( A_1C_1 =2 \)
Ответ: \( A_1C_1 =2 \)
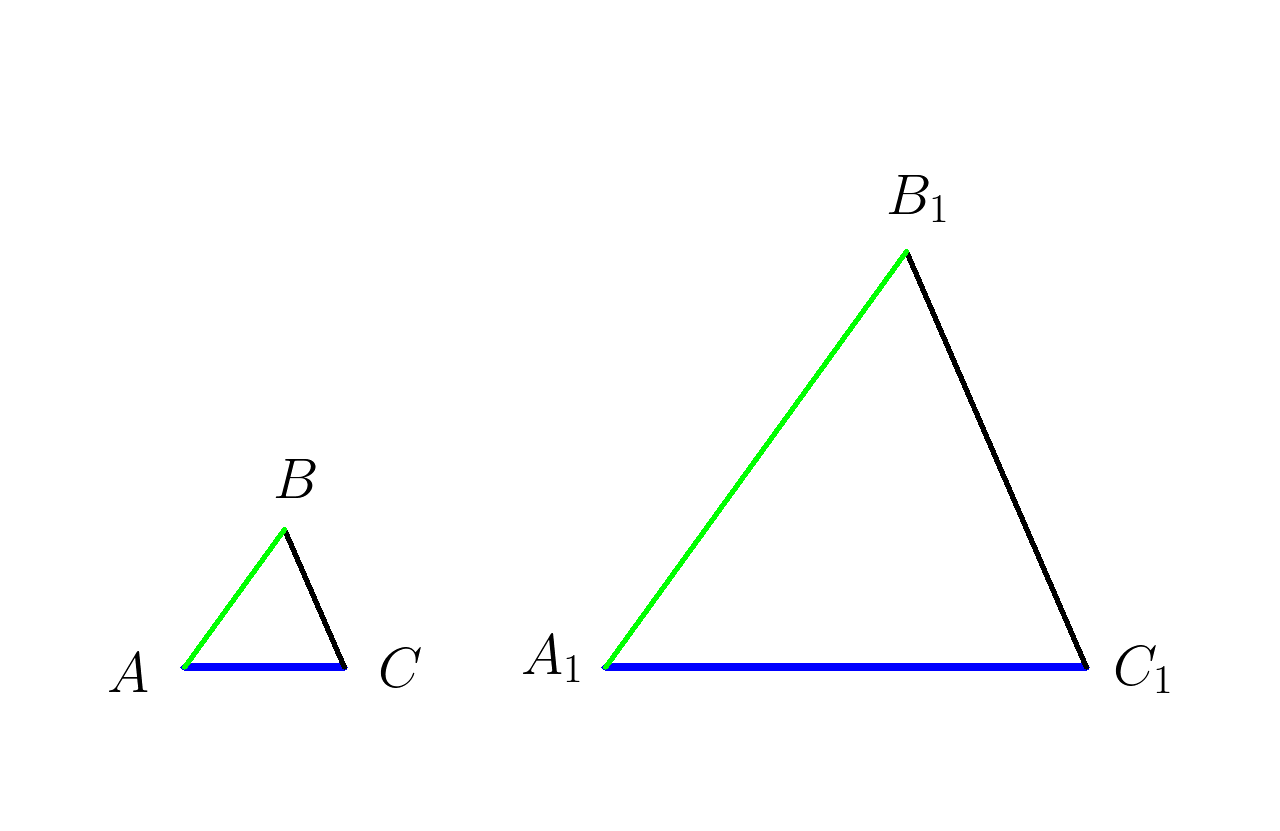
3. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=5, \; A_1B_1=15 , \; BC=4 . \) Найти \(B_1C_1 \)
Показать ответ
Показать решение
Видеорешение
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( \angle A=\angle A_1, \; \) значит \( BC и B_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{15}{5}=\dfrac{B_1C_1}{4} \)
\( B_1C_1 =12 \)
Ответ: \( B_1C_1 =12 \)
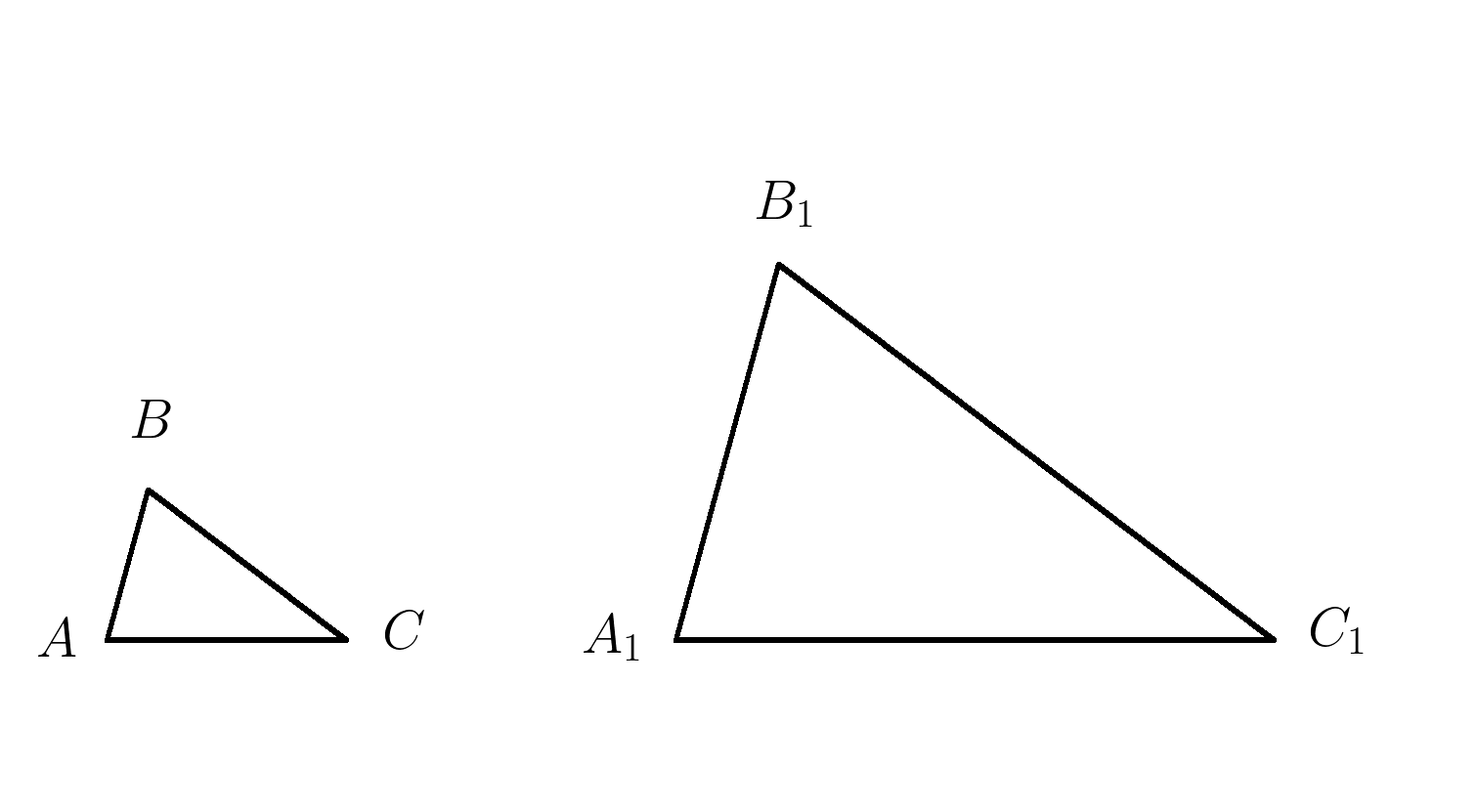
4. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=4, \; A_1B_1=10 , \; BC=8 . \) Найти \(B_1C_1 \)
Показать ответ
Показать решение
Видеорешение
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( \angle A=\angle A_1, \; \) значит \( BC и B_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{10}{4}=\dfrac{B_1C_1}{8} \)
\( B_1C_1 =20 \)
Ответ: \( B_1C_1 =20 \)
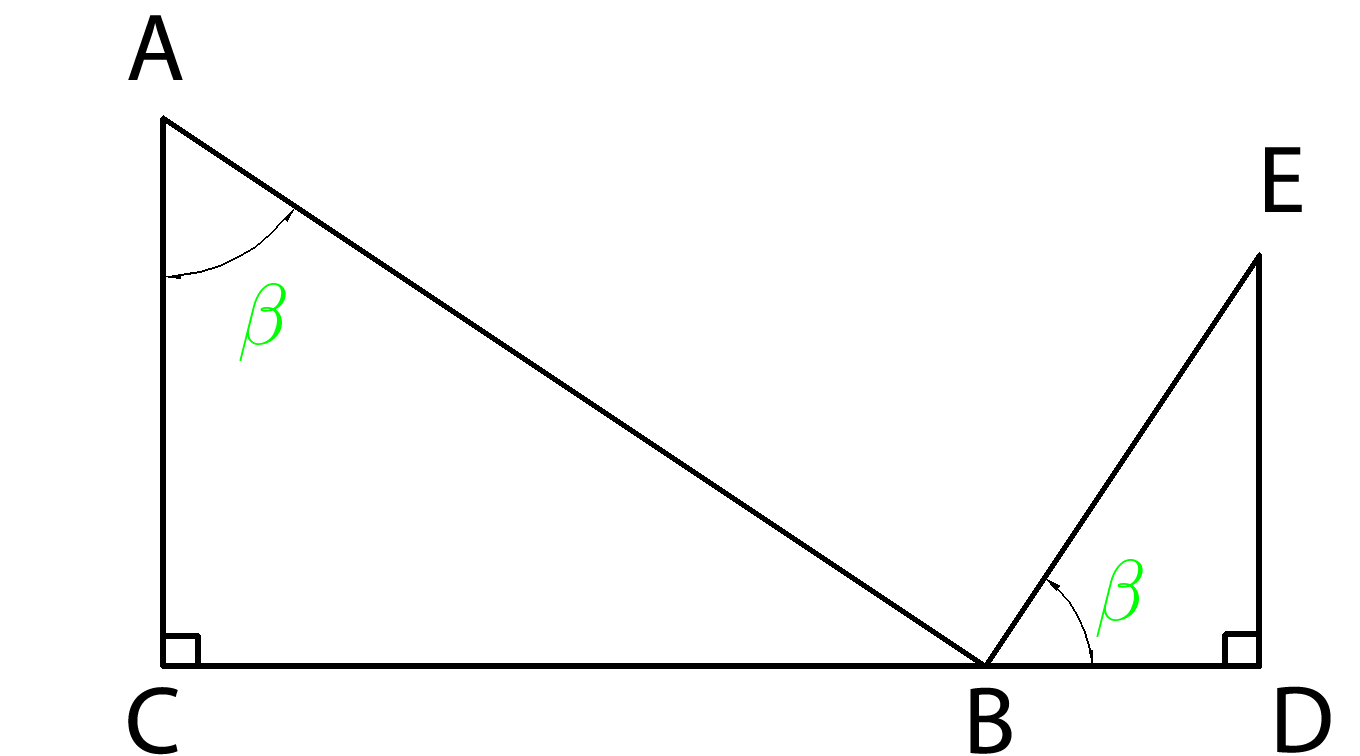
5. В прямоугольных треугольниках \(ABC \) и \(BED \ \angle A = \angle DBE={\color{Green} \beta} \) , а углы
\(C\) и \(D\) прямые. \(CB=120 , \ BE=100, \ DE=60 . \) Найдите \(AB\)
Показать ответ
Показать решение
Видеорешение
\( \Delta ABC ∾ \Delta BED \;\; \) (по двум углам)
\( BC \) лежит против \( {\color{Green} \beta} \),
\( ED \) лежит против \( {\color{Green} \beta} \),
значит \( BC \ и \ ED \) сходственные
\( AB \) лежит против прямого угла \(C \)
\( BE \) лежит против прямого угла \(D \)
значит \( AB \ и \ BE \) сходственные
\( \dfrac{BC}{ED}=\dfrac{AB}{BE} \)
\( \dfrac{120}{60}=\dfrac{AB}{100} \)
\( AB =200 \)
Ответ: \( AB =200 \)
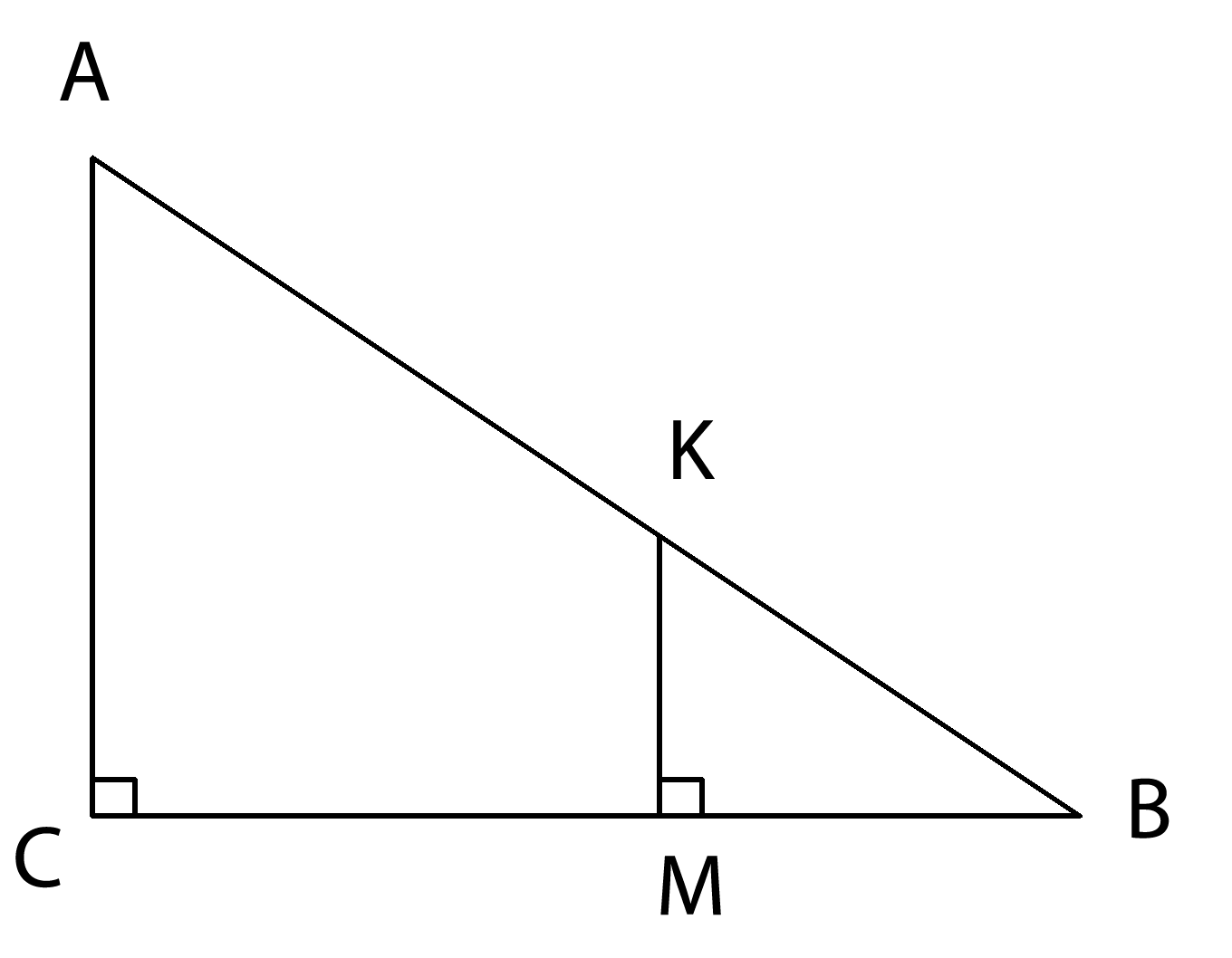
6. В прямоугольном треугольнике \(ABC \) через стороны \(AB \) и \(BC \) проводят отрезок
\(KM, \) параллельно стороне \(AC . \)
Известно, что \(KM=4, \ AC=10, \ MB=5 . \) Найти сторону \( BC. \)
Показать ответ
Показать решение
Видеорешение
\( \angle C=\angle M =90^0 \)
\( \angle B \) Общий
\( \Rightarrow \Delta ABC ∾ \Delta KMB \;\; \) (по двум углам)
Стороны \(AC \) и \( KM \) лежат против угла \(B \) , поэтому они являются сходственными
\( \angle A=\angle MKB \)
Сторона \( BC \) лежит против угла \(A\)
Сторона \( BM \) лежит против угла \( MKB \)
Значит стороны \( BC \) и \( BM \) сходственные
Запишем отношения подобия, будем делить стороны большого треугольника на стороны маленького:
\( \dfrac{AC}{KM}=\dfrac{BC}{BM} \)
\( \dfrac{10}{4}=\dfrac{BC}{5} \)
\(2,5=\dfrac{BC}{5} \)
\(\dfrac{BC}{5}=2,5 \)
\(BC=2,5 \cdot 5 \)
\( BC=12,5 \)
Ответ: \( BC=12,5 \)

7. В прямоугольном треугольнике \(ABC \) через стороны \(AB \) и \(BC \) проводят отрезок
\(KM, \) параллельно стороне \(AC . \)
Известно, что \(KM=5, \ AC=13, \ CM=9 . \) Найти \( BM. \)
Показать ответ
Показать решение
Видеорешение
\( \angle C=\angle M =90^0 \)
\( \angle B \) Общий
\( \Rightarrow \Delta ABC ∾ \Delta KMB \;\; \) (по двум углам)
Стороны \(AC \) и \( KM \) лежат против угла \(B \) , поэтому они являются сходственными
\( \angle A=\angle MKB \)
Сторона \( BC \) лежит против угла \(A\)
Сторона \( BM \) лежит против угла \( MKB \)
Значит стороны \( BC \) и \( BM \) сходственные
Запишем отношения подобия, будем делить стороны большого треугольника на стороны маленького:
\( \dfrac{AC}{KM}=\dfrac{BC}{BM} \)
\( \dfrac{AC}{KM}=\dfrac{CM+BM}{BM} \)
\( \dfrac{13}{5}=\dfrac{9+BM}{BM} \)
\(2,6=\dfrac{9+BM}{BM} \)
\(2,6BM=9+BM \)
\( 2,6BM-BM =9 \)
\( 1,6BM =9 \)
\( BM =9:1,6 \)
\( BM =5,625 \)
Ответ: \( BM =5,625 \)







