
1. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( cos\;A=\dfrac{3}{5}, \;\;AC=10 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение
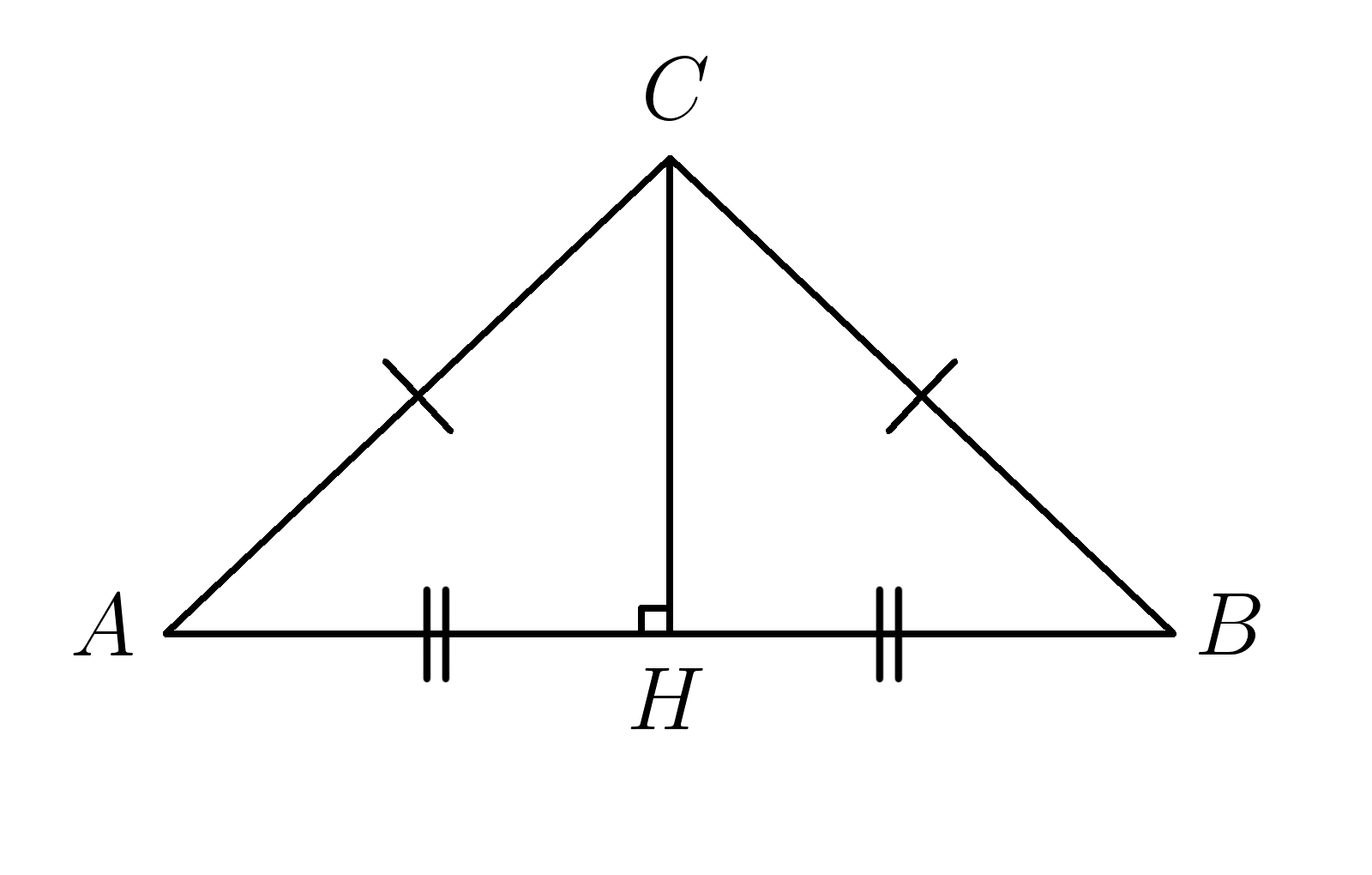
Проведем высоту \( CH \) для того чтобы мы смогли применить косинус
\( cos\;A=\dfrac{AH}{AC} \;\;\;\;\;\;\;\;\;\;\;\;\;cos\;A=\dfrac{3}{5} \)
\(\dfrac{AH}{10}=\dfrac{3}{5} \)
\( AH=6; \;\;\;\;\;\;\;\;\;\; AB=12 \)
Ответ: \( AB=12 \)

2. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( cos\;A=\dfrac{1}{10}, \;\;AC=9,5 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) для того чтобы мы смогли применить косинус
\( cos\;A=\dfrac{AH}{AC} \;\;\;\;\;\;\;\;\;\;\;\;\;cos\;A=\dfrac{1}{10} \)
\(\dfrac{AH}{9,5}=\dfrac{1}{10} \)
\( AH=0,95; \;\;\;\;\;\;\;\;\;\; AB=1,9 \)
Ответ: \( AB=1,9 \)

3. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( cos\;A=0,9\;, \;\;AC=0,05 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) для того чтобы мы смогли применить косинус
\( cos\;A=\dfrac{AH}{AC} \;\;\;\;\;\;\;\;\;\;\;\;\;cos\;A=0,9 \)
\(\dfrac{AH}{0,05}=0,9 \)
\( AH=0,045; \;\;\;\;\;\;\;\;\;\; AB=0,09\)
Ответ: \( AB=0,09 \)

4. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( sin\;A=\dfrac{\sqrt{3}}{2}\;, \;\;AC=5 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) и увидим что нам нужен косинус
\( cos\;A=\dfrac{AH}{5} \)
Найдем косинус из основного тригонометрического тождества:
\(sin^2\;A+cos^2\;A=1 \)
\((\dfrac{\sqrt{3}}{2})^2+cos^2\;A=1 \)
\(cos^2\;A=1-\dfrac{3}{4} \)
\(cos^2\;A=\dfrac{1}{4} \)
\(cos\;A=\dfrac{1}{2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; cos\;A=-\dfrac{1}{2} \)
Угол A острый, поэтому \(cos\;A=\dfrac{1}{2} \)
\(\dfrac{1}{2}=\dfrac{AH}{5} \)
\(AH=2,5 \)
\(AB=5 \)
Ответ: \(AB=5 \)

5. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( sin\;A=\sqrt{\dfrac{69}{71}}\;, \;\;AC=\sqrt{142} \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) и увидим что нам нужен косинус
\( cos\;A=\dfrac{AH}{\sqrt{142}} \)
Найдем косинус из основного тригонометрического тождества:
\(sin^2\;A+cos^2\;A=1 \)
\((\sqrt{\dfrac{69}{71}})^2+cos^2\;A=1 \)
\(cos^2\;A=1-\dfrac{69}{71} \)
\(cos^2\;A=\dfrac{2}{71} \)
\(cos\;A=\dfrac{\sqrt{2}}{\sqrt{71}} \;\;\;\;\;\;\;или\;\;\;\;\;\;\;\; cos\;A=- \dfrac{\sqrt{2}}{\sqrt{71}} \)
Угол A острый, поэтому \(cos\;A=\dfrac{\sqrt{2}}{\sqrt{71}} \)
\( \dfrac{\sqrt{2}}{\sqrt{71}}=\dfrac{AH}{\sqrt{142}} \)
\(AH=\dfrac{\sqrt{2}\cdot \sqrt{142}}{\sqrt{71}} \)
\(AH= \dfrac{\sqrt{2}\cdot \sqrt{2}\cdot \sqrt{71}}{\sqrt{71}}=2 \)
\(AB=4 \)
Ответ: \(AB=4 \)

6. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) .
\( sin\;A=\dfrac{\sqrt{19}}{10}\;, \;\;AC=0,05 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) и увидим что нам нужен косинус
\( cos\;A=\dfrac{AH}{0,05} \)
Найдем косинус из основного тригонометрического тождества:
\(sin^2\;A+cos^2\;A=1 \)
\( (\dfrac{\sqrt{19}}{10})^2+cos^2\;A=1 \)
\(cos^2\;A=1-\dfrac{19}{100} \)
\(cos^2\;A=\dfrac{81}{100} \)
\(cos\;A=\dfrac{9}{10} \;\;\;\;\;\;\;или\;\;\;\;\;\;\;\; cos\;A=-\dfrac{9}{10} \)
Угол A острый, поэтому \( cos\;A=\dfrac{9}{10}=0,9 \)
\(\dfrac{AH}{0,05}=0,9 \)
\( AH=0,045; \;\;\;\;\;\;\;\;\;\; AB=0,09\)
Ответ: \( AB=0,09 \)

7. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) .
\( tg\;B=\dfrac{\sqrt{13}}{2}\;, \;\;CB=5\sqrt{17} \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) и увидим что нам нужен косинус
\( cos\;B=\dfrac{HB}{5\sqrt{17}} \)
Найдем косинус из основного тригонометрического тождества:
Разделим основное тригонометрическое тождество на \( cos^2\;B \) :
\(sin^2 \;B+cos^2\;B=1\)
\( \dfrac{sin^2\;B}{cos^2\;B}+\dfrac{cos^2\;B}{cos^2\;B} = \dfrac{1}{cos^2\;B}\)
\(tg^2 \;B+1=\dfrac{1}{cos^2\;B} \)
\(cos^2\;B \cdot ( tg^2 \;B+1)=1 \)
\(cos^2\;B =\dfrac{1}{tg^2\;B+1} \)
\(cos\;B =+\sqrt{\dfrac{1}{tg^2\;B+1}} \;\;\;\;\;\;\;так\;как\;угол\;B\; острый \)
\(cos\;B =\sqrt{\dfrac{1}{(\dfrac{\sqrt{13}}{2})^2+1}}=\sqrt{\dfrac{\;\;\;1\;\;\;}{\dfrac{13}{4}+1}}=
\sqrt{\dfrac{\;\;\;1\;\;\;}{(\dfrac{17}{4})}} = \sqrt{\dfrac{\;\;\;4\;\;}{17}}=
\dfrac{2}{\sqrt{17}} \)
\( \dfrac{HB}{5\sqrt{17}}=\dfrac{2}{\sqrt{17}} \)
\( HB=10; \;\;\;\;\;\;\;\;\;\; AB=20\)
Ответ: \( AB=20 \)

8. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) .
\( tg\;B=2\sqrt{19}\;, \;\;CB=13\sqrt{77} \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение

Проведем высоту \( CH \) и увидим что нам нужен косинус
\( cos\;B=\dfrac{HB}{13\sqrt{77}} \)
Найдем косинус из основного тригонометрического тождества:
Разделим основное тригонометрическое тождество на \( cos^2\;B \) :
\(sin^2 \;B+cos^2\;B=1\)
\( \dfrac{sin^2\;B}{cos^2\;B}+\dfrac{cos^2\;B}{cos^2\;B} = \dfrac{1}{cos^2\;B}\)
\(tg^2 \;B+1=\dfrac{1}{cos^2\;B} \)
\(cos^2\;B \cdot ( tg^2 \;B+1)=1 \)
\(cos^2\;B =\dfrac{1}{tg^2\;B+1} \)
\(cos\;B =+\sqrt{\dfrac{1}{tg^2\;B+1}} \;\;\;\;\;\;\;так\;как\;угол\;B\; острый \)
\(cos\;B =\sqrt{\dfrac{1}{(2\sqrt{19})^2+1}}=\sqrt{\dfrac{\;\;\;1\;\;\;}{76+1}}=
\sqrt{\dfrac{\;\;\;1\;\;\;}{77}} = \dfrac{1}{\sqrt{77}} \)
\( \dfrac{HB}{13\sqrt{77}}=\dfrac{1}{\sqrt{77}} \)
\( HB=13; \;\;\;\;\;\;\;\;\;\; AB=26\)
Ответ: \( AB=26 \)

13. Треугольник \(ABC \) равнобедренный \( (AC=BC) \) .
\( sin\;B=\dfrac{5}{\sqrt{34}}\;, \;\;CH=45 \) . Найти \(AB \)
Показать ответ
Показать решение
Видеорешение
Сначала найдем \(CB\):
\( sin\;B=\dfrac{5}{\sqrt{34}}= \dfrac{45}{CB} \)
\( CB=9\sqrt{34} \)
а потом \(HB \) по теореме Пифагора:
\( 45^2+HB^2=(9\sqrt{34})^2 \)
\(HB^2=9^2\cdot \sqrt{34}^2 -45^2 \)
\(HB^2=81\cdot 34 -2025 \)
\(HB^2=2754 -2025 \)
\(HB^2=729 \)
\(HB=27 \)
\(AB=54 \)
Ответ: \(AB=54\)

1. Контрольный 99
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( cos\;A=\dfrac{1}{9\sqrt{43}}\;, \;\;AB=\dfrac{22}{\sqrt{43}} \) . Найти \(AC \)

2. Контрольный 6
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( cos\;A=\dfrac{33}{\sqrt{1331}}\;, \;\;AC=\sqrt{11} \) . Найти \(AB \)

3. Контрольный 70
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( sin\;A=\dfrac{2}{3}\;, \;\;AC=21\sqrt{5} \) . Найти \(AB \)

4. Контрольный 0,625
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( sin\;A=\dfrac{9}{16}\;, \;\;AC=\dfrac{1}{\sqrt{7}} \) . Найти \(AB \)

5. Контрольный 46
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( sin\;B=\dfrac{11}{12}\;, \;\;AC=\sqrt{3312} \) . Найти \(AB \)

6. Контрольный 48
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( tg\;B=\dfrac{2\sqrt{5}}{3}\;, \;\;AC=8\sqrt{29} \) . Найти \(AB \)

7. Контрольный 2
Треугольник \(ABC \) равнобедренный \( (AC=BC) \) . \( tg\;B=\dfrac{\sqrt{101}}{32}\;, \;\;AC=\dfrac{15\sqrt{5}}{32} \) . Найти \(AB \)
|















