Синус, косинус и тангенс

Репетитор
по физике

916 478 1032

П
Р
О
Г
Р
А
М
М
И
Р
О
В
А
Н
И
Е
Репетитор
916 478 1032

Репетитор
по физике

916 478 1032

Репетитор
по алгебре

916 478 1032

Репетитор
по физике

916 478 1032

Синус, косинус и тангенс .

Синусом угла в прямоугольном треугольнике называют отношение (деление) противолежащего катета на гипотенузу

Косинусом угла в прямоугольном треугольнике называют отношение (деление) прилежащего катета на гипотенузу

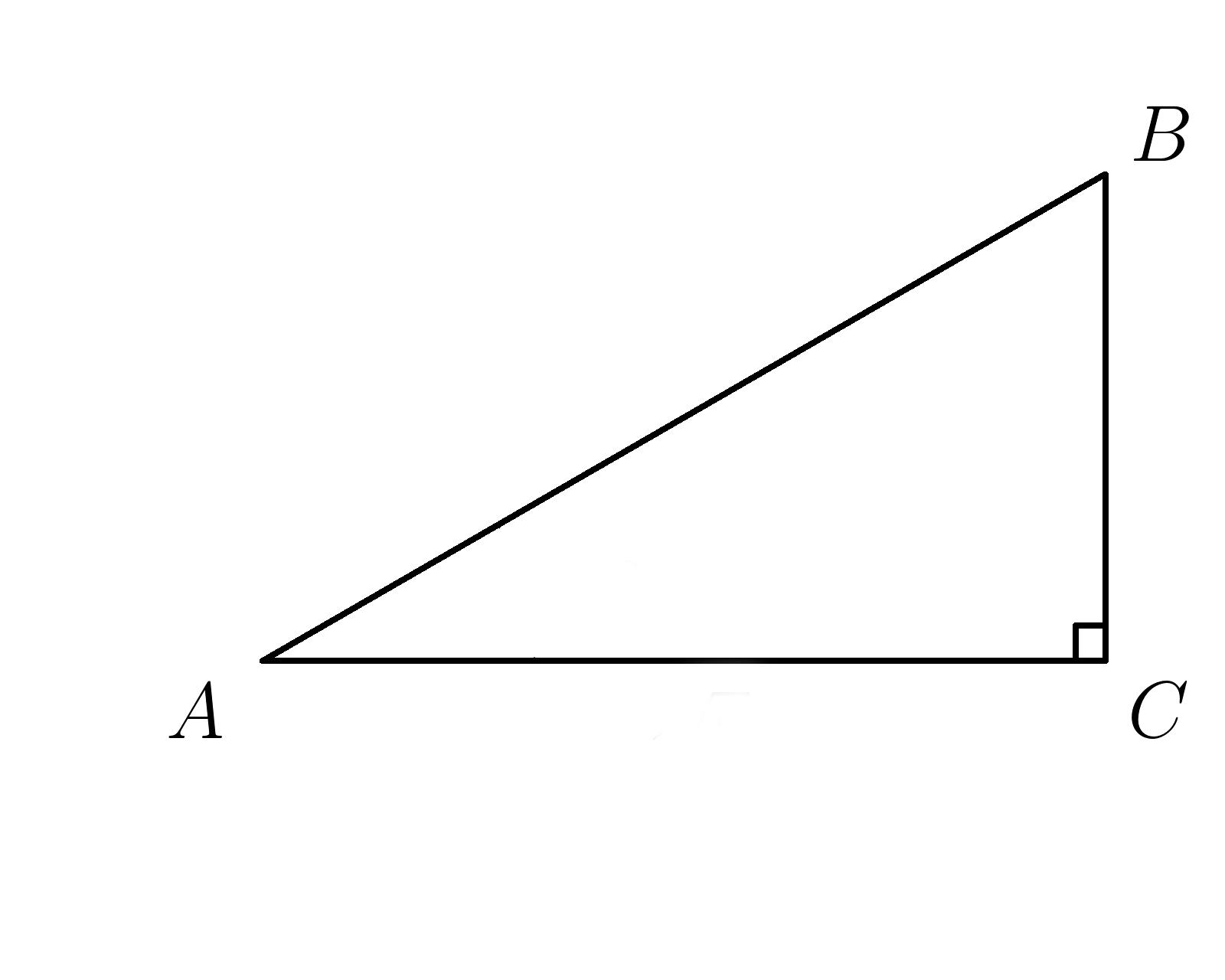s i n A = \frac{B C}{A B}

c o s A = \frac{A C}{A B}

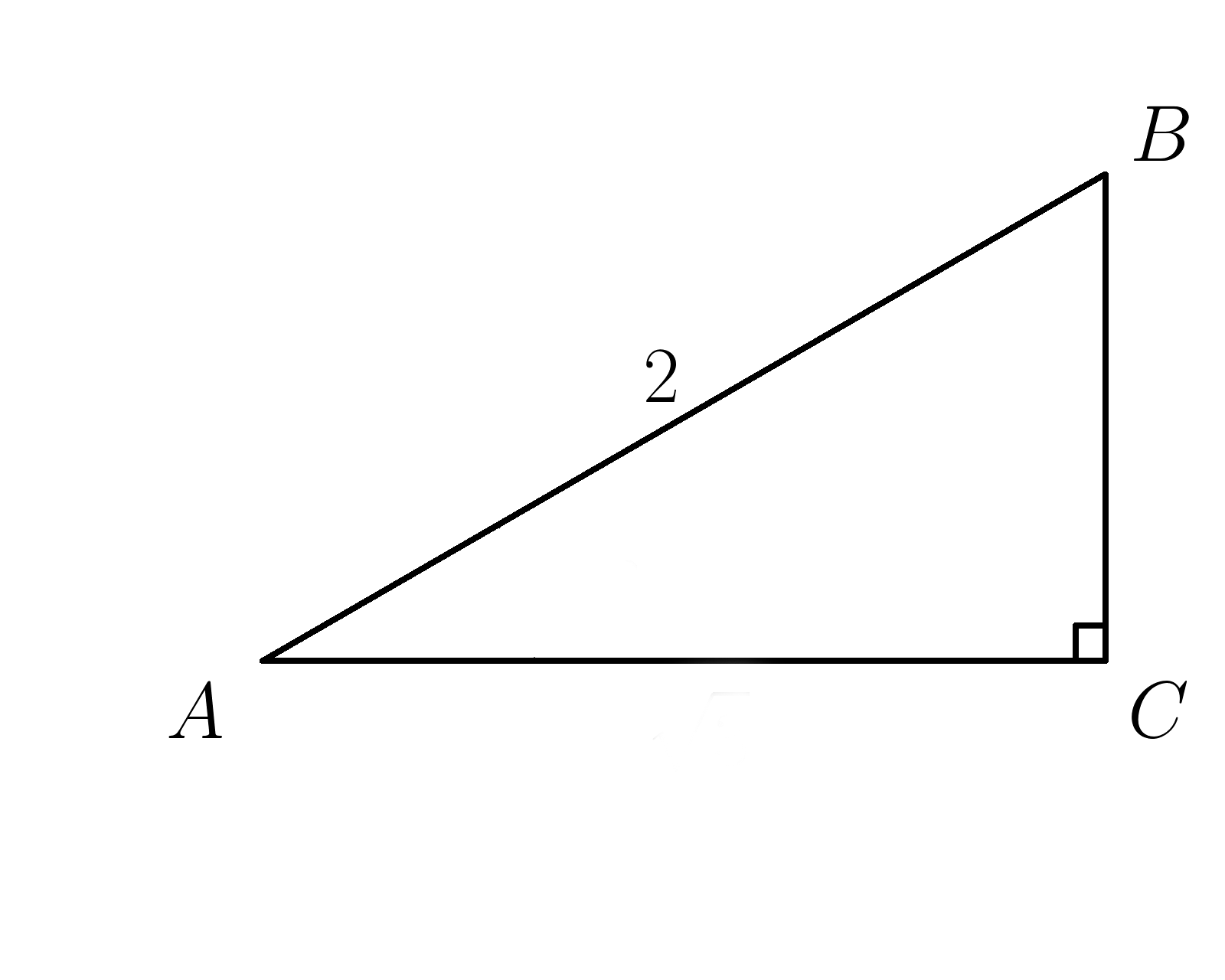
1. Гипотенуза $A B = 2$ , а синус угла $A$ равен $\frac{1}{2}$ . Найти катет $B C$
Показать ответ Показать решение Видеорешение

Ответ: $B C = 1$

$s i n A = \frac{1}{2}$

$s i n A = \frac{B C}{A B}$

$\frac{1}{2} = \frac{B C}{2}$

$\frac{1}{2} \cdot 2 = \frac{B C}{2} \cdot 2$

$1 = B C$

$B C = 1$

Ответ: $B C = 1$

ПОЗЖЕ

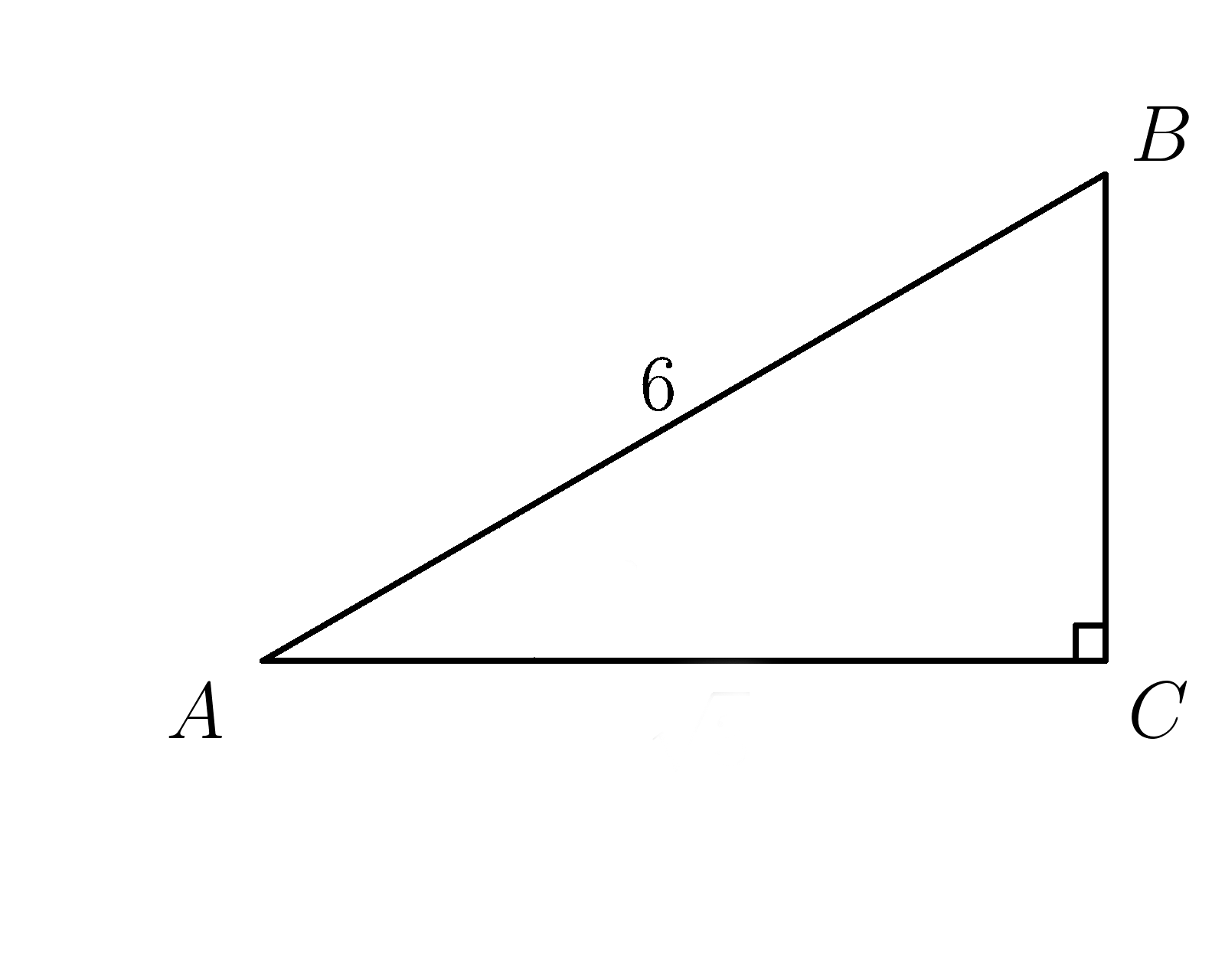
2. Гипотенуза $A B = 6, s i n A = \frac{2}{3}$ . Найти катет $B C$
Показать ответ Показать решение Видеорешение


Ответ: $B C = 4$

$s i n A = \frac{2}{3}$

$s i n A = \frac{B C}{A B}$

$\frac{2}{3} = \frac{B C}{6}$

$\frac{2}{3} \cdot 6 = \frac{B C}{6} \cdot 6$

$4 = B C$

$B C = 4$

Ответ: $B C = 4$

ПОЗЖЕ

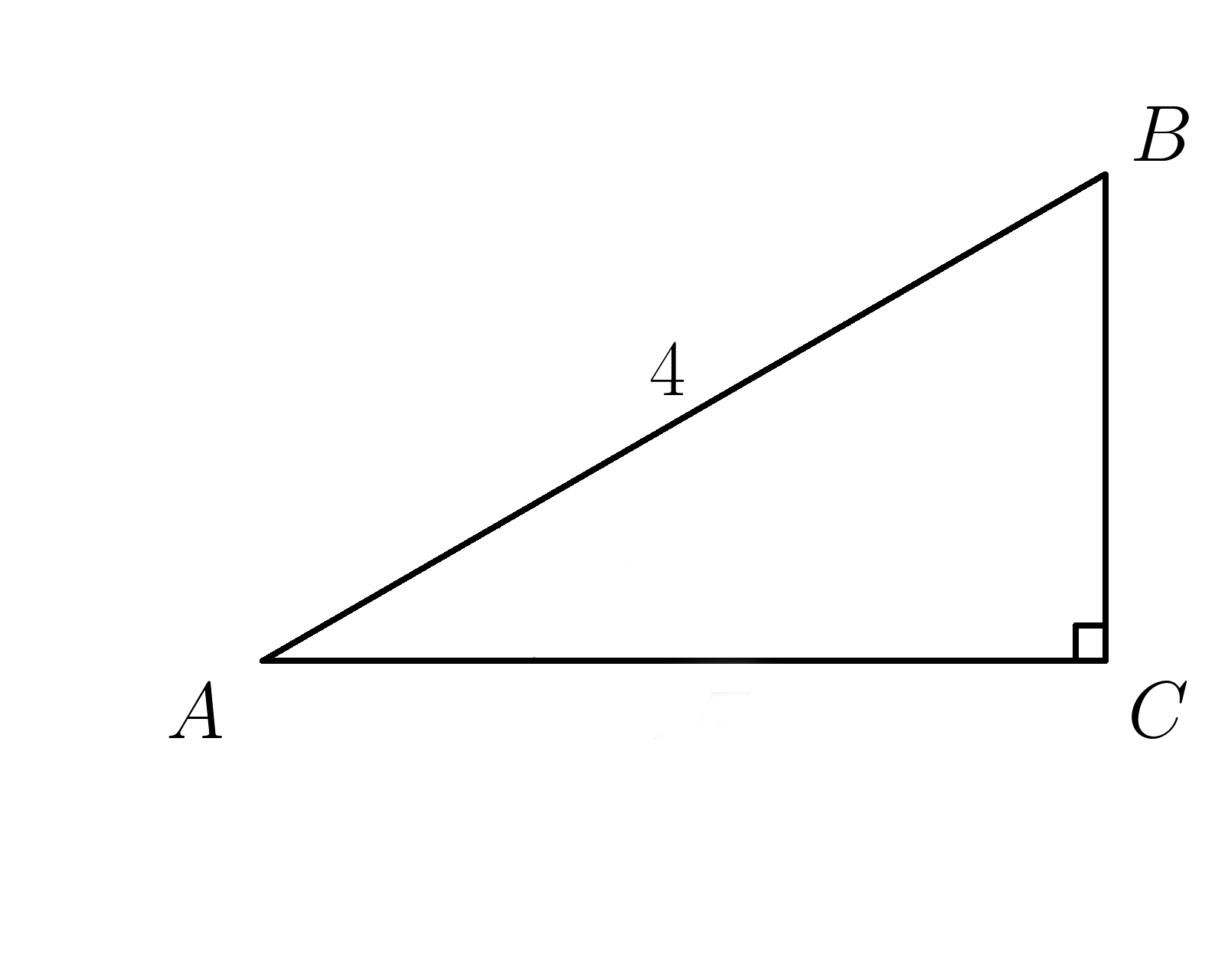
3. Гипотенуза $A B = 4, s i n A = \frac{3}{4}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


Ответ: $B C = 3$

$s i n A = \frac{3}{4}$

$s i n A = \frac{B C}{A B}$

$\frac{3}{4} = \frac{B C}{4}$

$\frac{3}{4} \cdot 4 = \frac{B C}{4} \cdot 4$

$3 = B C$

$B C = 3$

Ответ: $B C = 3$

Решить легкую контрольную работу по теме "Определение синуса, косинуса и тангенса"

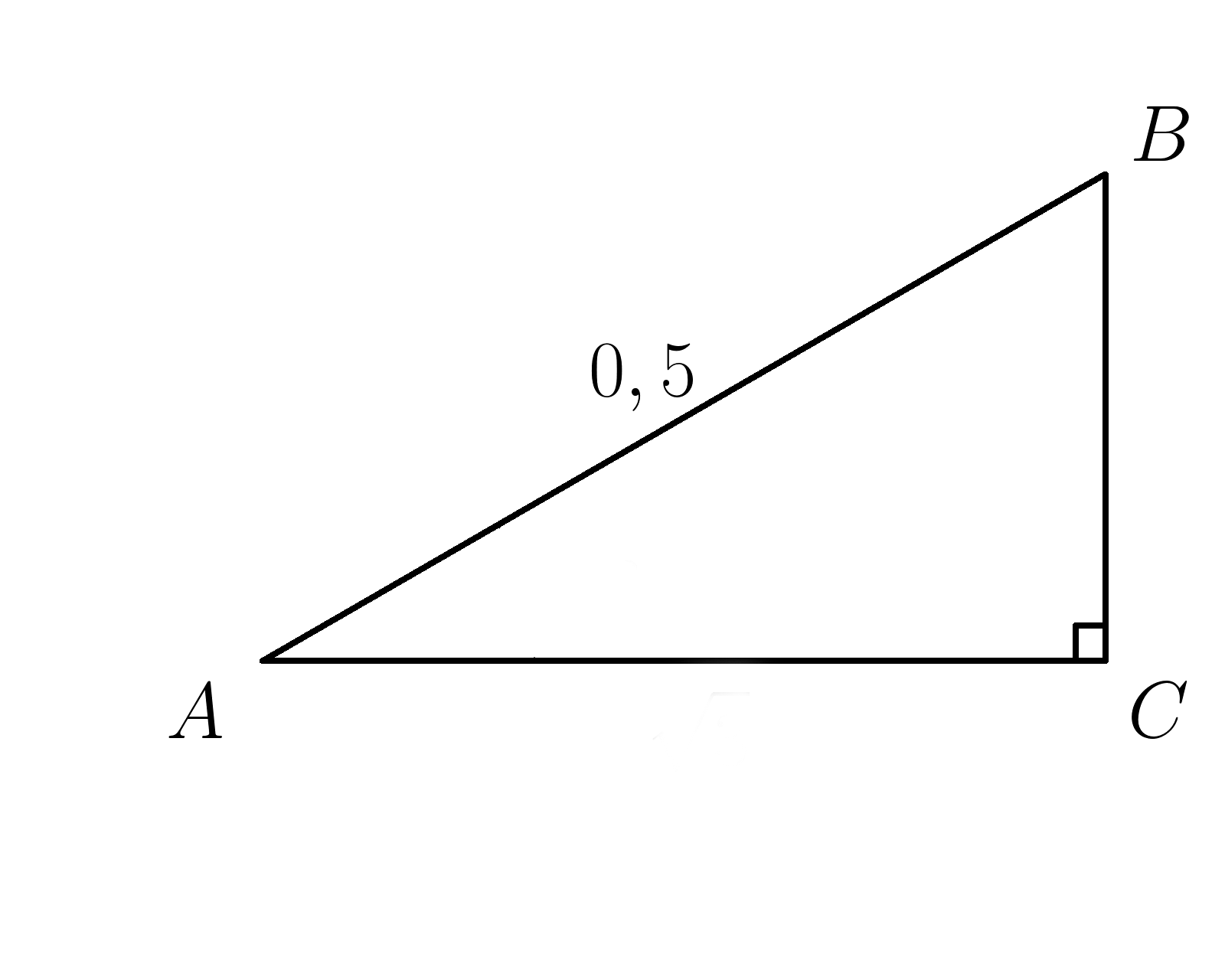
4. Гипотенуза $A B = 0, 5 . s i n A = \frac{2}{5}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


Ответ: $B C = 0, 2$

$s i n A = \frac{2}{5}$

$s i n A = \frac{B C}{A B}$

$\frac{2}{5} = \frac{B C}{0, 5}$

$\frac{2}{5} \cdot 0, 5 = \frac{B C}{0, 5} \cdot 0, 5$

$\frac{1}{5} = B C$

$B C = \frac{1}{5} = 0, 2$

Ответ: $B C = 0, 2$

ПОЗЖЕ

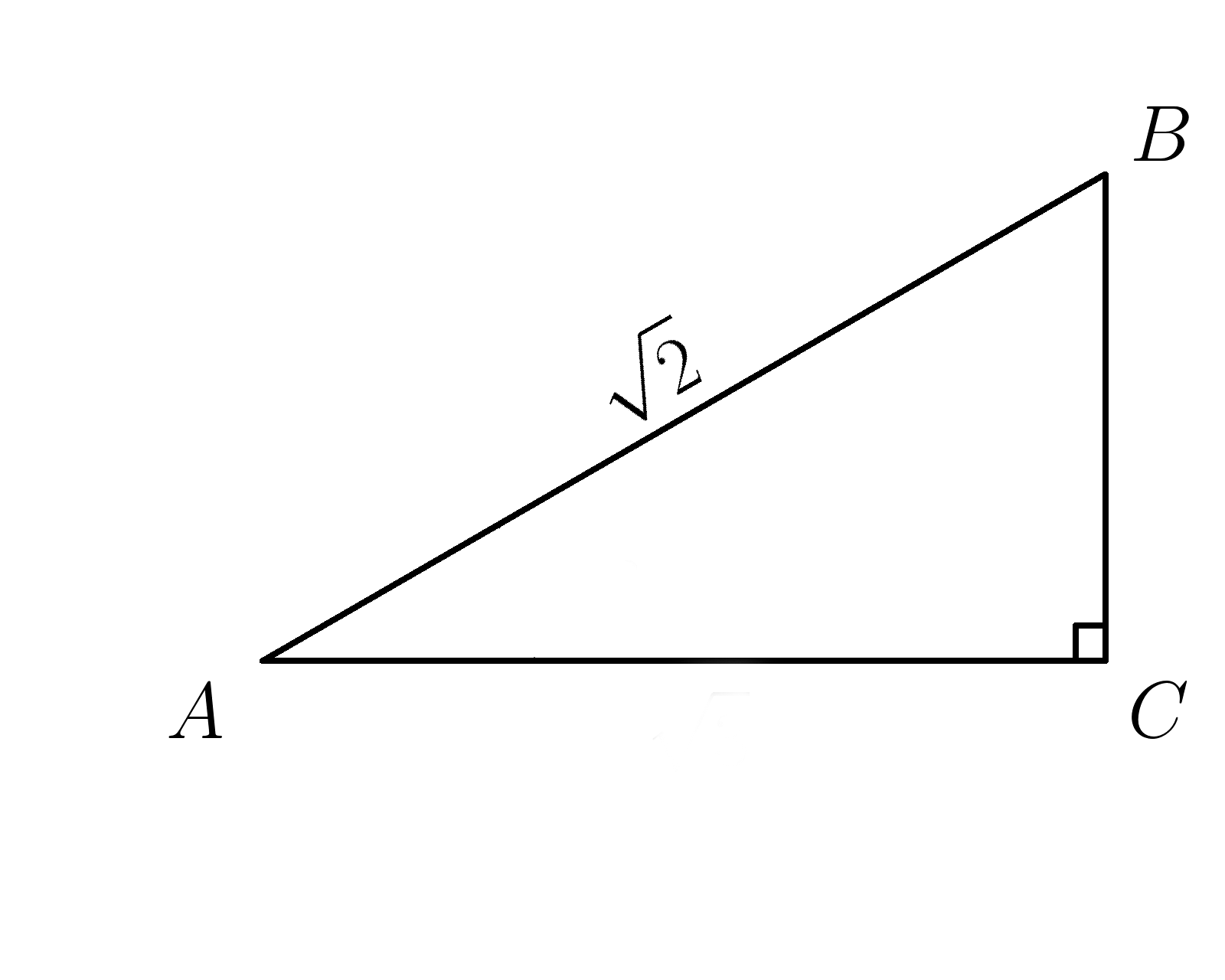
5. Гипотенуза $A B = \sqrt{2}, s i n A = \frac{\sqrt{2}}{2}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


Ответ: $B C = 1$

$s i n A = \frac{\sqrt{2}}{2}$

$s i n A = \frac{B C}{A B}$

$\frac{\sqrt{2}}{2} = \frac{B C}{\sqrt{2}}$

$\frac{\sqrt{2}}{2} \cdot \sqrt{2} = \frac{B C}{\sqrt{2}} \cdot \sqrt{2}$

$1 = B C$

$B C = 1$

Ответ: $B C = 1$

ПОЗЖЕ

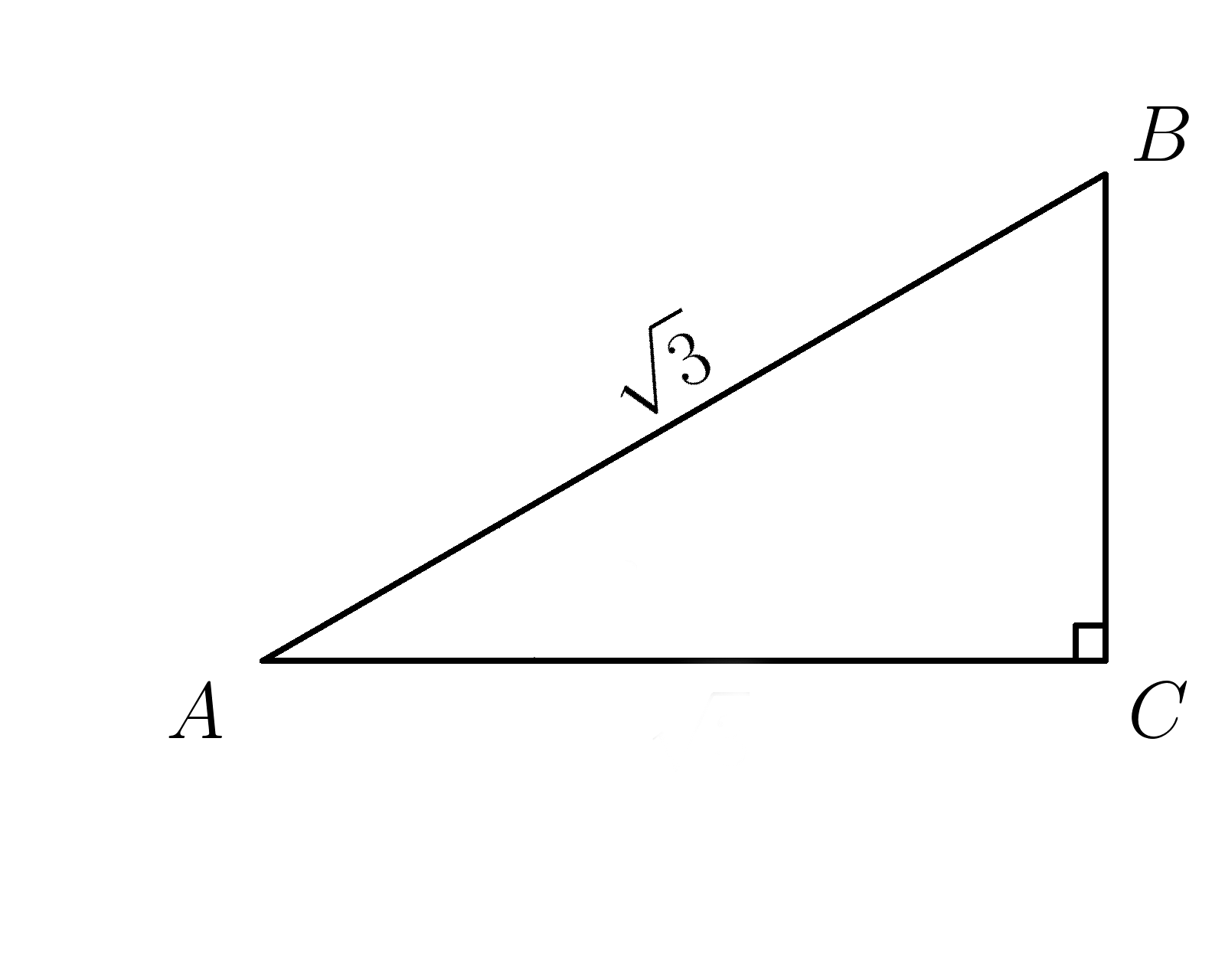
6. Гипотенуза $A B = \sqrt{3}, s i n A = \frac{\sqrt{3}}{2}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


$B C = 1, 5$

$s i n A = \frac{\sqrt{3}}{2}$

$s i n A = \frac{B C}{A B}$

$\frac{\sqrt{3}}{2} = \frac{B C}{\sqrt{3}}$

$\frac{\sqrt{3}}{2} \cdot \sqrt{3} = \frac{B C}{\sqrt{3}} \cdot \sqrt{3}$

$\frac{3}{2} = B C$

$B C = 1, 5$

Ответ: $B C = 1, 5$

ПОЗЖЕ

7. Гипотенуза $A B = \sqrt{3}, s i n A = \frac{2}{3}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


$\frac{2 \sqrt{3}}{3}$

$s i n A = \frac{2}{3}$

$s i n A = \frac{B C}{A B}$

$\frac{2}{3} = \frac{B C}{\sqrt{3}}$

$\frac{2}{3} \cdot \sqrt{3} = \frac{B C}{\sqrt{3}} \cdot \sqrt{3}$

$\frac{2 \sqrt{3}}{3} = B C$

$B C = \frac{2 \sqrt{3}}{3}$

Ответ: $B C = \frac{2 \sqrt{3}}{3}$

ПОЗЖЕ

8. Гипотенуза $A B = \sqrt{2}, s i n A = \frac{\sqrt{8}}{10}$ . Найти $B C$ .
Показать ответ Показать решение Видеорешение


Ответ: $B C = 0, 4$

$s i n A = \frac{\sqrt{8}}{10} s i n A = \frac{B C}{A B}$

$\frac{B C}{\sqrt{2}} = \frac{\sqrt{8}}{10}$

$\frac{B C}{\sqrt{2}} \cdot \sqrt{2} = \frac{\sqrt{8}}{10} \cdot \sqrt{2}$

$B C = \frac{\sqrt{16}}{10}$

$B C = \frac{4}{10} = 0, 4$

Ответ: $B C = 0, 4$

ПОЗЖЕ

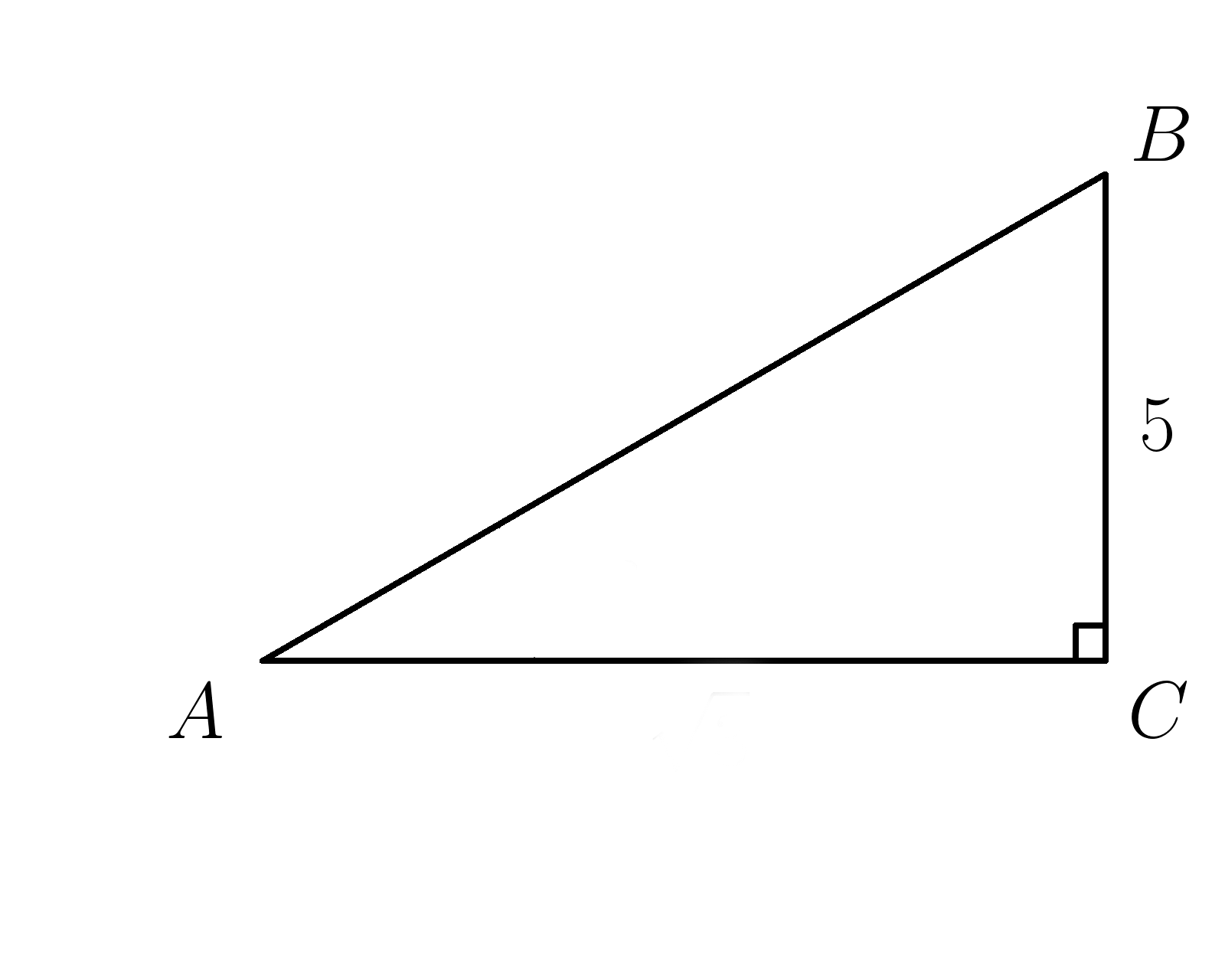
9. Катет $B C = 5, s i n A = \frac{1}{2}$ . Найти гипотенузу $A B$ .
Показать ответ Показать решение Видеорешение


$A B = 10$

$s i n A = \frac{1}{2} s i n A = \frac{B C}{A B}$

$\frac{1}{2} = \frac{5}{A B}$

$\frac{1}{2} \cdot 2 A B = \frac{5}{A B} \cdot 2 A B$

$A B = 2 \cdot 5 = 10$

Ответ: $A B = 10$

ПОЗЖЕ

10. Катет $B C = 5, s i n A = \frac{2}{5}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 12, 5$

$s i n A = \frac{2}{5} s i n A = \frac{B C}{A B}$

$\frac{2}{5} = \frac{5}{A B}$

$\frac{2}{5} \cdot 5 A B = \frac{5}{A B} \cdot 5 A B$

$2 \cdot A B = 5 \cdot 5$

$A B = 12, 5$

Ответ: $A B = 12, 5$

ПОЗЖЕ

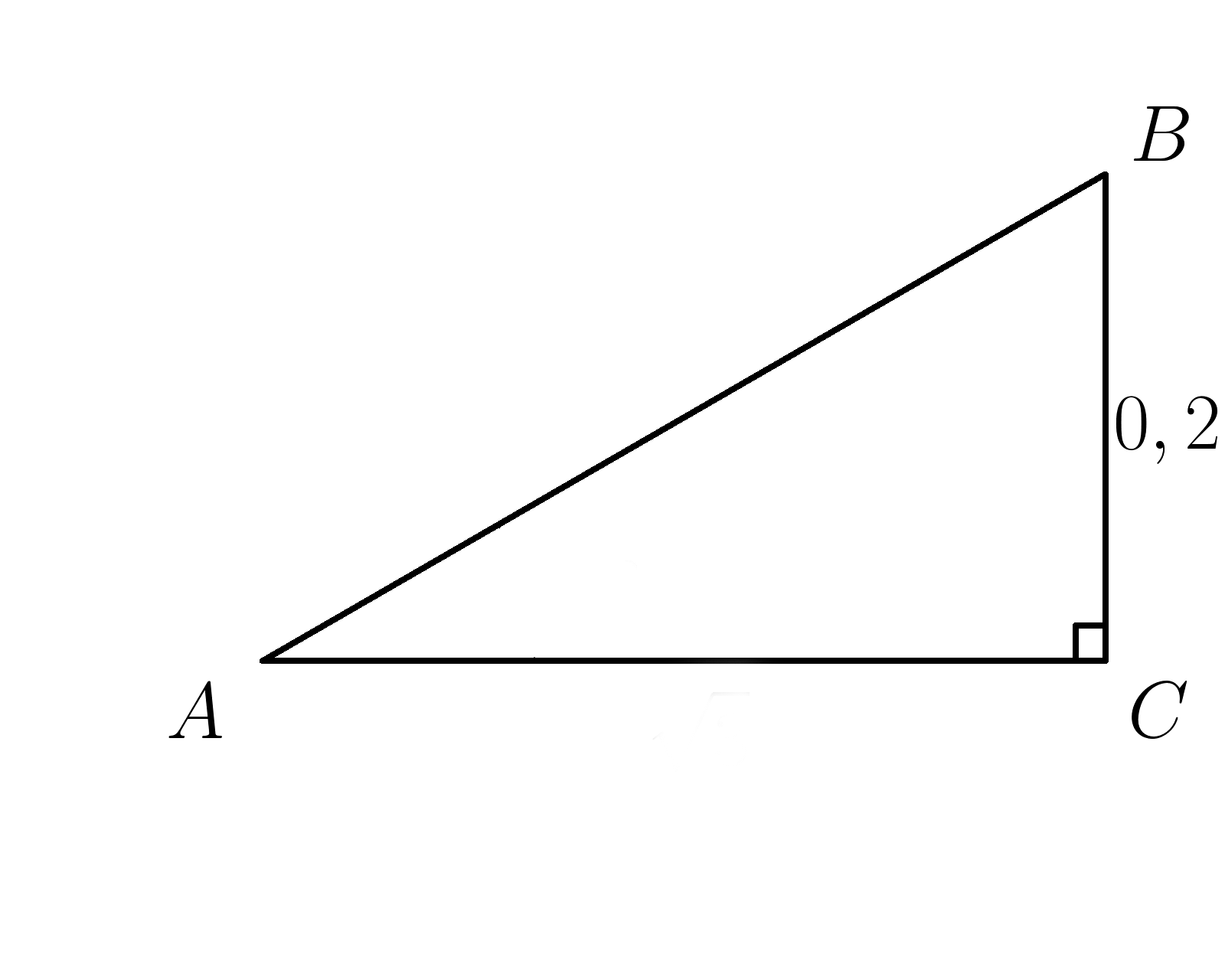
11. Катет $B C = 0, 2 . s i n A = \frac{2}{7}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 0, 7$

$s i n A = \frac{2}{7} s i n A = \frac{B C}{A B}$

$\frac{2}{7} = \frac{0, 2}{A B}$

$\frac{2}{7} \cdot 7 A B = \frac{0, 2}{A B} \cdot 7 A B$

$2 \cdot A B = 7 \cdot 0, 2$

$A B = 0, 7$

Ответ: $A B = 0, 7$

ПОЗЖЕ

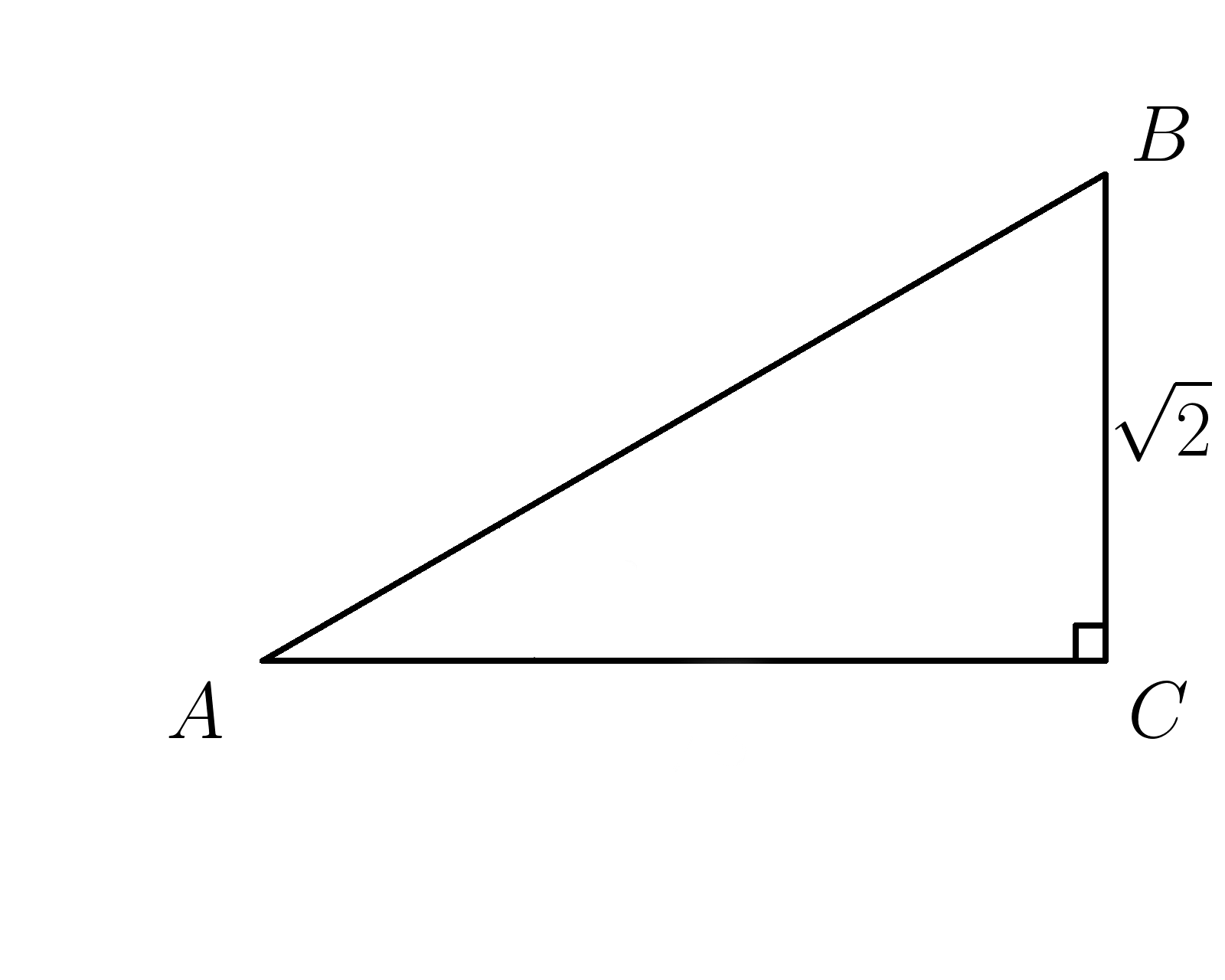
12. Катет $B C = \sqrt{2} . s i n A = \frac{\sqrt{2}}{2}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 2$

$s i n A = \frac{\sqrt{2}}{2} s i n A = \frac{B C}{A B}$

$\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{A B}$

$\frac{\sqrt{2}}{2} \cdot 2 A B = \frac{\sqrt{2}}{A B} \cdot 2 A B$

$\sqrt{2} \cdot A B = 2 \cdot \sqrt{2}$

$A B = 2$

Ответ: $A B = 2$

ПОЗЖЕ

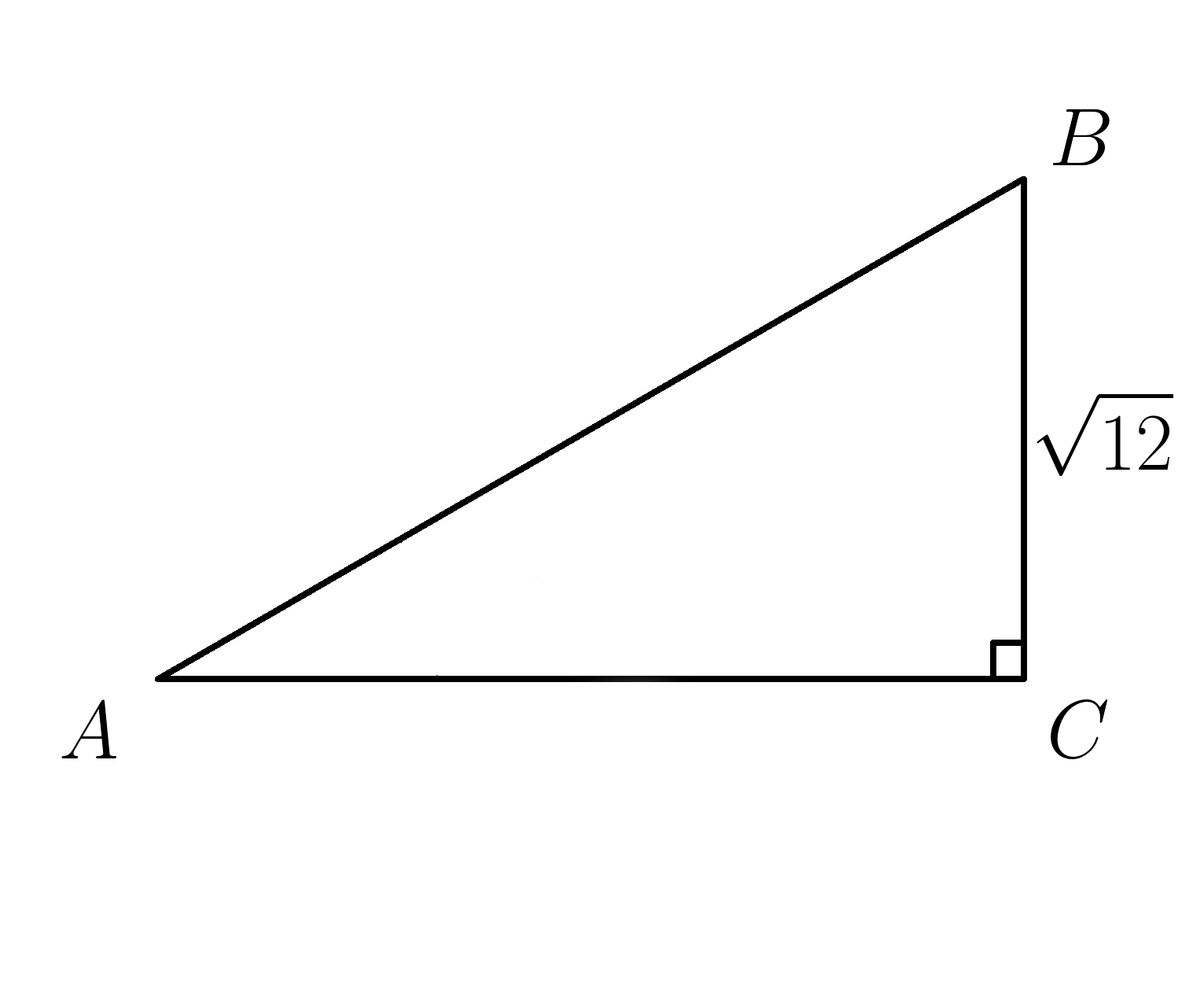
13. Катет $B C = \sqrt{12} . s i n A = \frac{\sqrt{3}}{2}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 4$

$s i n A = \frac{\sqrt{3}}{2} s i n A = \frac{B C}{A B}$

$\frac{\sqrt{3}}{2} = \frac{\sqrt{12}}{A B}$

$\sqrt{3} \cdot A B = 2 \cdot \sqrt{12}$

$A B = \frac{2 \sqrt{12}}{\sqrt{3}}$

$A B = 4$

Ответ: $A B = 4$

ПОЗЖЕ

14. Гипотенуза $A B = 2$ , а косинус угла $A$ равен $\frac{1}{2}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 1$

$c o s A = \frac{1}{2} c o s A = \frac{A C}{A B}$

$\frac{A C}{2} = \frac{1}{2}$

$A C = 1$

Ответ: $A C = 1$

ПОЗЖЕ

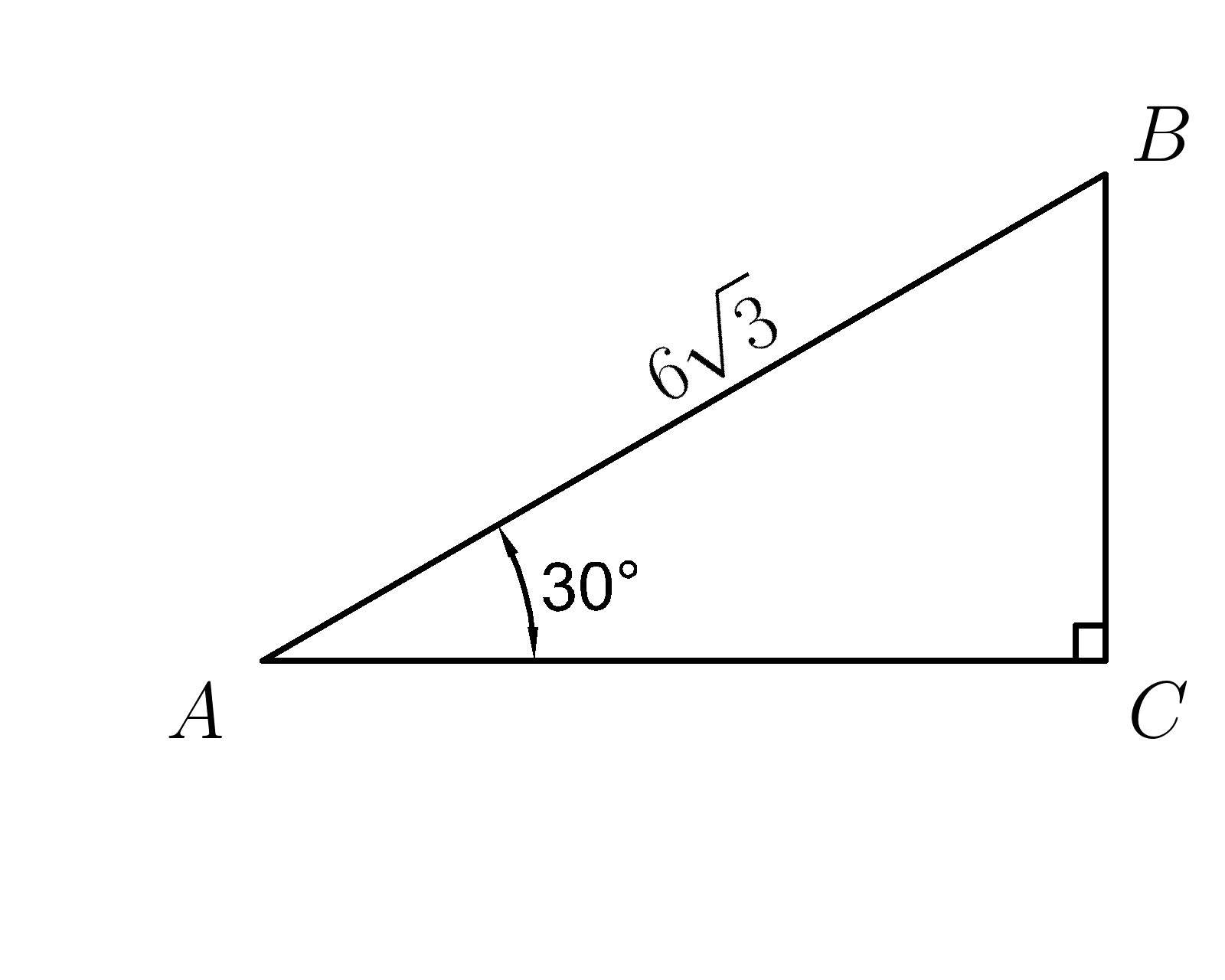
15. Гипотенуза $A B = 6 \sqrt{3}, ∡ B A C = 30^{0}, c o s 30^{0} = \frac{\sqrt{3}}{2}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 9$

$c o s A = \frac{\sqrt{3}}{2} c o s A = \frac{A C}{A B}$

$\frac{A C}{6 \sqrt{3}} = \frac{\sqrt{3}}{2}$

$A C = \frac{6 \sqrt{3} \cdot \sqrt{3}}{2}$

$A C = \frac{6 \cdot 3}{2} = 9$

Ответ: $A C = 9$

ПОЗЖЕ

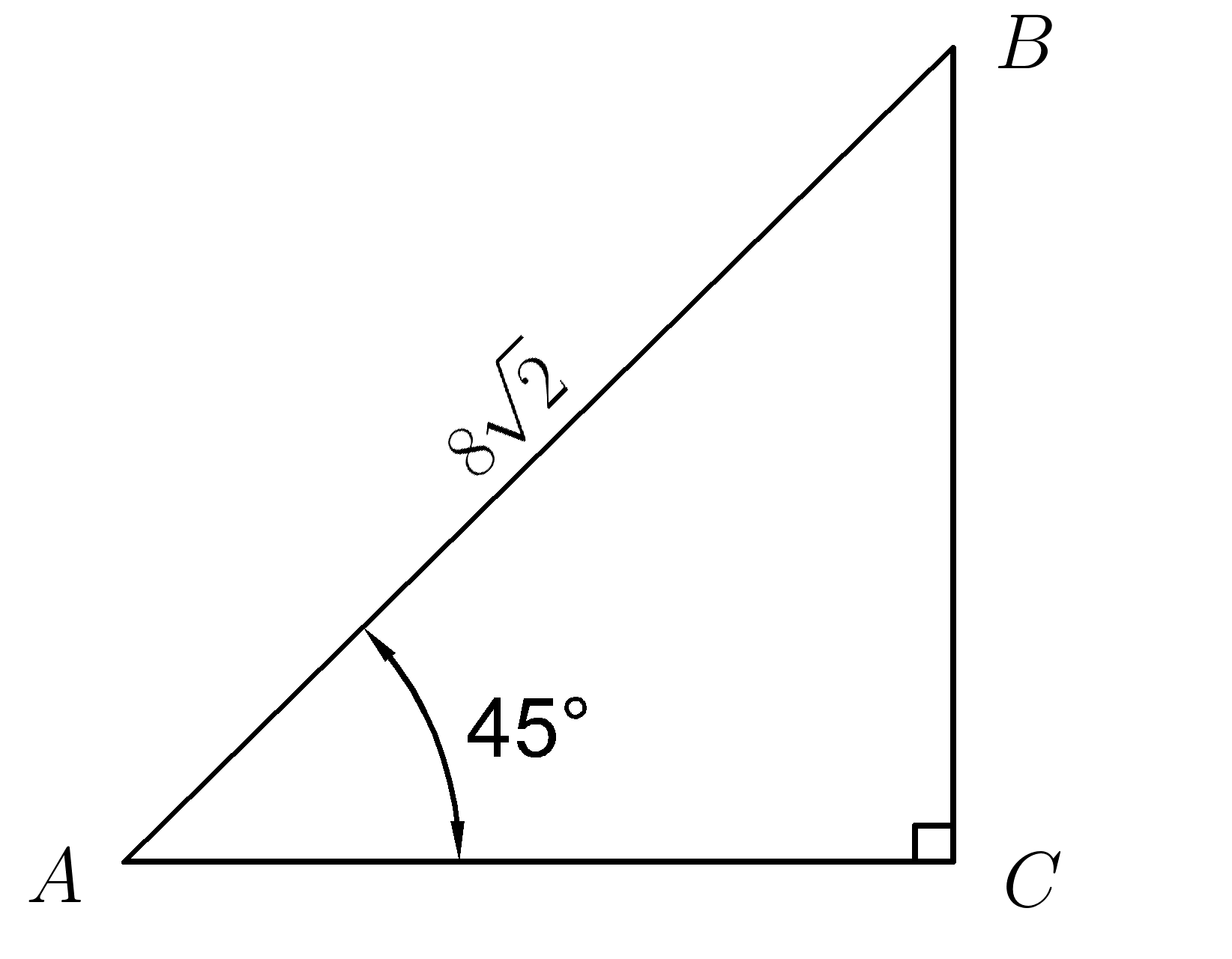
16. Гипотенуза $A B = 8 \sqrt{2}, ∡ B A C = 45^{0}, c o s 45^{0} = \frac{\sqrt{2}}{2}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 8$

$c o s A = \frac{\sqrt{2}}{2} c o s A = \frac{A C}{A B}$

$\frac{A C}{8 \sqrt{2}} = \frac{\sqrt{2}}{2}$

$A C = \frac{8 \sqrt{2} \cdot \sqrt{2}}{2}$

$A C = \frac{8 \cdot 2}{2} = 8$

Ответ: $A C = 8$

ПОЗЖЕ

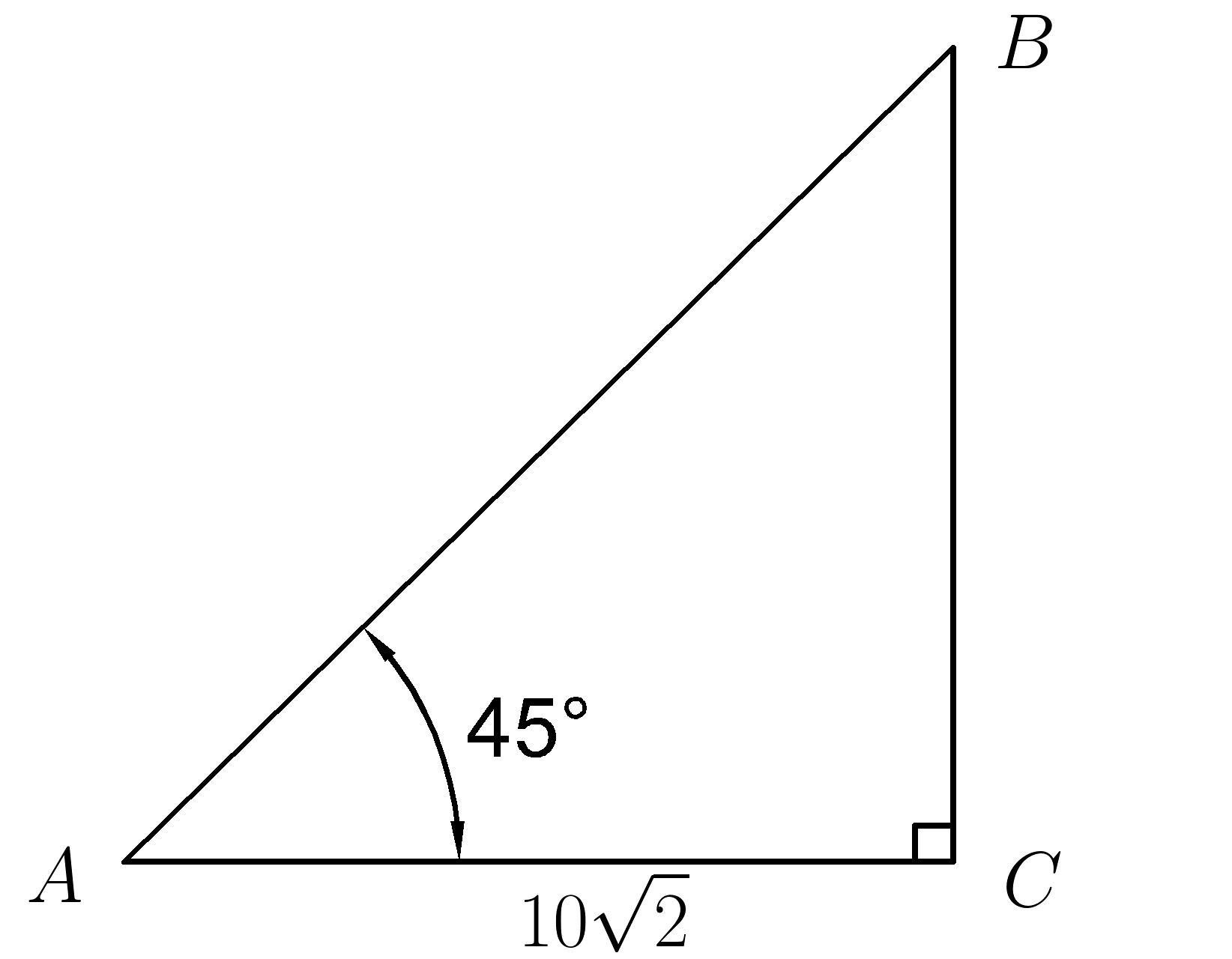
17. Катет $A C = 10 \sqrt{2}, ∡ B A C = 45^{0}, c o s 45^{0} = \frac{\sqrt{2}}{2}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 20$

$c o s A = \frac{\sqrt{2}}{2} c o s A = \frac{A C}{A B}$

$\frac{\sqrt{2}}{2} = \frac{10 \sqrt{2}}{A B}$

$A B \sqrt{2} = 2 \cdot 10 \sqrt{2}$

$A B = \frac{20 \sqrt{2}}{\sqrt{2}} = 20$

Ответ: $A B = 20$

ПОЗЖЕ

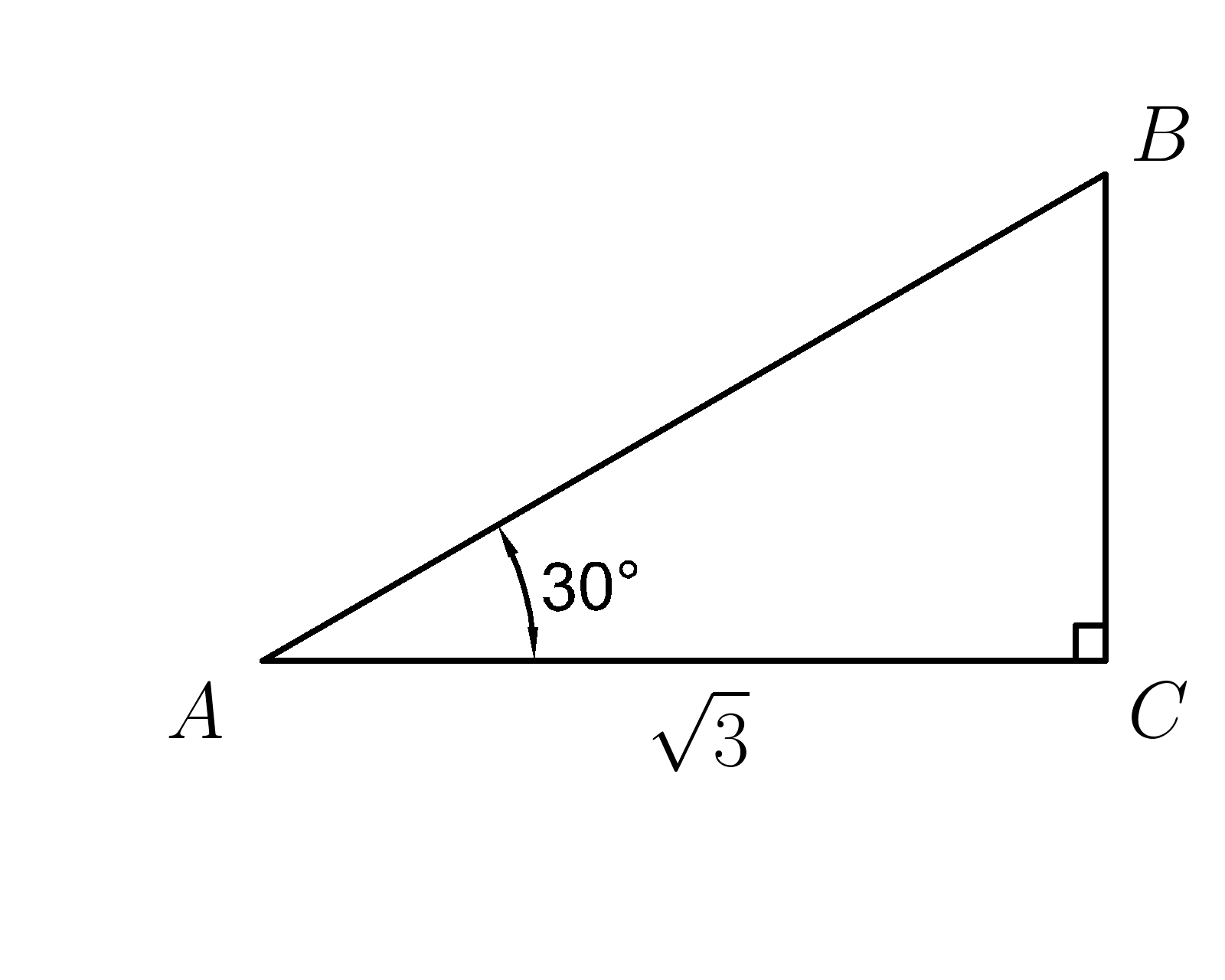
18. Катет $A C = \sqrt{3}, а ∡ B A C = 30^{0}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 2$

$c o s A = \frac{A C}{A B}$

$\frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{A B}$

$\sqrt{3} \cdot A B = 2 \sqrt{3}$

$A B = 2$

Ответ: $A B = 2$

ПОЗЖЕ

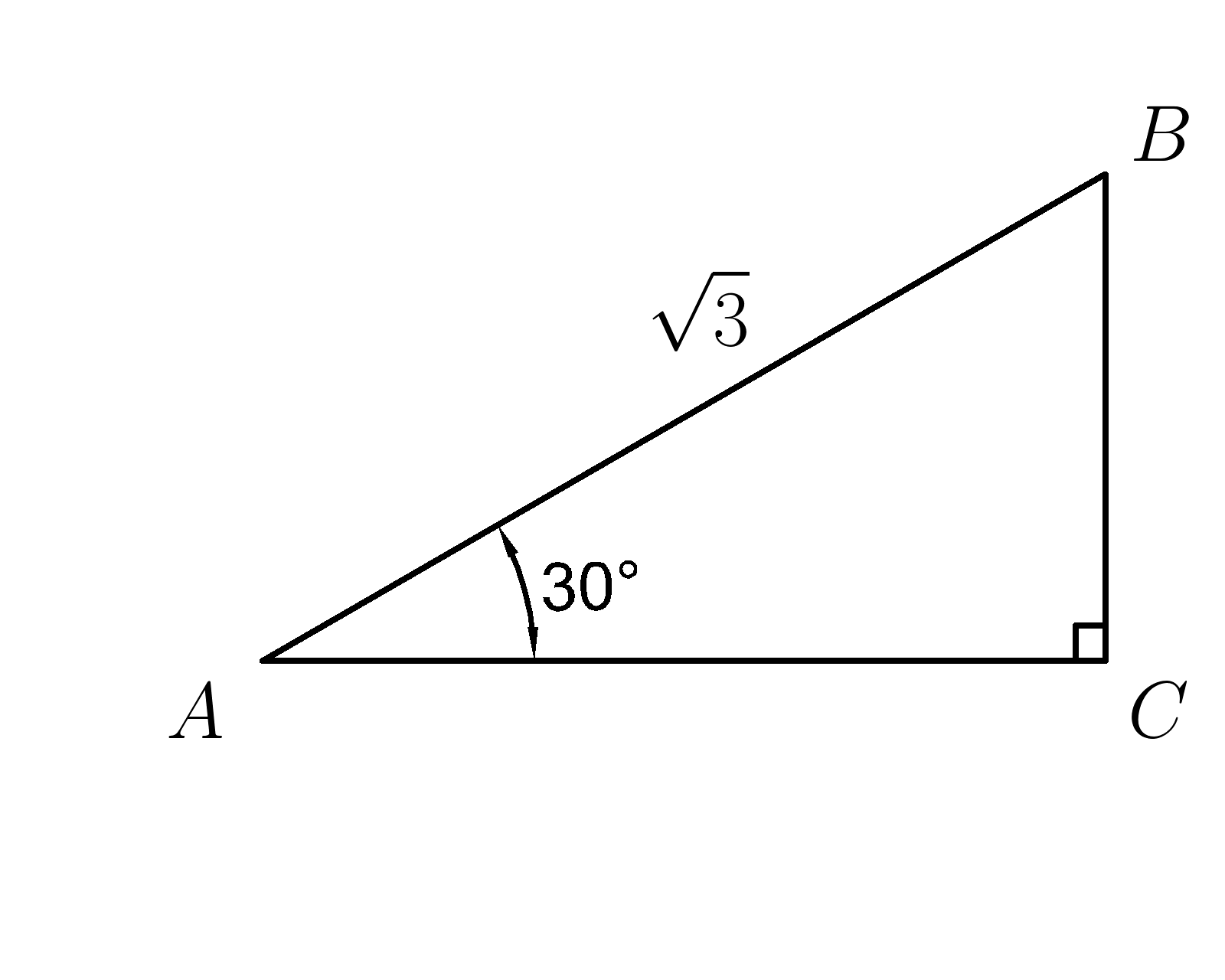
19. Гипотенуза $A B = \sqrt{3}, а ∡ B A C = 30^{0}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 1, 5$

$c o s A = \frac{A C}{A B}$

$\frac{\sqrt{3}}{2} = \frac{A C}{\sqrt{3}}$

$\frac{\sqrt{3}}{2} \cdot \sqrt{3} = \frac{A C}{\sqrt{3}} \cdot \sqrt{3}$

$\frac{3}{2} = A C$

$A C = \frac{3}{2} = 1, 5$

Ответ: $A C = 1, 5$

ПОЗЖЕ

20. Катет $B C = \sqrt{12} .$ Тангенс угла $A = \frac{1}{\sqrt{3}}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


$A C = 6$

$t g A = \frac{1}{\sqrt{3}} t g A = \frac{B C}{A C}$

$\frac{1}{\sqrt{3}} = \frac{\sqrt{12}}{A C}$

$A C = \sqrt{3} \cdot \sqrt{12}$

$A C = \sqrt{36} = 6$

Ответ: $A C = 6$

ПОЗЖЕ

21. Катет $B C = \sqrt{12} . t g A = \sqrt{3}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 2$

$t g A = \sqrt{3} t g A = \frac{B C}{A C}$

$\sqrt{3} = \frac{\sqrt{12}}{A C}$

$\sqrt{3} \cdot A C = \sqrt{12}$

$A C = \frac{\sqrt{12}}{\sqrt{3}}$

$A C = \sqrt{4} = 2$

Ответ: $A C = 2$

ПОЗЖЕ

22. Катет $A C = 10 \sqrt{2} . t g A = 1$ . Найти катет $B C$
Показать ответ Показать решение Видеорешение


Ответ: $B C = 10 \sqrt{2}$

Треугольник равнобедренный так как углы при гипотенузе равны $B C = A C = 10 \sqrt{2}$

$t g A = 1 t g A = \frac{B C}{A C}$

$1 = \frac{10 \sqrt{2}}{A C}$

$B C = 10 \sqrt{2}$

Ответ: $B C = 10 \sqrt{2}$

ПОЗЖЕ

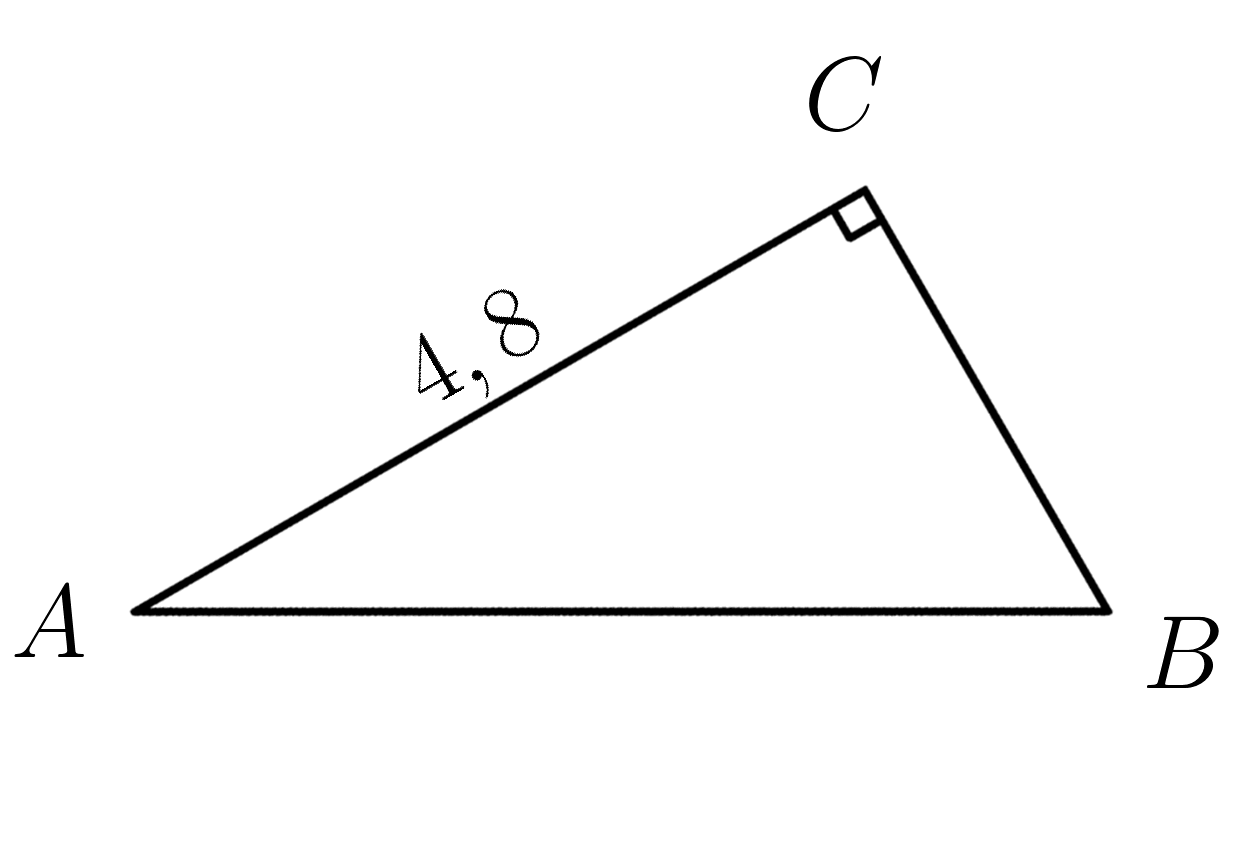
23. Катет $A C = 4, 8 . c o s A = \frac{24}{25}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 5$

$c o s A = \frac{24}{25} c o s A = \frac{A C}{A B}$

$\frac{24}{25} = \frac{4, 8}{A B}$

$24 \cdot A B = 25 \cdot 4, 8$

$24 \cdot A B = 120$

$A B = \frac{120}{24} = 5$

Ответ: $A B = 5$

ПОЗЖЕ

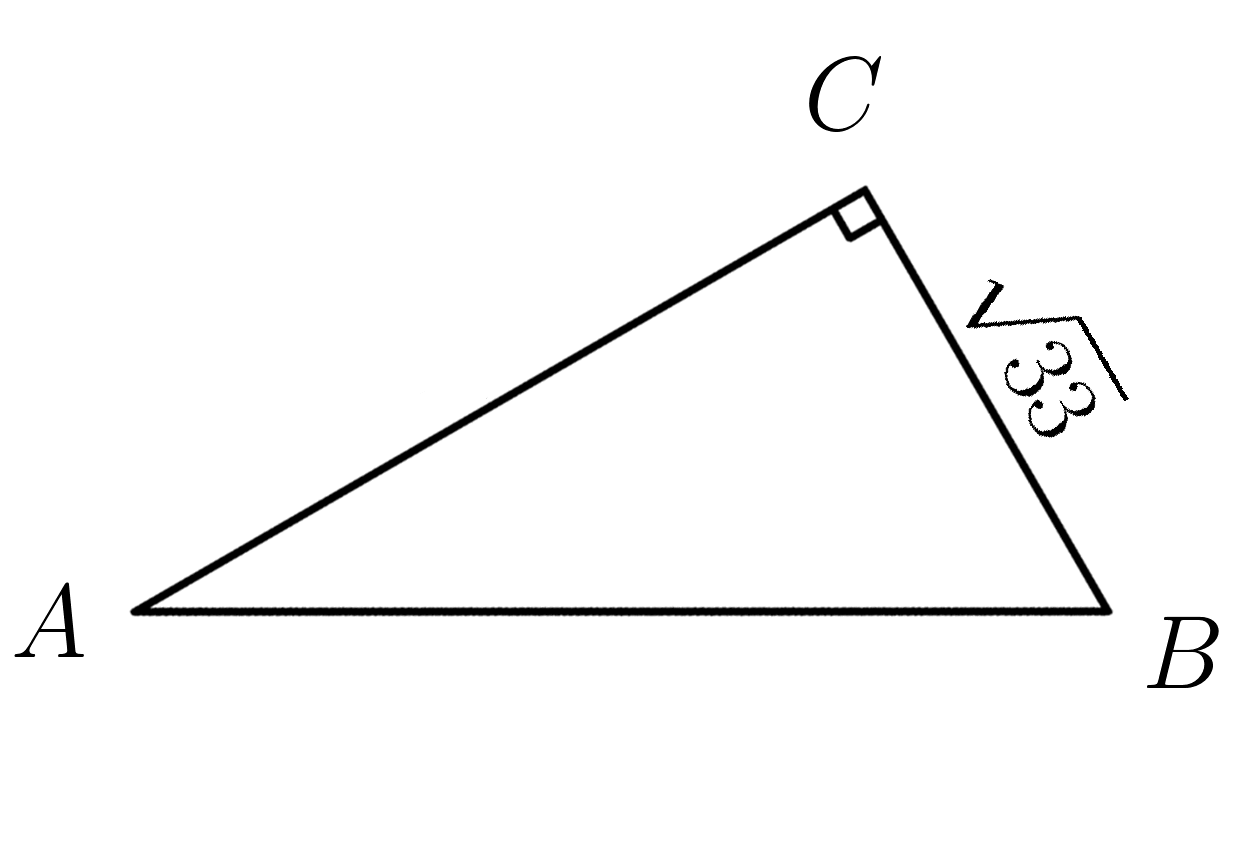
24. Катет $C B = \sqrt{33} . t g A = \frac{33}{4 \sqrt{33}}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 4$

$t g A = \frac{33}{4 \sqrt{33}} t g A = \frac{C B}{A C}$

$\frac{33}{4 \sqrt{33}} = \frac{\sqrt{33}}{A C}$

$33 \cdot A C = 4 \cdot \sqrt{33} \cdot \sqrt{33}$

$33 \cdot A C = 4 \cdot 33$

$A C = 4$

Ответ: $A C = 4$

ПОЗЖЕ

25. Катет $A C = \sqrt{3} . c o s A = \frac{2}{5 \sqrt{27}}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 22, 5$

$c o s A = \frac{2}{5 \sqrt{27}} c o s A = \frac{A C}{A B}$

$\frac{2}{5 \sqrt{27}} = \frac{\sqrt{3}}{A B}$

$2 \cdot A B = 5 \cdot \sqrt{27} \cdot \sqrt{3}$

$2 \cdot A B = 5 \cdot \sqrt{81}$

$2 \cdot A B = 5 \cdot 9$

$2 \cdot A B = 45$

$A B = \frac{45}{2} = 22, 5$

Ответ: $A B = 22, 5$

ПОЗЖЕ

26. Катет $C B = \sqrt{20} . c o s B = \frac{2}{3 \sqrt{5}}$ . Найти гипотенузу $A B$
Показать ответ Показать решение Видеорешение


Ответ: $A B = 15$

$c o s B = \frac{2}{3 \sqrt{5}} c o s B = \frac{C B}{A B}$

$\frac{2}{3 \sqrt{5}} = \frac{\sqrt{20}}{A B}$

$2 \cdot A B = 3 \cdot \sqrt{5} \cdot \sqrt{20}$

$2 \cdot A B = 3 \cdot \sqrt{100}$

$2 \cdot A B = 3 \cdot 10$

$2 \cdot A B = 30$

$A B = \frac{30}{2} = 15$

Ответ: $A B = 15$

ПОЗЖЕ

27. Катет $C B = \sqrt{2} . t g B = 4 \sqrt{32}$ . Найти катет $A C$
Показать ответ Показать решение Видеорешение


Ответ: $A C = 32$

$t g B = 4 \sqrt{32} t g B = \frac{A C}{C B}$

$4 \sqrt{32} = \frac{A C}{\sqrt{2}}$

$4 \sqrt{32} \cdot \sqrt{2} = A C$

$A C = 4 \sqrt{64}$

$A C = 4 \cdot 8 = 32$

Ответ: $A C = 32$

ПОЗЖЕ