Репетитор
по физике

916 478 1032




Репетитор
по алгебре

916 478 1032


Центральные и вписанные углы .


Центральные и вписанные углы

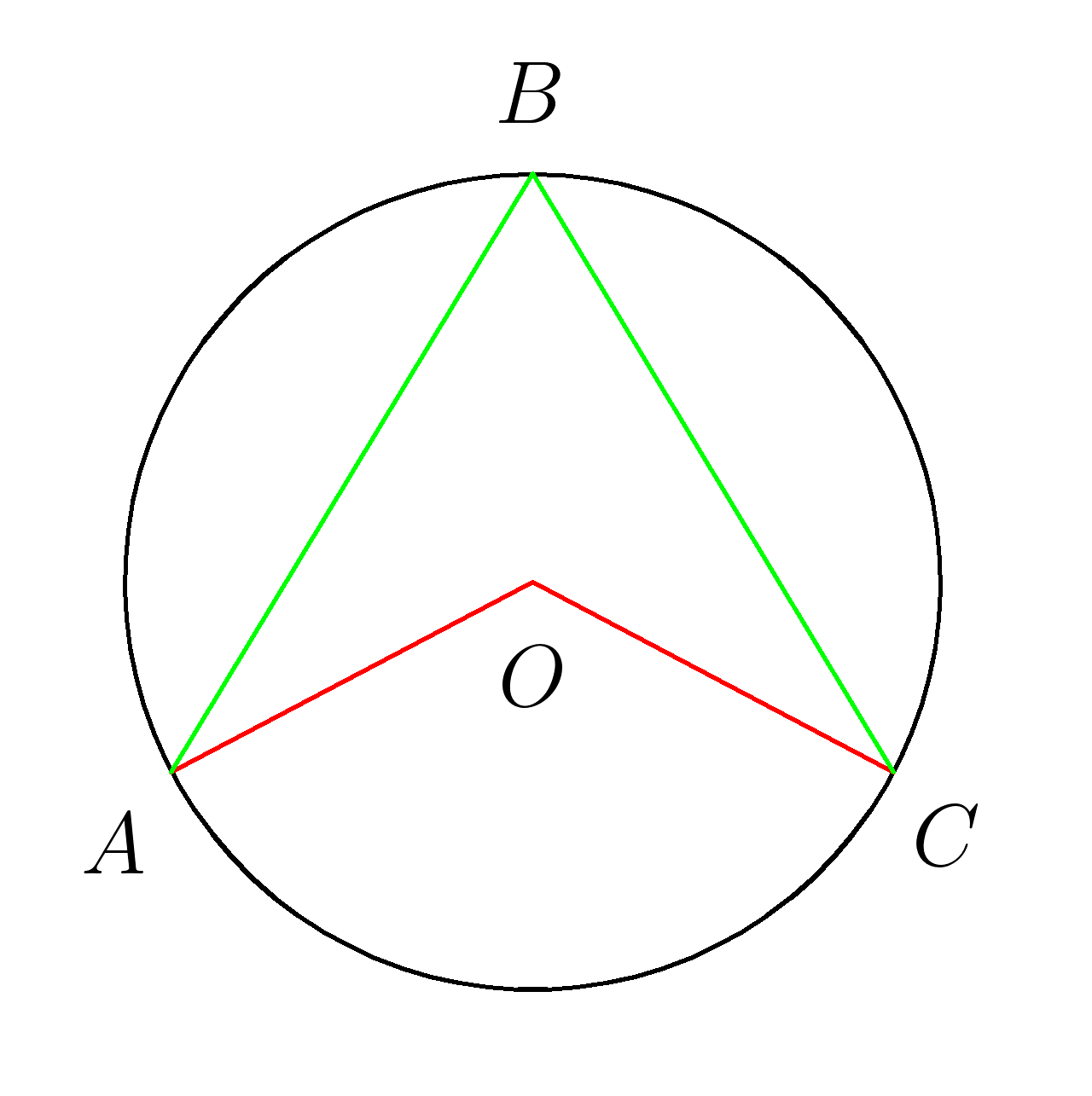
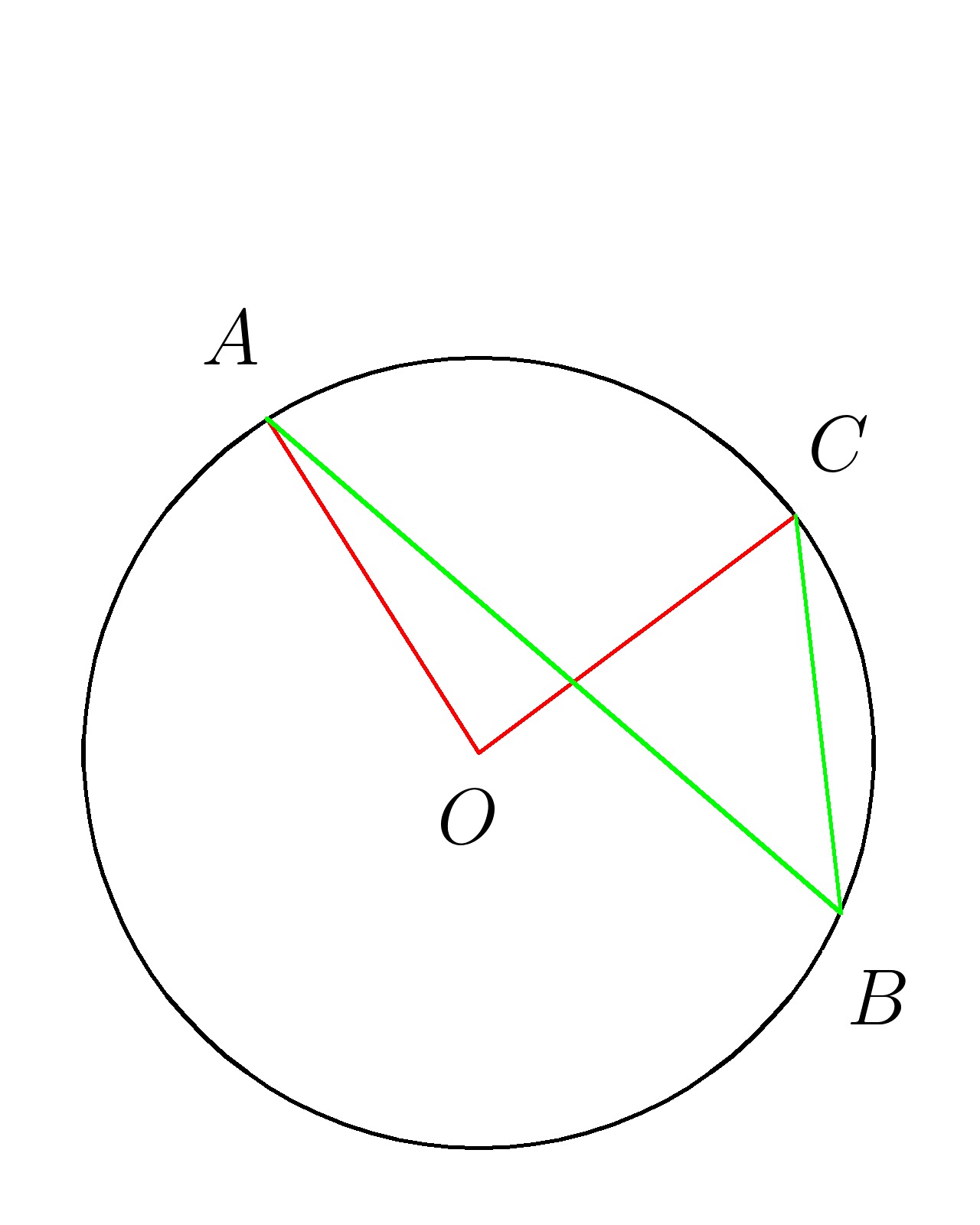
угол ABC вписанный

угол AOC центральный

оба угла опираются на дугу \(AC \)

Если вписанный и центральный углы опираются на одну и ту же дугу,то центральный угол в два раза больше вписанного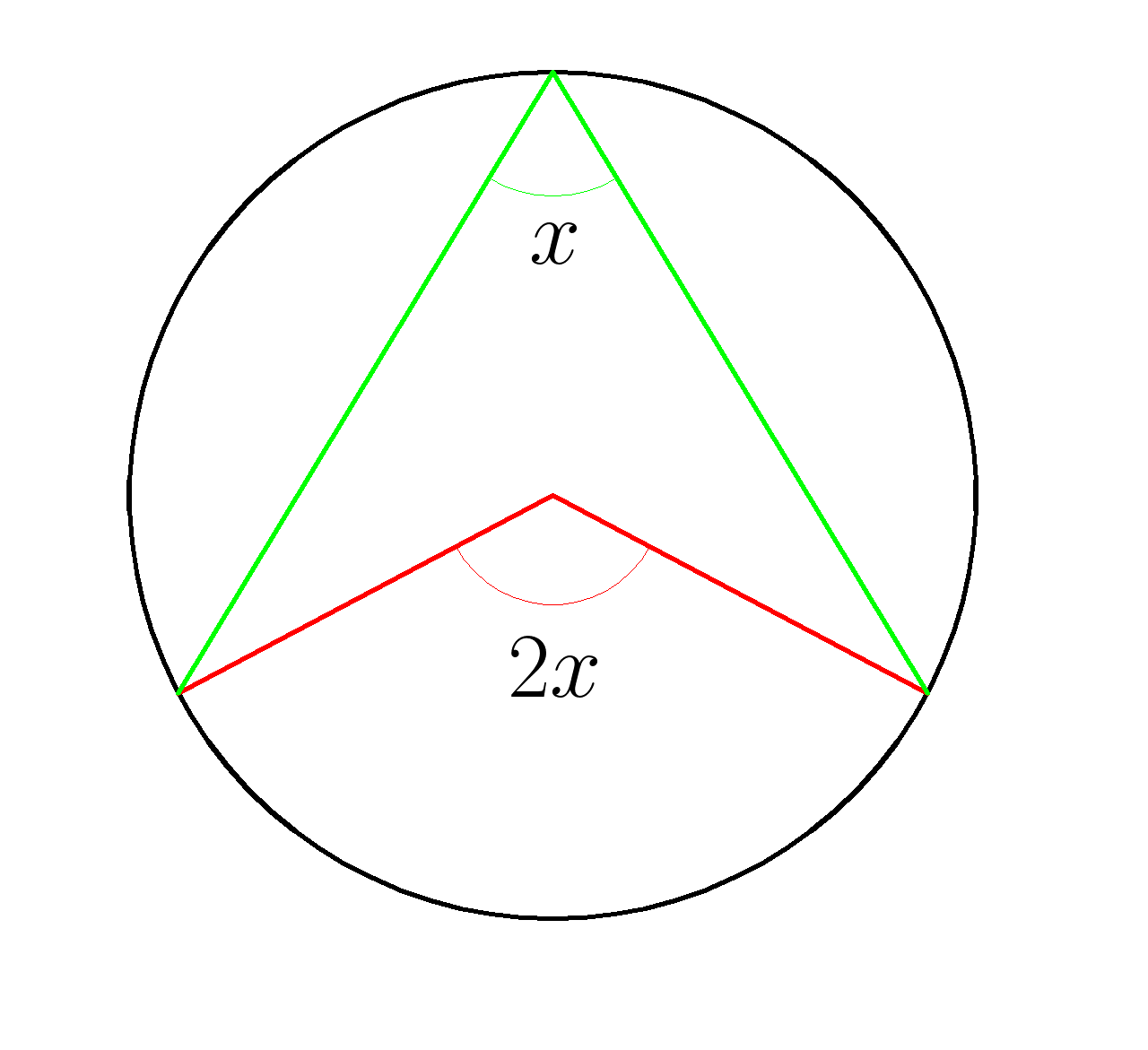
Центральные и вписанные углы



Вписанные и центральные углы

1.  \( \angle ABC=62^0 \) Найти угол \(AOC \)


  

Ответ: \(\angle AOC=124^0 \)

\( \angle AOC = 2 \cdot \angle ABC = 2 \cdot 62^0 = 124^0 \)

ПОЗЖЕ


Вписанные и центральные углы

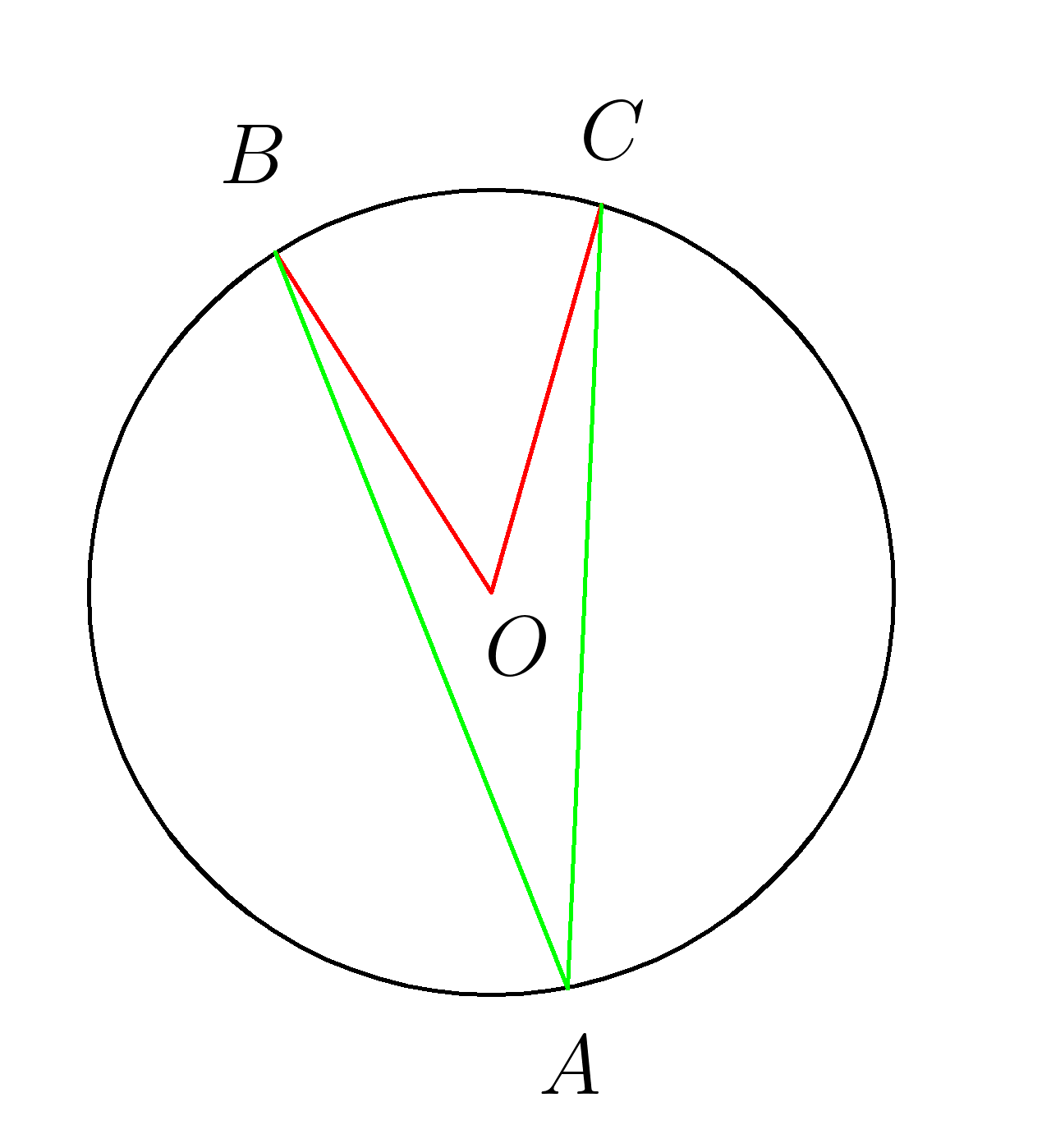
2.  \( \angle BAC=15^0 \). Найти \( \angle BOC \)


  

Ответ: \( \angle BOC = 30^0 \)

\( \angle BOC = 2 \cdot \angle BAC = 2 \cdot 15^0 = 30^0 \)

Ответ: \( \angle BOC = 30^0 \)


ПОЗЖЕ



Вписанные и центральные углы

3.  \( \angle AOC =110^0 \) Найти угол \(ABC \)


  

Ответ: \(\angle ABC=55^0 \)

\( \angle ABC = \dfrac { \angle AOC }{2} = \dfrac { 110^0 }{2} = 55^0 \)

ПОЗЖЕ



Вписанные и центральные углы

4.  \( \angle BOC =44^0 \) Найти угол \(BAC \)


  

Ответ: \(\angle BAC=22^0 \)

\( \angle BAC = \dfrac { \angle BOC }{2} = \dfrac { 44^0 }{2} = 22^0 \)

ПОЗЖЕ



Вписанные и центральные углы

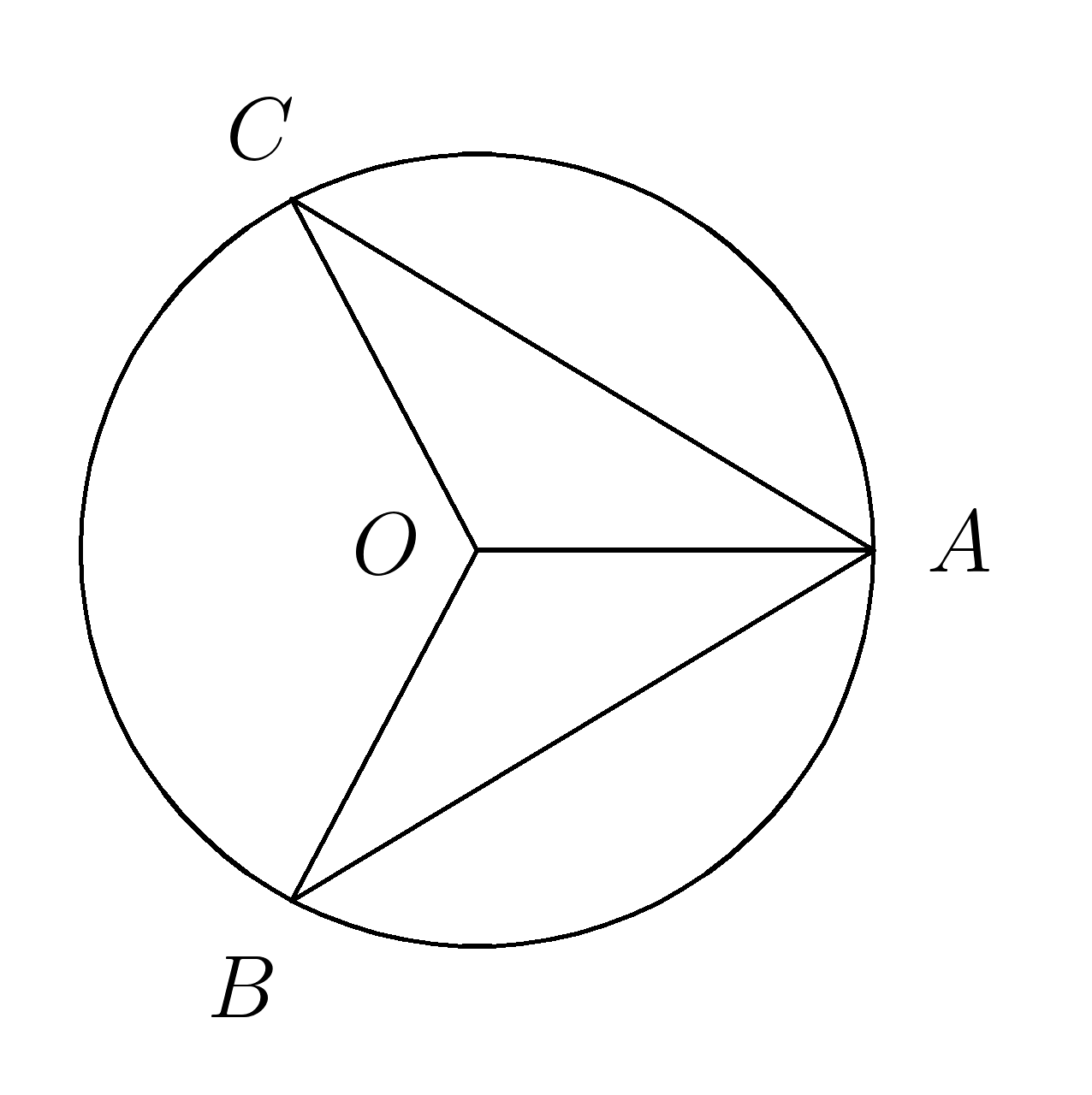
5.  \( \angle BOC =144^0, \;\; AO \) является биссектрисой угла \( CAB. \) Найти угол \(CAO \)


  

Ответ: \(\angle CAO=36^0 \)

\( \angle CAB = \dfrac { \angle BOC }{2} = \dfrac { 144^0 }{2} = 72^0 \)

\( \angle CAO = \dfrac { \angle CAB }{2} \) (Так как \( AO \) биссектриса )

\( \angle CAO = \dfrac { 72^0 }{2}=36^0 \)

Ответ: \(\angle CAO=36^0 \)


ПОЗЖЕ



Вписанные и центральные углы

6.  \( \angle BAO =34^0, \;\; AO \) является биссектрисой угла \( CAB. \) Найти угол \(COB \)


  

Ответ: \(\angle COB=136^0 \)

\( \angle CAB = 2 \cdot \angle BAO = 2 \cdot 34^0 = 68^0 \) (Так как \( AO \) биссектриса )

\( \angle COB = 2 \cdot \angle CAB =2 \cdot 68^0=136^0 \)

Ответ: \(\angle COB=136^0 \)


ПОЗЖЕ



Вписанные и центральные углы

7.  \( \angle OBA =34^0, \;\; AO \) является биссектрисой угла \( CAB. \) Найти угол \(COB \)


  

Ответ: \(\angle COB=136^0 \)

\(OB=OA\) так как это радиусы окружности,

значит \( \Delta BAO \) равнобедренный

в равнобедренном треугольнике углы при основании равны

\( \angle BAO = \angle OBA= 34^0 \)

\( \angle CAB = 2 \cdot \angle BAO = 2 \cdot 34^0 = 68^0 \) (Так как \( AO \) биссектриса )

\( \angle COB = 2 \cdot \angle CAB =2 \cdot 68^0=136^0 \)

Ответ: \(\angle COB=136^0 \)


ПОЗЖЕ



Вписанные и центральные углы

8.  \( \angle BOA =100^0, \;\; AO \) является биссектрисой угла \( CAB. \) Найти угол \(COB \)


  

Ответ: \(\angle COB=160^0 \)

\(OB=OA\) так как это радиусы окружности,

значит \( \Delta BAO \) равнобедренный

в равнобедренном треугольнике углы при основании равны

\( \angle BAO = \angle OBA=x\)

\( \angle BAO + \angle OBA+\angle BOA =180^0 \)

\(x+x+100=180 \)

\(2x=180-100 \)

\(x=40 \)

\( \angle BAO = \angle OBA=40^0\)

\( \angle CAB = 2 \cdot \angle BAO = 2 \cdot 40^0 = 80^0 \) (Так как \( AO \) биссектриса )

\( \angle COB = 2 \cdot \angle CAB =2 \cdot 80^0=160^0 \)

Ответ: \(\angle COB=160^0 \)


ПОЗЖЕ




Вписанные и центральные углы

9.  \( \angle ABC=62^0 \) Найти угол \(AOC \)


  

Ответ: \(\angle AOC=124^0 \)

\( \angle AOC \) центральный

\( \angle ABC \) вписанный

\( \angle AOC = 2 \cdot \angle ABC = 2 \cdot 62^0 = 124^0 \)

Ответ: \(\angle AOC=124^0 \)


ПОЗЖЕ