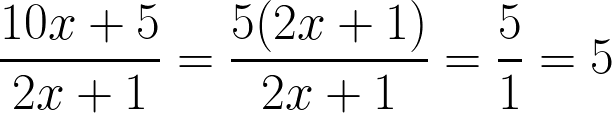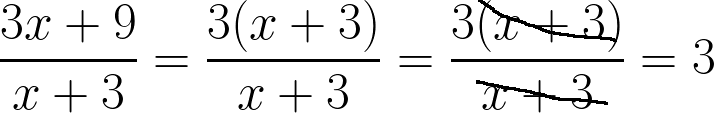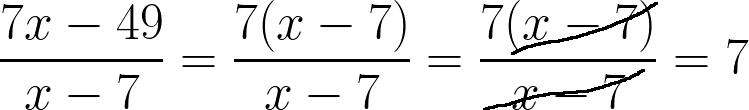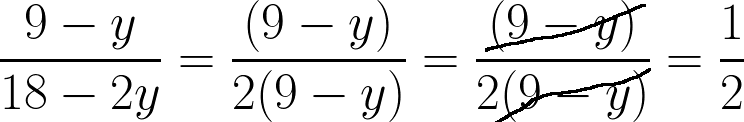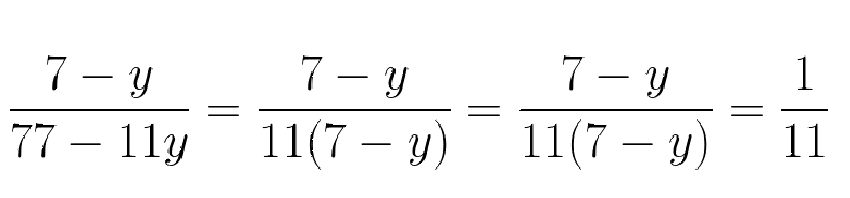Преобразование дробных выражений
1. Сократить дробь:
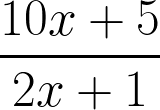
Показать решение
2. Сократить дробь:
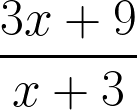
Показать ответ
3. Сократить дробь:
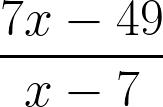
Показать ответ
4. Сократить дробь:
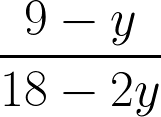
Показать ответ
5. Сократить дробь:
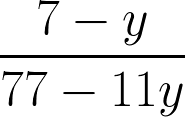
Показать ответ
6. \( \dfrac{x^2 -xy}{y}\cdot \dfrac{y^2}{x} \)
Показать ответ Показать решение Видеорешение
7. \( \dfrac{3a}{b^2} \cdot \dfrac{ab+b^2}{9} \)
Показать ответ Показать решение Видеорешение
8. \( \dfrac{n-m}{mn} \cdot \dfrac{2mn}{mn-m^2} \)
Показать ответ
Показать решение
Видеорешение
9. \( \dfrac{4ab}{cx+dx} \cdot \dfrac{ax+bx}{2ab} \)
Показать ответ
Показать решение
Видеорешение