Движение тела по наклонной плоскости
Репетитор по физике
8 916 478 10 32
Пройти тест на эту тему
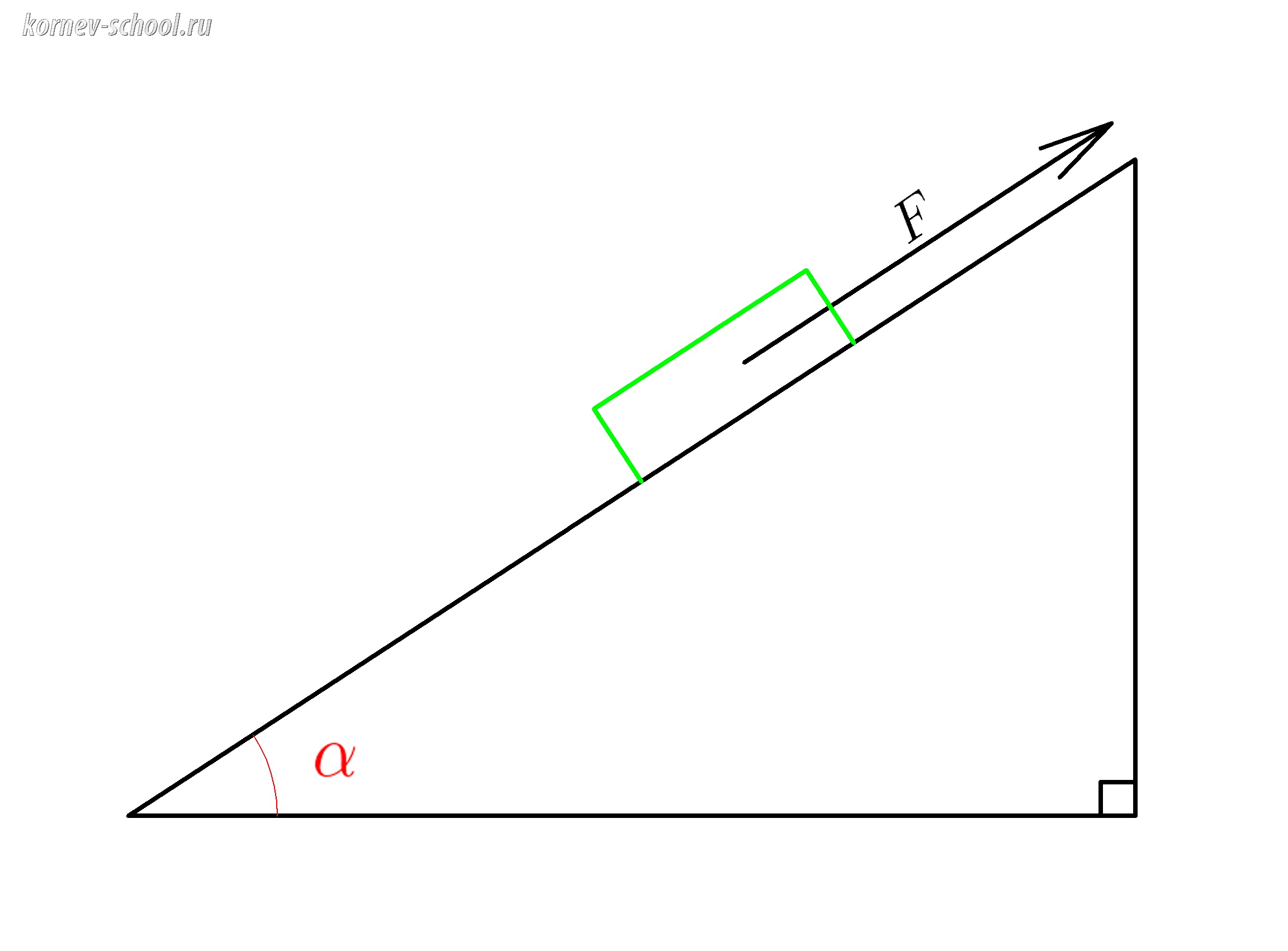
Тело на наклонной плоскости с углом наклона \( \alpha \)
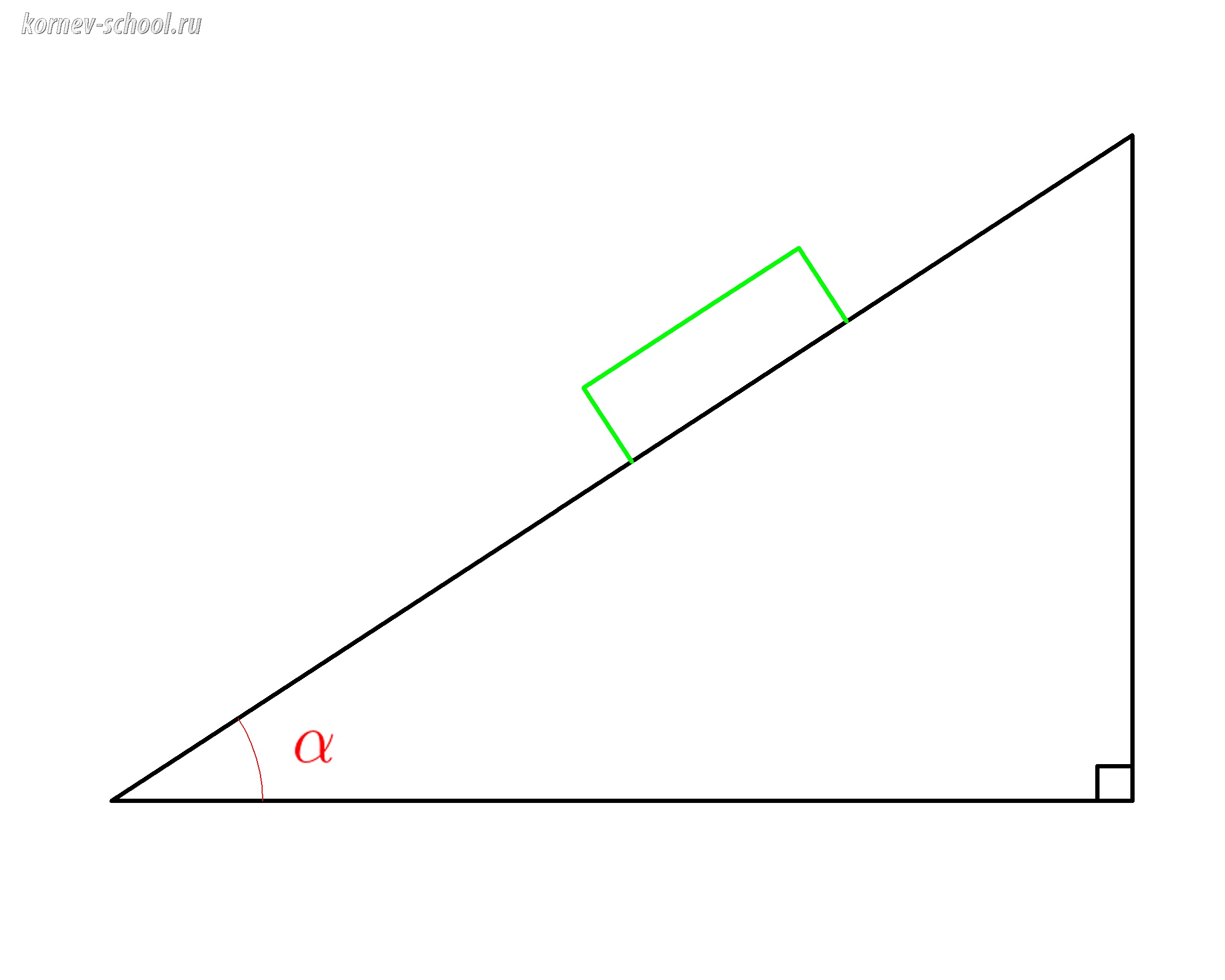
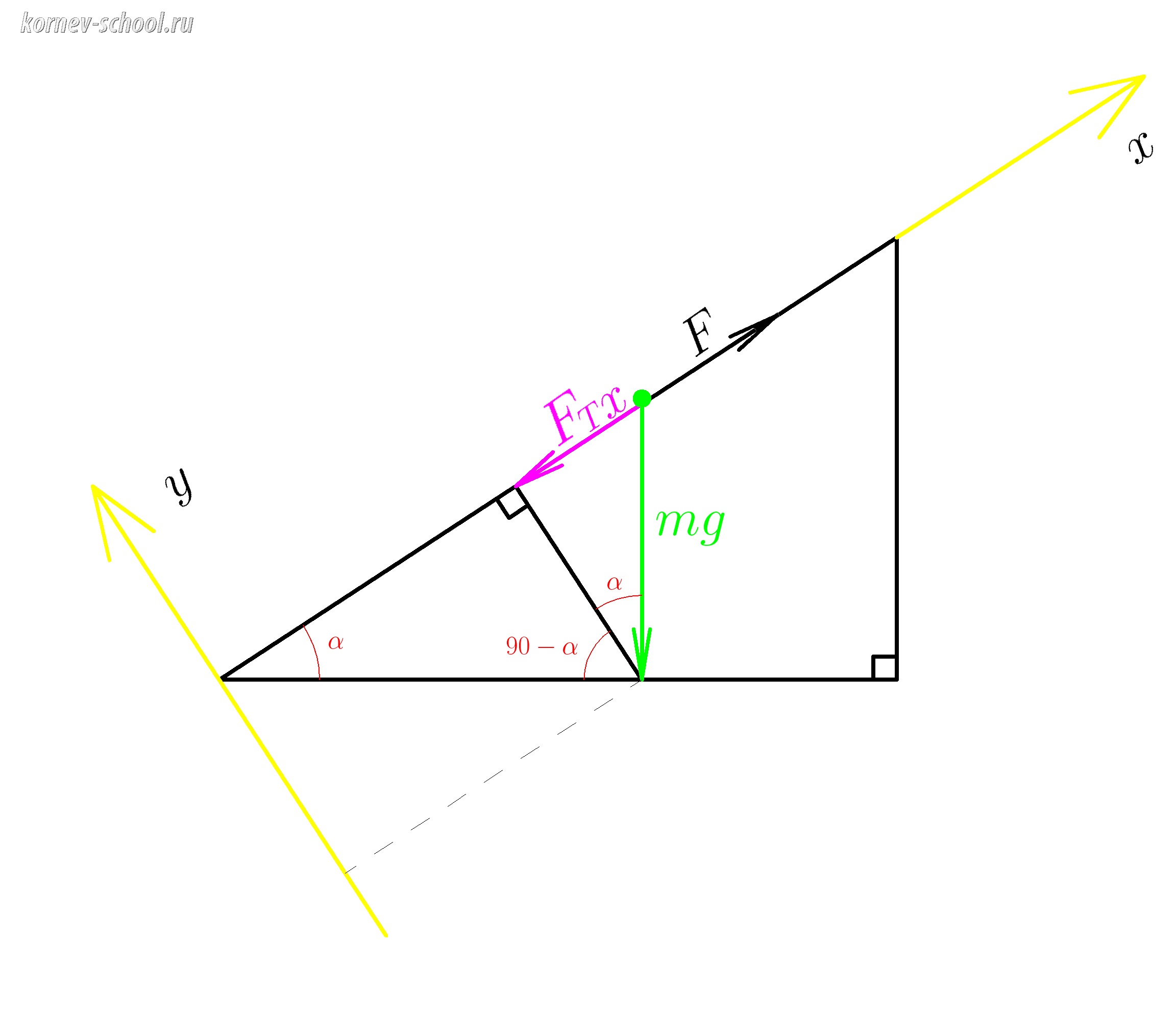
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
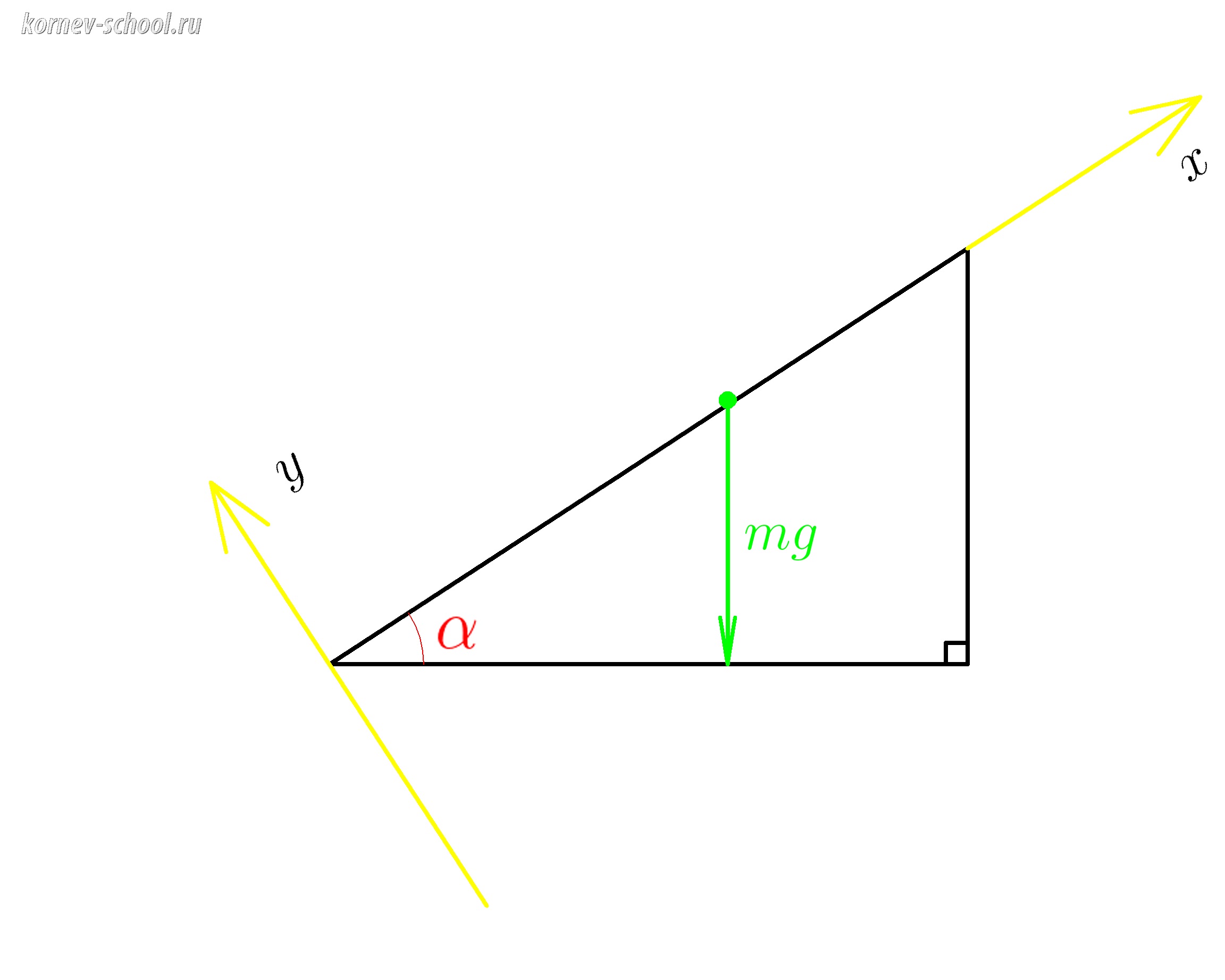
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей
Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
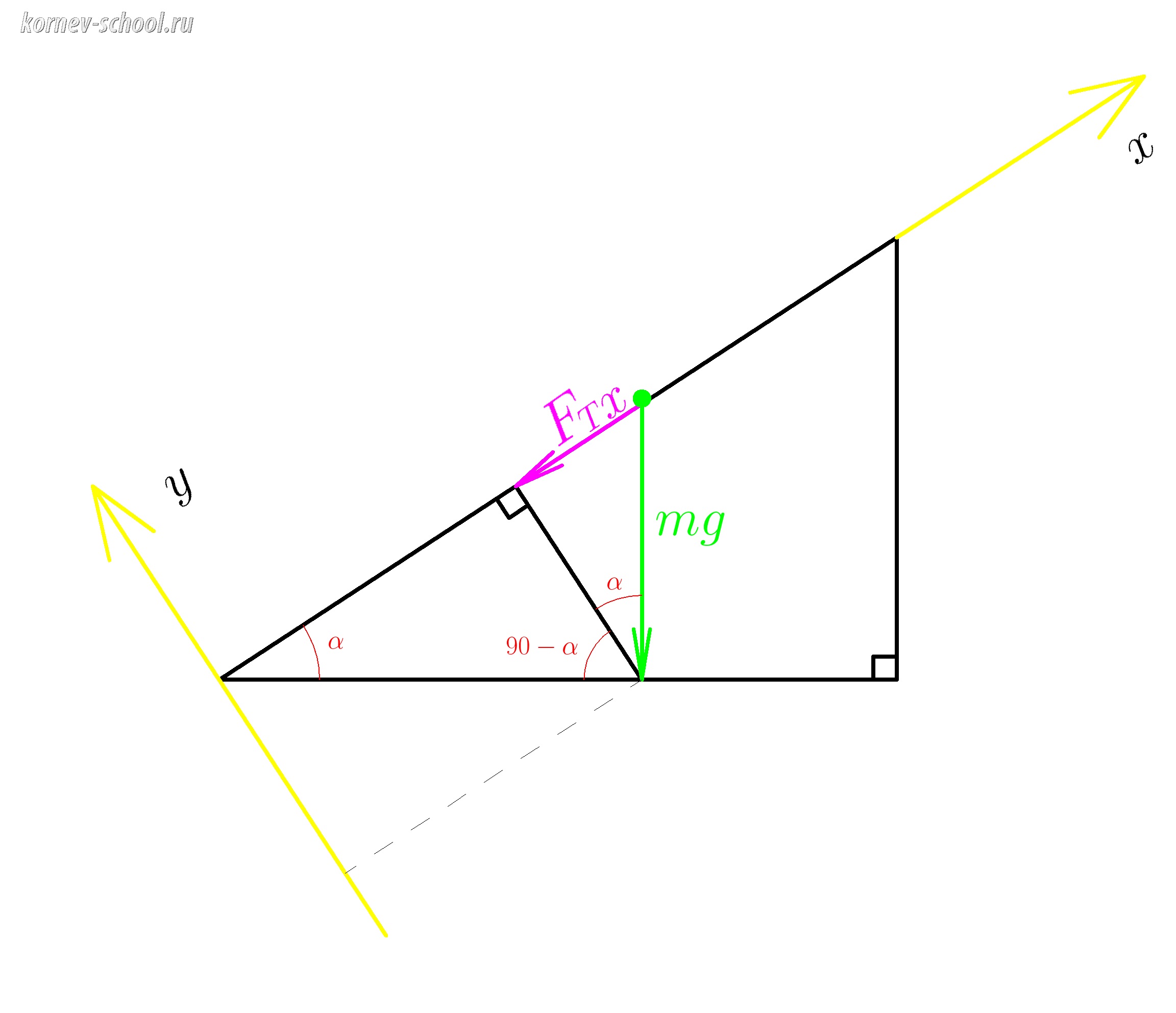
Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом
\(F_{тx} \; \)
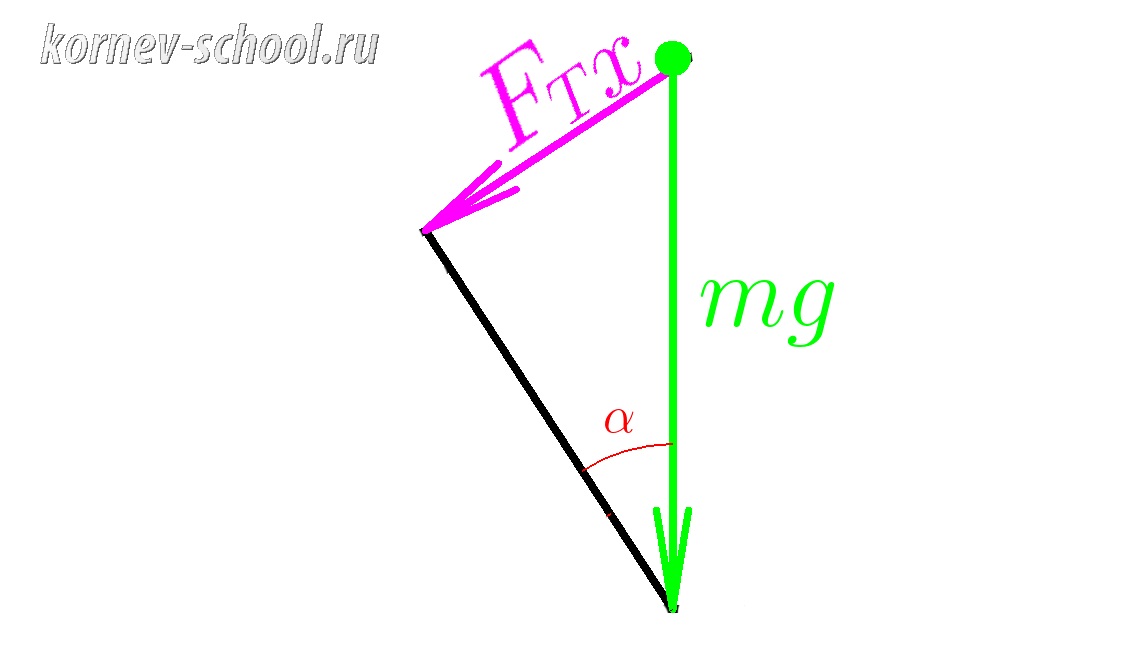
\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
Задача 1.
К телу массой \(m=1 кг \), покоящемуся на гладкой наклонной плоскости с углом наклона \( \alpha=30^0 \), приложена сила \(F\),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы \(F\)
Показать ответ
Показать решение
Видеорешение
Дано:
\( m=1 / кг \)
\( \alpha=30^0 \)
\(F-?\)
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) - Внешняя сила, которую нужно найти.
Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
По первому закону Ньютона:
\(F- F_{Тx}=0 \)
\(F- mg \cdot sin \; \alpha =0 \)
\(F= mg \cdot sin \; \alpha =1 кг \cdot 10 м/с^2 \cdot sin \;30^0=5Н \)
Ответ: \( F=5Н \)
Задача 2.
К телу массой \(m=2 кг \), покоящемуся на гладкой наклонной плоскости с углом наклона \( \alpha=30^0 \), приложена сила \(F\),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы \(F\)

Показать ответ
Показать решение
Видеорешение
Дано:
\( m=2 кг \)
\( \alpha=30^0 \)
\(F-?\)
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) - Внешняя сила, которую нужно найти.

Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
По первому закону Ньютона:
\(F- F_{Тx}=0 \)
\(F- mg \cdot sin \; \alpha =0 \)
\(F= mg \cdot sin \; \alpha =2 кг \cdot 10 м/с^2 \cdot sin \;30^0=10Н \)
Ответ: \( F=10Н \)
Задача 3.
К телу массой \(m=\sqrt{2} кг \), покоящемуся на гладкой наклонной плоскости с углом наклона \( \alpha=45^0 \), приложена сила \(F\),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы \(F\)

Показать ответ
Показать решение
Видеорешение
Дано:
\( m=\sqrt{2} кг \)
\( \alpha=45^0 \)
\(F-?\)
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) - Внешняя сила, которую нужно найти.

Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
По первому закону Ньютона:
\(F- F_{Тx}=0 \)
\(F- mg \cdot sin \; \alpha =0 \)
\(F= mg \cdot sin \; \alpha =\sqrt{2} \cdot 10 \cdot sin \;45^0= \sqrt{2} \cdot 10 \cdot \dfrac{\sqrt{2}}{2}= 10 Н \)
Ответ: \( F=10Н \)
Задача 4.
К телу массой \(m=\sqrt{27} кг \), покоящемуся на гладкой наклонной плоскости с углом наклона \( \alpha=60^0 \), приложена сила \(F\),
направленная вдоль наклонной плоскости, поэтому тело не соскальзывает, а покоится.
Найти значение этой силы \(F\)

Показать ответ
Показать решение
Видеорешение
Дано:
\( m=\sqrt{27} кг \)
\( \alpha=60^0 \)
\(F-?\)
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x
\(F\) - Внешняя сила, которую нужно найти.

Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
По первому закону Ньютона:
\(F- F_{Тx}=0 \)
\(F- mg \cdot sin \; \alpha =0 \)
\(F= mg \cdot sin \; \alpha =\sqrt{27} \cdot 10 \cdot sin \;60^0= \sqrt{27} \cdot 10 \cdot \dfrac{\sqrt{3}}{2}= 5 \sqrt{81} =45 Н \)
Ответ: \( F=45Н \)
Пройти тест на эту тему
Задача 6.
С каким ускорением \(a \) движется тело по гладкой наклонной плоскости с углом наклона \( \alpha=45^0 \; ? \)
Ускорение свободного падения \( g=10м/с^2 \; \)
Ответ округлить до сотых

Показать ответ
Показать решение
Видеорешение
Ответ: \( a=7,07 м/с^2 \)
Дано:
\( \alpha=45^0 \)
\(a-?\)
Уменьшим размеры тела для того, чтобы его габариты не мешали разбираться построении векторов и их проекций.
Жирная зеленая точка это и есть наше тело.
Проведем из нее вектор силы тяжести \(mg\).
При решении задач на движение тела по наклонной плоскости мы направляем ось \( x \) вдоль гипотенузы,а ось \( y \)
перпендикулярно ей

Проведем перпендикуляр из конца вектора силы тяжести на ось \( x \)
\(F_{тx} \; \) это проекция силы тяжести на ось x

Сфокусируем все свое внимание на прямоугольный треугольничек с зелененькой гипотенузой
\(mg \)
и фиолетовым катетом \(F_{тx} \; \)

\(sin \; \alpha=\dfrac{F_{Тx}}{mg} \)
\( F_{Тx}= mg \cdot sin \; \alpha \;\;\;\;\; \) это мы нашли проекцию силы тяжести на ось \(x\)
По второму закону Ньютона:
\( F_{Тx}=ma \)
\( mg \cdot sin \; \alpha = ma \)
\( g \cdot sin \; \alpha = a \)
\(a= g \cdot sin \; \alpha =10\cdot sin 45^0=10\cdot \dfrac{\sqrt{2}}{2}=7,07106781187 \approx 7,07 м/с^2 \)
Ответ: \(a=7,07 м/с^2 \)
Пройти тест на эту тему









