Закон сохранения энергии .
Сумма кинетической и потенциальной энергии не меняется.
(Если нет внешних сил) (внешняя сила -любая сила кроме силы тяжести)
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Пройти тест на эту тему (5 задач)
1. Футбольный мяч падает без начальной скорости с высоты \(h=20 м \).
Найти его скорость перед столкновением с землей.
Показать ответ
Показать решение
Видеорешение
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Начальная скорость \(v_1=0 \) равна нулю, а значит и кинетическая энергия \(E_{к1}=0 \)
конечная высота тела \(h_2\) равна нулю, это значит что потенциальная энергия \(E_{п2}=0 \)
Преобразуем уравнение закона сохранения энергии под условие этой задачи:
\(0+ mgh_1= \dfrac{ mv_2^2}{2}+0 \)
\( mgh_1= \dfrac{ mv_2^2}{2} \)
избавимся от индексов для простоты:
\( mgh= \dfrac{ mv^2}{2} \)
Дано:
\( h_1=20 м \)
\( g=10м/с^2 \; \)
\(v-? \)
Запишем закон сохранения энергии :
\(0+ mgh= \dfrac{ mv^2}{2}+0 \)
\( mgh= \dfrac{ mv^2}{2} \; \; \; \; \; \; делим \; обе \; части \; уравнения \; на \; массу: \)
\( gh= \dfrac{ v^2}{2} \)
\(2gh=v^2 \)
\( v=\sqrt{2gh} \)
\( v=\sqrt{2\cdot 10м/с^2 \cdot 20м }=20 м/с \)
Ответ: \( v= 20 м/с \)
2. Камень падает без начальной скорости с высоты \(h=11,25 м \).
Найти его скорость перед столкновением с землей.
Показать ответ
Показать решение
Видеорешение
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Начальная скорость \(v_1=0 \) равна нулю, а значит и кинетическая энергия \(E_{к1}=0 \)
конечная высота тела \(h_2\) равна нулю, это значит что потенциальная энергия \(E_{п2}=0 \)
Преобразуем уравнение закона сохранения энергии под условие этой задачи:
\(0+ mgh_1= \dfrac{ mv_2^2}{2}+0 \)
\( mgh_1= \dfrac{ mv_2^2}{2} \)
избавимся от индексов для простоты:
\( mgh= \dfrac{ mv^2}{2} \)
Дано:
\( h_1=20 м \)
\( g=10м/с^2 \; \)
\(v-? \)
Запишем закон сохранения энергии :
\(0+ mgh= \dfrac{ mv^2}{2}+0 \)
\( mgh= \dfrac{ mv^2}{2} \; \; \; \; \; \; делим \; обе \; части \; уравнения \; на \; массу: \)
\( gh= \dfrac{ v^2}{2} \)
\(2gh=v^2 \)
\( v=\sqrt{2gh} \)
\( v=\sqrt{2\cdot 10м/с^2 \cdot 11,25м }=15 м/с \)
Ответ: \( v= 15 м/с \)
3. Теннисный мячик падает без начальной скорости с высоты \(h=28,8 м \).
Найти его скорость перед столкновением с землей.
Показать ответ
Показать решение
Видеорешение
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Начальная скорость \(v_1=0 \) равна нулю, а значит и кинетическая энергия \(E_{к1}=0 \)
конечная высота тела \(h_2\) равна нулю, это значит что потенциальная энергия \(E_{п2}=0 \)
Преобразуем уравнение закона сохранения энергии под условие этой задачи:
\(0+ mgh_1= \dfrac{ mv_2^2}{2}+0 \)
\( mgh_1= \dfrac{ mv_2^2}{2} \)
избавимся от индексов для простоты:
\( mgh= \dfrac{ mv^2}{2} \)
Дано:
\( h_1=28,8 м \)
\( g=10м/с^2 \; \)
\(v-? \)
Запишем закон сохранения энергии :
\(0+ mgh= \dfrac{ mv^2}{2}+0 \)
\( mgh= \dfrac{ mv^2}{2} \; \; \; \; \; \; делим \; обе \; части \; уравнения \; на \; массу: \)
\( gh= \dfrac{ v^2}{2} \)
\(2gh=v^2 \)
\( v=\sqrt{2gh} \)
\( v=\sqrt{2\cdot 10м/с^2 \cdot 28,8м }=24 м/с \)
Ответ: \( v= 24 м/с \)
4. Произведен выстрел из зенитной пушки.Снаряд летит вертикально вверх со скоростью
\(v=300 м/с \). Какой максимальной высоты достигнет снаряд?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Начальная высота \(h_1=0 \) равна нулю, а значит и потенциальная энергия \(E_{п1}=0 \)
скорость тела в верхней точке \(v_2\) равна нулю, это значит что кинетическая энергия \(E_{к2}=0 \)
Преобразуем уравнение закона сохранения энергии под условие этой задачи:
\(\dfrac{ mv_1^2}{2}+0 =mgh_2 +0 \)
\( \dfrac{ mv_2^2}{2}=mgh_1 \)
избавимся от индексов для простоты:
\( \dfrac{ mv^2}{2}= mgh\)
Дано:
\( v=300 м/с \)
\( g=10м/с^2 \; \)
\(h-? \)
Запишем закон сохранения энергии :
\( \dfrac{ mv^2}{2}+0=0+ mgh\)
\( \dfrac{ mv^2}{2}=mgh \; \; \; \; \; \; делим \; обе \; части \; уравнения \; на \; массу: \)
\( \dfrac{ v^2}{2}=gh \)
\( \dfrac{ v^2}{2g}=h \)
\( h= \dfrac{ v^2}{2g} \)
\( h= \dfrac{ (300м/с)^2}{2\cdot 10м/с^2}=4500м \)
Ответ: \( h= 4500м \)
5. На какой высоте находилась воздушная цель, если для достижения этой высоты
скорость снаряда,запущенного с поверхности Земли, должна быть не менее 400 м/с ?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= \dfrac{ mv_2^2}{2}+ mgh_2 \)
Начальная высота \(h_1=0 \) равна нулю, а значит и потенциальная энергия \(E_{п1}=0 \)
скорость тела в верхней точке \(v_2\) равна нулю, это значит что кинетическая энергия \(E_{к2}=0 \)
Преобразуем уравнение закона сохранения энергии под условие этой задачи:
\(\dfrac{ mv_1^2}{2}+0 =mgh_2 +0 \)
\( \dfrac{ mv_2^2}{2}=mgh_1 \)
избавимся от индексов для простоты:
\( \dfrac{ mv^2}{2}= mgh\)
Дано:
\( v=400 м/с \)
\( g=10м/с^2 \; \)
\(h-? \)
Запишем закон сохранения энергии :
\( \dfrac{ mv^2}{2}+0=0+ mgh\)
\( \dfrac{ mv^2}{2}=mgh \; \; \; \; \; \; делим \; обе \; части \; уравнения \; на \; массу: \)
\( \dfrac{ v^2}{2}=gh \)
\( \dfrac{ v^2}{2g}=h \)
\( h= \dfrac{ v^2}{2g} \)
\( h= \dfrac{ (400м/с)^2}{2\cdot 10м/с^2}=8000м \)
Ответ: \( h= 8000м \)
Пройти тест на эту тему (5 задач)
Задача 6
Снежок брошен вертикально вверх со скоростью \(v_1=10м/с .\)
На какой высоте \(h\) кинетическая энергия снежка равна его потенциальной энергии?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v_1=10 м/с \)
\( g=10м/с^2 \; \)
\( E_{к2}=E_{п2} \)
\(h-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= E_{к2}+E_{п2} \)
Начальная высота \(h_1=0 \) равна нулю, а значит и потенциальная энергия \(E_{п1}=0 \)
\( \dfrac{ mv_1^2}{2}+ 0= E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}= E_{к2}+E_{п2} \)
По условию задачи \( E_{к2}=E_{п2} \)
поэтому вместо \( E_{к2} \) напишем \(E_{п2} \)
\( \dfrac{ mv_1^2}{2}= E_{п2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}= 2E_{п2} \)
\( \dfrac{ mv_1^2}{2}= 2mgh \)
\( \dfrac{ v_1^2}{2}= 2gh \)
\(h= \dfrac{ v_1^2}{4g} \)
\(h= \dfrac{ (10м/с)^2}{4 \cdot 10 м/с^2}=2,5 м \)
Ответ: \( h= 2,5 м \)
Задача 7
Камень брошен вертикально вверх со скоростью \(v_1=9м/с .\)
На какой высоте \(h\) кинетическая энергия камня равна половине его потенциальной энергии?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v_1=9 м/с \)
\( g=10м/с^2 \; \)
\( E_{к2}=0,5E_{п2} \)
\(h-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh_1= E_{к2}+E_{п2} \)
Начальная высота \(h_1=0 \) равна нулю, а значит и потенциальная энергия \(E_{п1}=0 \)
\( \dfrac{ mv_1^2}{2}+ 0= E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}= E_{к2}+E_{п2} \)
По условию задачи \( E_{к2}=0,5E_{п2} \)
поэтому вместо \( E_{к2} \) напишем \(0,5E_{п2} \)
\( \dfrac{ mv_1^2}{2}= 0,5E_{п2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}= 1,5E_{п2} \)
\( \dfrac{ mv_1^2}{2}= 1,5mgh \)
\( mv_1^2= 3mgh \)
\( v_1^2= 3gh \)
\(h= \dfrac{ v_1^2}{3g} \)
\(h= \dfrac{ (9м/с)^2}{3 \cdot 10 м/с^2}=2,7 м \)
Ответ: \( h= 2,7 м \)
Задача 10
Мальчик подъезжает на самокате к спуску, скорость мальчика в начале спуска \( v_1=2 м/с. \)
Высота спуска \(h=2,25 м .\)
Найти скорость мальчика в конце спуска.
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v_1=2 м/с \)
\( g=10м/с^2 \; \)
\( h=2,25 м \)
\(v_2-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+ mgh= E_{к2}+0 \)
\( \dfrac{ mv_1^2}{2}+ mgh=\dfrac{ mv_2^2}{2} \)
\( mv_1^2+ 2mgh= mv_2^2 \)
\( v_1^2+ 2gh= v_2^2 \)
\( v_2^2= v_1^2+ 2gh \)
\( v_2=\sqrt { v_1^2+ 2gh } \)
\( v_2=\sqrt { (2м/с)^2+ 2 \cdot 10м/с^2 \cdot 2,25 м }=7 м/с \)
Ответ: \(v_2=7 м/с \)
Задача 11
Мальчик подъезжает на самокате к подъему, скорость мальчика в начале подъема \( v_1=9 м/с. \)
Высота подъема \(h=3,6 м .\)
Найти скорость мальчика в конце подъема.
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v_1=9 м/с \)
\( g=10м/с^2 \; \)
\( h=3,6 м \)
\(v_2-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+0 = E_{к2}+mgh \)
\( \dfrac{ mv_1^2}{2}=\dfrac{ mv_2^2}{2}+ mgh \)
\( mv_1^2= mv_2^2 + 2mgh \)
\( v_1^2= v_2^2 + 2gh \)
\( v_2^2= v_1^2 - 2gh \)
\( v_2= \sqrt { v_1^2 - 2gh } \)
\( v_2=\sqrt { (9м/с)^2- 2 \cdot 10м/с^2 \cdot 3,6 м }=3 м/с \)
Ответ: \(v_2=3 м/с \)
Задача 12
Мяч бросают с высоты \(h_1= 11м \) вертикально вниз со скоростью \(v= 10 м/с ,\) после чего он абсолютно упруго
отталкивается от пола и летит вверх.
На какую максимальную высоту поднимется мяч?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v=10 м/с \)
\( g=10м/с^2 \; \)
\( h_1= 11м \)
\(h_2-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv^2}{2}+mgh_1 = 0+mgh_2 \)
\( mv^2+2mgh_1 = 2mgh_2 \)
\( v^2+2gh_1 = 2gh_2 \)
\( h_2 = \dfrac{ v^2+2gh_1 }{2g} \)
\( h_2 = \dfrac{ (10м/с)^2+2\cdot 10м/с^2 \cdot 11м }{2\cdot 10м/с^2} =16м \)
Ответ: \( h_2 = 16м \)
Задача 13
Мяч бросают с высоты \(h_1= 10м \) вертикально вниз со скоростью \(v= 10 м/с ,\) после чего он абсолютно упруго
отталкивается от пола и летит вверх.
Найти скорость мяча на высоте \(h_2= 14,2м \)
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v_1=10 м/с \)
\( g=10м/с^2 \; \)
\( h_1=10 м \)
\( h_2=14,2 м \)
\(v_2-? \)
Перепишем уравнение закона сохранения энергии:
\( E_{к1}+E_{п1}=E_{к2}+E_{п2} \)
\( \dfrac{ mv_1^2}{2}+mgh_1 = \dfrac{ mv_2^2}{2} +mgh_2 \)
\( mv_1^2+2mgh_1 = mv_2^2 +2mgh_2 \)
\( v_1^2+2gh_1 = v_2^2 +2gh_2 \)
\( v_1^2+2gh_1 -2gh_2 = v_2^2 \)
\(v_2^2 = v_1^2+2gh_1 -2gh_2 \)
\(v_2 = \sqrt { v_1^2+2gh_1 -2gh_2 } \)
\(v_2 = \sqrt { (10 м/с) ^2+ 2 \cdot 10м/с^2 \cdot 10м -2 \cdot 10м/с^2 \cdot 14,2 м }=4 м/с \)
Ответ: \(v_2=4 м/с \)
Задача 16
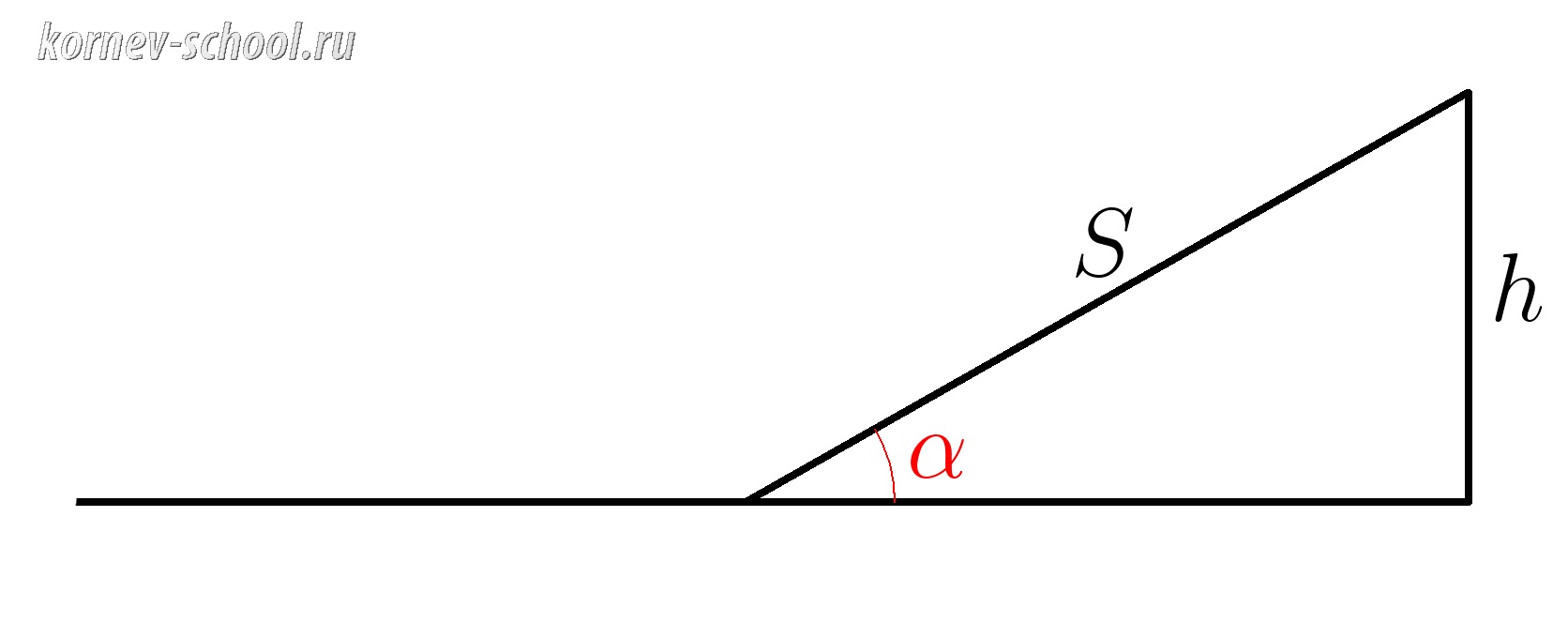
Велосипедист движется по горизонтальному участку велосипедного полигона с постоянной скоростью \(v= 11 м/с .\)
Впереди высокий трамплин с углом наклона \(\alpha =30^0 \), какое расстояние \(S\) проедет
велосипедист по трамплину, если не будет крутить педали?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v=11 м/с \)
\( g=10м/с^2 \; \)
\( \alpha = 30^0 \)
\(S-? \)
Составим уравнение закона сохранения энергии:
\( \dfrac{ mv^2}{2} = mgh\)
\( sin \; \alpha= \dfrac{h}{S} \)
\(h= S \cdot sin \; \alpha \)
\( \dfrac{ mv^2}{2} = mg S \cdot sin \; \alpha \)
\( mv^2 = 2mg S \cdot sin \; \alpha \)
\( v^2 = 2g S \cdot sin \; \alpha \)
\( S = \dfrac{ v^2}{2 g sin \; \alpha} \)
\( S = \dfrac{ (11 м/с)^2 }{2 \cdot 10м/с^2 \cdot sin \; 30^0} =12,1м \)
Ответ: \( S =12,1м \)
Задача 17

Автомобиль с заглохшим двигателем движется по горизонтальному участку со скоростью \( v=25 м/с \)
и заезжает на затяжной подъем с углом
наклона \(\alpha =30^0 .\)
Какое расстояние проедет автомобиль по инерции?
\( g=10м/с^2 \; \)
Показать ответ
Показать решение
Видеорешение
Дано:
\( v=25 м/с \)
\( g=10м/с^2 \; \)
\( \alpha = 30^0 \)
\(S-? \)
Составим уравнение закона сохранения энергии:
\( \dfrac{ mv^2}{2} = mgh\)
\( sin \; \alpha= \dfrac{h}{S} \)
\(h= S \cdot sin \; \alpha \)
\( \dfrac{ mv^2}{2} = mg S \cdot sin \; \alpha \)
\( mv^2 = 2mg S \cdot sin \; \alpha \)
\( v^2 = 2g S \cdot sin \; \alpha \)
\( S = \dfrac{ v^2}{2 g sin \; \alpha} \)
\( S = \dfrac{ (25 м/с)^2 }{2 \cdot 10м/с^2 \cdot sin \; 30^0} =62,5м \)
Ответ: \( S =62,5м \)
Пройти тест на эту тему (10 задач)

